To save time, it is sometimes useful to find the LCM and GCF of two or more numbers simultaneously. Here are two ways to do this.
This method consists of simultaneously dividing the numbers whose LCM and GCF are desired by prime numbers. This method is useful for finding the LCM and the GCF of two larger numbers.
-
Draw a table with the first column titled Prime factors. The labels of the other columns are the numbers whose LCM and GCF must be found.
-
Try to divide the numbers by prime factors. If one of these numbers cannot be divided evenly by a prime factor, write a dash (hyphen) in the appropriate cell. Continue dividing until there is a |1| in each column.
-
Calculate the LCM by multiplying all the prime factors in the first column.
-
Calculate the GCF by multiplying the common prime factors in the first column (only those in rows without a dash).
Calculate the LCM and the GCF of |40| and |48|.
-
Draw a table with the first column titled Prime factors. The labels of the other columns are the numbers whose LCM and GCF must be found.
|
Prime Factors |
|40| |
|48| |
|---|---|---|
|
... |
... |
... |
-
Try to divide the given numbers by prime factors. If one of these numbers cannot be divided evenly by a prime factor, write a dash (hyphen) in the appropriate cell. Continue dividing until there is a |1| in each column.
|
Prime factors |
|40| |
|48| |
|---|---|---|
|
|\color{blue}{2}| |
|20| |
|24| |
|
|\color{blue}{2}| |
|10| |
|12| |
|
|\color{blue}{2}| |
|5| |
|6| |
|
|\color{blue}{2}| |
|-| |
|3| |
|
|\color{blue}{3}| |
|-| |
|1| |
|
|\color{blue}{5}| |
|1| |
|-| |
-
Calculate the LCM by multiplying all the prime divisors in the first column
||\begin{align} LCM(40,48)&=\color{blue}{2}\times\color{blue}{2}\times \color{blue}{2}\times\color{blue}{2}\times \color{blue}{3}\times \color{blue}{5}\\&=240\end{align}|| -
Calculate the GCF by multiplying the common prime factors in the first column (only those in rows without a dash)
|
Prime factors |
|40| |
|48| |
|---|---|---|
|
|\color{#3a9a38}{\boldsymbol{2}}| |
|20| |
|24| |
|
|\color{#3a9a38}{\boldsymbol{2}}| |
|10| |
|12| |
|
|\color{#3a9a38}{\boldsymbol{2}}| |
|5| |
|6| |
|
|\color{blue}{2}| |
|-| |
|3| |
|
|\color{blue}{3}| |
|-| |
|1| |
|
|\color{blue}{5}| |
|1| |
|-| |
|\begin{align} GCF(40,48)&=\color{#3a9a38}{2}\times \color{#3a9a38}{2}\times \color{#3a9a38}{2}\\ &=8\end{align}|
Calculate the LCM and GCF of |12,| |54,| and |210.|
-
Draw a table with the first column titled Prime factors. The labels of the other columns are the numbers whose LCM and GCF must be found.
|
Prime factors |
|12| |
|54| |
|210| |
|---|---|---|---|
|
... |
... |
... |
... |
-
Try to divide the given numbers by prime factors. If any of these numbers cannot be divided evenly by a prime factor, write a dash (hyphen) in the appropriate cell. Continue dividing until there is a |1| in each column.
|
Prime factors |
|12| |
|54| |
|210| |
|---|---|---|---|
|
|\color{blue}{2}| |
|6| |
|27| |
|105| |
|
|\color{blue}{2}| |
|3| |
|-| |
|-| |
|
|\color{blue}{3}| |
|1| |
|9| |
|35| |
|
|\color{blue}{3}| |
|-| |
|3| |
|-| |
|
|\color{blue}{3}| |
|-| |
|1| |
|-| |
|
|\color{blue}{5}| |
|-| |
|-| |
|7| |
|
|\color{blue}{7}| |
|-| |
|-| |
|1| |
-
Calculate the LCM by multiplying all the prime factors in the first column
||\begin{align} LCM(12,54,210)&=\color{blue}{2}\times\color{blue}{2}\times \color{blue}{3}\times\color{blue}{3}\times \color{blue}{3}\times \color{blue}{5}\times \color{blue}{7}\\&=3780\end{align}|| -
Calculate the GCF by multiplying the common prime factors in the first column (only those in rows without a dash)
|
Prime factors |
|12| |
|54| |
|210| |
|---|---|---|---|
|
|\color{#3a9a38}{\boldsymbol{2}}| |
|6| |
|27| |
|105| |
|
|\color{blue}{2}| |
|3| |
|-| |
|-| |
|
|\color{#3a9a38}{\boldsymbol{3}}| |
|1| |
|9| |
|35| |
|
|\color{blue}{3}| |
|-| |
|3| |
|-| |
|
|\color{blue}{3}| |
|-| |
|1| |
|-| |
|
|\color{blue}{5}| |
|-| |
|-| |
|7| |
|
|\color{blue}{7}| |
|-| |
|-| |
|1| |
|\begin{align} GCF(12,54,210)&=\color{#3a9a38}{2}\times \color{#3a9a38}{3}\\ &=6\end{align}|
This multipurpose method consists of making a factor tree for each of the numbers and then placing the prime factors in a Venn diagram in order to determine the LCM and the GCF.
-
Decompose each number into a product of its prime factors using a factor tree (prime factorization).
-
Draw a Venn diagram that includes a circle for each of the numbers whose LCM and GCF are sought. Place the prime factors obtained in step 1 in the Venn diagram according to whether they are shared by all numbers, common to only some numbers, or unique.
-
Calculate the LCM by multiplying all the prime factors present in the Venn diagram.
-
Calculate the GCF by multiplying only the prime factors common to all the numbers.
Find the LCM and GCF of |156| and |182|.
-
Decompose each number into a product of its prime factors using a factor tree (prime factorization)
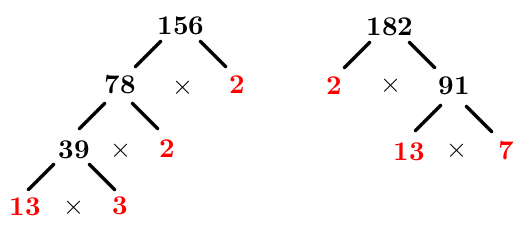
The prime factorizations are:
|\begin{align}156&=2\times 2\times 3\times 13\\
182&=2\times 7\times 13\end{align}|
-
Draw a Venn diagram that includes a circle for each of the numbers whose LCM and GCF are sought. Place the prime factors obtained in step 1 in the Venn diagram according to whether they are shared by all numbers, common to only some numbers, or unique.
The prime factorizations are the following:
|\begin{align}156&=\color{blue}{2}\times \color{green}{2}\times \color{green}{3}\times \color{blue}{13}\\
182&=\color{blue}{2}\times \color{green}{7}\times \color{blue}{13}\end{align}|
This results in the following Venn diagram.
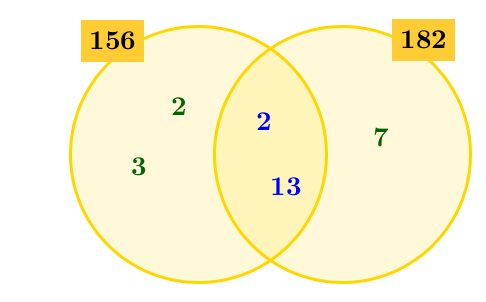
-
Calculate the LCM by multiplying all the prime factors present in the Venn diagram.
|\begin{align}LCM(156,182)&=2\times 3\times 2\times 13\times 7\\ &=1092\end{align}| -
Calculate the GCF by multiplying only the prime factors common to all the numbers.
|\begin{align}GCF(156,182)&=2\times 13\\ &=26\end{align}|
Calculate the LCM and GCF of |72|, |90|, and |315|.
-
Decompose each number into a product of its prime factors using a factor tree (prime factorization)
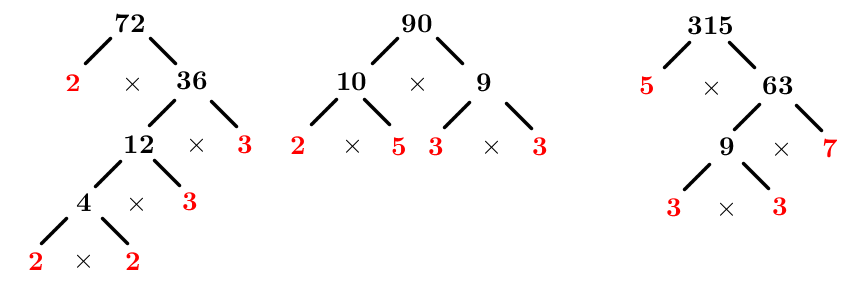
The prime factorizations are:
|\begin{align}72&=2\times 2\times 2\times 3\times 3\\
90&=2\times 3\times 3\times 5\\
315&=3\times 3\times 5\times 7\end{align}|
-
Draw a Venn diagram that includes a circle for each of the numbers whose LCM and GCF are sought. Place the prime factors obtained in step 1 in the Venn diagram according to whether they are shared by all numbers, common to only some numbers, or unique.
The prime factorizations are the following:
|\begin{align}72&=\color{purple}{2}\times \color{green}{2}\times \color{green}{2}\times \color{blue}{3}\times\color{blue}{3}\\
90&=\color{purple}{2}\times\color{blue}{3}\times\color{blue}{3}\times \color{purple}{5}\\
315&=\color{blue}{3}\times\color{blue}{3}\times \color{purple}{5}\times \color{green}{7}\end{align}|
This results in the following Venn diagram.
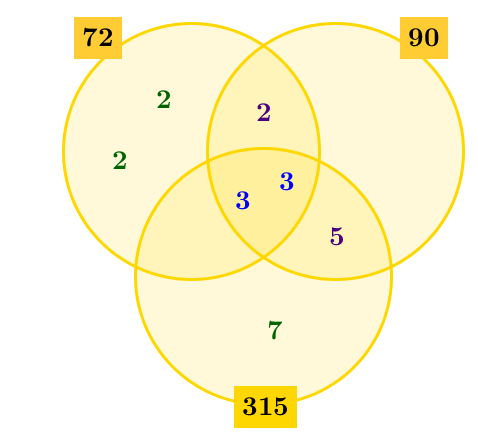
-
Calculate the LCM by multiplying all the prime factors present in the Venn diagram.
|\begin{align}LCM(72,90,315)&=2\times 2\times 2\times 3\times 3\times 5\times 7\\ &=2520\end{align}| -
Calculate the GCF by multiplying only the prime factors common to all the numbers.
|\begin{align}GCF(72,90,315)&=3\times 3\\ &=9\end{align}|