Code de contenu
m1545
Slug (identifiant)
les-methodes-pour-trouver-le-ppcm-et-le-pgcd-simu
Contenu parent
Les diviseurs, les multiples et la factorisation
Niveaux
Secondaire 1
Secondaire 2
Matière
Mathématiques
Tags
premiers
diviseurs
facteurs
PGCD
PPCM
facteurs premiers
PPCM et PGCD
méthodes
calculer PPCM
calculer PGCD
plus grand commun diviseur
plus grand commun multiple
Contenu
Contenu
Corps

Pour sauver du temps, il est parfois utile de trouver le PPCM et le PGCD de 2 ou plusieurs nombres simultanément. Voici 2 méthodes permettant d'y arriver :

Liens
Type
Ancre
Titre
Méthode 1 : le tableau de diviseurs
Ancre
methode-1-le-tableau-de-diviseurs
Type
Ancre
Titre
Méthode 2 : l'arbre de facteurs et le diagramme
Ancre
methode-2-l-arbre-des-facteurs-et-le-diagramme
Titre (niveau 2)
Méthode 1 : le tableau de diviseurs
Slug (identifiant) du title
methode-1-le-tableau-de-diviseurs
Contenu
Corps

Cette méthode consiste à diviser simultanément par des nombres premiers les nombres dont on cherche le PPCM et le PGCD. Cette méthode s'avère pratique lorsque l'on cherche le PPCM et le PGCD entre 2 grands nombres.

Sur-titre
Règle
Contenu
Corps

  1. Tracer un tableau dont le titre de la 1re colonne sera Diviseurs premiers. Les titres des autres colonnes seront les nombres étudiés.

  2. Tenter de diviser les nombres étudiés par des diviseurs premiers. Si un des nombres ne se divise pas par le diviseur premier utilisé, on inscrit un trait dans la case appropriée. On poursuit les divisions jusqu'à ce qu'on obtienne |1| dans chaque colonne.

  3. Calculer le PPCM en multipliant tous les diviseurs premiers de la 1re colonne.

  4. Calculer le PGCD en multipliant seulement les diviseurs premiers des lignes pleines (les lignes sans trait).

Contenu
Corps

Calculer le PPCM et le PGCD de |40| et |48.|

  1. Tracer un tableau dont le titre de la 1re colonne sera Diviseurs premiers. Les titres des autres colonnes seront les nombres étudiés.

Diviseurs
premiers		 |40| |48|
... ... ...

  1. Tenter de diviser les nombres étudiés par des diviseurs premiers. Si un des nombres ne se divise pas par le diviseur premier utilisé, on inscrit un trait dans la case appropriée. On poursuit les divisions jusqu'à ce qu'on obtienne |1| dans chaque colonne.

Diviseurs
premiers		 |40| |48|
|\color{#3b87cd}{2}| |20| |24|
|\color{#3b87cd}{2}| |10| |12|
|\color{#3b87cd}{2}| |5| |6|
|\color{#3b87cd}{2}| |-| |3|
|\color{#3b87cd}{3}| |-| |1|
|\color{#3b87cd}{5}| |1| |-|

  1. Calculer le PPCM en multipliant tous les diviseurs premiers de la 1re colonne ||\begin{align} PPCM(40,48)&=\color{#3b87cd}{2}\times\color{#3b87cd}{2}\times \color{#3b87cd}{2}\times\color{#3b87cd}{2}\times \color{#3b87cd}{3}\times \color{#3b87cd}{5}\\&=240\end{align}||

  2. Calculer le PGCD en multipliant seulement les diviseurs premiers des lignes pleines (les lignes sans trait)

Nombre de colonnes
2 colonnes
Format
50% / 50%
Première colonne
Corps
Diviseurs
premiers		 |40| |48|
|\color{#3a9a38}{\boldsymbol{2}}| |20| |24|
|\color{#3a9a38}{\boldsymbol{2}}| |10| |12|
|\color{#3a9a38}{\boldsymbol{2}}| |5| |6|
|\color{#3b87cd}{2}| |-| |3|
|\color{#3b87cd}{3}| |-| |1|
|\color{#3b87cd}{5}| |1| |-|
Deuxième colonne
Corps

|\begin{align} PGCD(40,48)&=\color{#3a9a38}{2}\times \color{#3a9a38}{2}\times \color{#3a9a38}{2}\\ &=8\end{align}|

Contenu
Corps

Calculer le PPCM et le PGCD de |12,| |54| et |210.|

  1. Tracer un tableau dont le titre de la 1re colonne sera Diviseurs premiers. Les titres des autres colonnes seront les nombres étudiés.

Diviseurs
premiers		 |12| |54| |210|
... ... ... ...

  1. Tenter de diviser les nombres étudiés par des diviseurs premiers. Si un des nombres ne se divise pas par le diviseur premier utilisé, on inscrit un trait dans la case appropriée. On poursuit les divisions jusqu'à ce qu'on obtienne |1| dans chaque colonne.

Diviseurs
premiers		 |12| |54| |210|
​|\color{#3b87cd}{2}| |6| |27| |105|
​|\color{#3b87cd}{2}| |3| |-| |-|
​|\color{#3b87cd}{3}| |1| |9| |35|
​|\color{#3b87cd}{3}| |-| |3| |-|
​|\color{#3b87cd}{3}| |-| |1| |-|
​|\color{#3b87cd}{5}| |-| |-| |7|
​|\color{#3b87cd}{7}| |-| |-| |1|

  1. Calculer le PPCM en multipliant tous les diviseurs premiers de la 1re colonne ||\begin{align} PPCM(12,54,210)&=\color{#3b87cd}{2}\times\color{#3b87cd}{2}\times \color{#3b87cd}{3}\times\color{#3b87cd}{3}\times \color{#3b87cd}{3}\times \color{#3b87cd}{5}\times \color{#3b87cd}{7}\\&=3\ 780\end{align}||

  2. Calculer le PGCD en multipliant seulement les diviseurs premiers des lignes pleines (les lignes sans trait)

Nombre de colonnes
2 colonnes
Format
50% / 50%
Première colonne
Corps
Diviseurs
premiers		 |12| |54| |210|
​|\color{#3a9a38}{\boldsymbol{2}}| |6| |27| |105|
​|\color{#3b87cd}{2}| |3| |-| |-|
​|\color{#3a9a38}{\boldsymbol{3}}| |1| |9| |35|
​|\color{#3b87cd}{3}| |-| |3| |-|
​|\color{#3b87cd}{3}| |-| |1| |-|
​|\color{#3b87cd}{5}| |-| |-| |7|
​|\color{#3b87cd}{7}| |-| |-| |1|
Deuxième colonne
Corps

|\begin{align} PGCD(12,54,210)&=\color{#3a9a38}{2}\times \color{#3a9a38}{3}\\ &=6\end{align}|

Titre (niveau 2)
Méthode 2 : L'arbre des facteurs et le diagramme
Slug (identifiant) du title
methode-2-l-arbre-des-facteurs-et-le-diagramme
Contenu
Corps

Cette méthode consiste à construire l'arbre des facteurs pour chacun des nombres étudiés et à placer les facteurs premiers dans un diagramme de Venn afin de déterminer le PPCM et le PGCD. Cette méthode est très polyvalente.

Sur-titre
Règle
Contenu
Corps

  1. Décomposer chaque nombre en produit de facteurs premiers à l'aide de l'arbre de facteurs.

  2. Tracer un diagramme de Venn comprenant un ensemble pour chaque nombre étudié et placer les facteurs premiers trouvés à l'étape 1 selon s'ils sont communs à tous les nombres, communs à certains nombres seulement ou uniques.

  3. Calculer le PPCM en multipliant tous les facteurs premiers présents dans le diagramme de Venn.

  4. Calculer le PGCD en multipliant seulement les facteurs premiers communs à tous les nombres.

Contenu
Corps

Détermine le PPCM et le PGCD de |156| et |182.|

  1. Décomposer chaque nombre en produit de facteurs premiers à l'aide de l'arbre de facteurs

Image
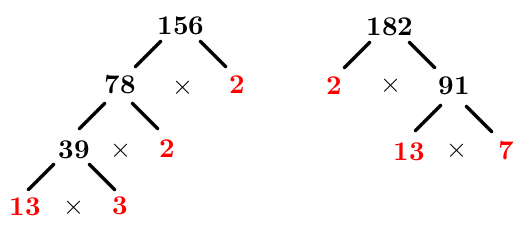
Les arbres de facteurs premiers de 156 et 182.
Corps

On obtient ceci. ||\begin{align}156&=2\times 2\times 3\times 13\\
182&=2\times 7\times 13\end{align}||

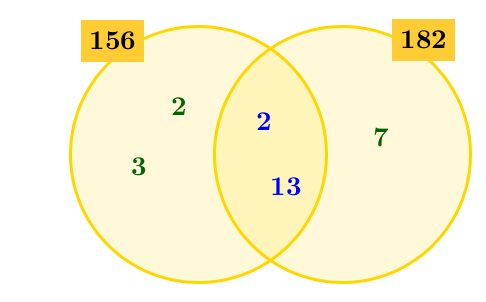
  1. Tracer un diagramme de Venn comprenant un ensemble pour chaque nombre étudié et placer les facteurs premiers trouvés à l'étape 1 selon s'ils sont communs à tous les nombres, communs à certains nombres seulement ou uniques.

    On a ceci. ||\begin{align}156&=\color{#333fb1}{2}\times \color{#3a9a38}{2}\times \color{#3a9a38}{3}\times \color{#333fb1}{13}\\182&=\color{#333fb1}{2}\times \color{#3a9a38}{7}\times \color{#333fb1}{13}\end{align}||On obtient le diagramme de Venn suivant.

Image
Diagramme de Venn montrant les facteurs premiers de 156 et 182.
Corps

  1. Calculer le PPCM en multipliant tous les facteurs premiers présents dans le diagramme de Venn ||\begin{align}PPCM(156,182)&=\color{#3a9a38}{2}\times \color{#3a9a38}{3}\times \color{#333fb1}{2}\times \color{#333fb1}{13}\times \color{#3a9a38}{7}\\ &=1\ 092\end{align}||

  2. Calculer le PGCD en multipliant seulement les facteurs premiers communs à tous les nombres ||\begin{align}PGCD(156,182)&=\color{#333fb1}{2}\times \color{#333fb1}{13}\\ &=26\end{align}||

Contenu
Corps

Calcule le PPCM et le PGCD de |72,| |90| et |315.|

  1. Décomposer chaque nombre en produit de facteurs premiers à l'aide de l'arbre de facteurs

Image
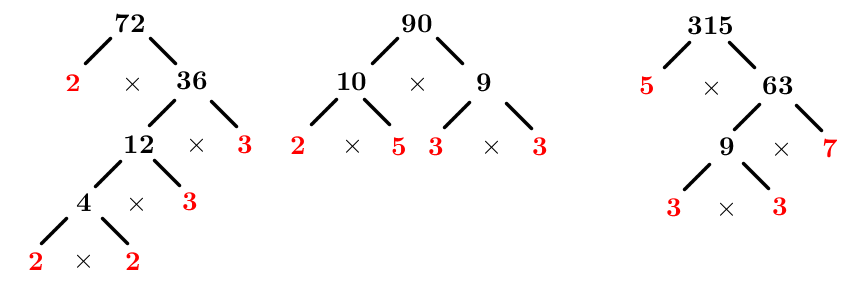
Les arbres de facteurs premiers de 72, 90 et 315.
Corps

On obtient ceci. ||\begin{align}72&=2\times 2\times 2\times 3\times 3\\90&=2\times 3\times 3\times 5\\315&=3\times 3\times 5\times 7\end{align}||

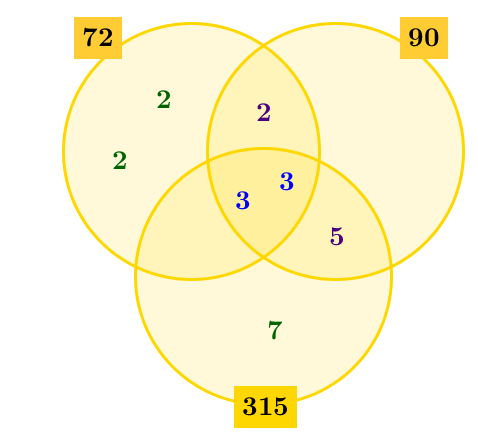
  1. Tracer un diagramme de Venn comprenant un ensemble pour chaque nombre étudié et placer les facteurs premiers trouvés à l'étape 1 selon s'ils sont communs à tous les nombres, communs à certains nombres seulement ou uniques.

    On a ceci. ||\begin{align}72&=\color{purple}{2}\times \color{green}{2}\times \color{green}{2}\times \color{blue}{3}\times\color{blue}{3}\\90&=\color{purple}{2}\times\color{blue}{3}\times\color{blue}{3}\times \color{purple}{5}\\315&=\color{blue}{3}\times\color{blue}{3}\times \color{purple}{5}\times \color{green}{7}\end{align}||On obtient le diagramme de Venn suivant.

Image
image
Corps

  1. Calculer le PPCM en multipliant tous les facteurs premiers présents dans le diagramme de Venn ||\begin{align}PPCM(72,90,315)&=\color{#3a9a38}{2}\times \color{#3a9a38}{2}\times \color{#560fa5}{2}\times \color{#333fb1}{3}\times \color{#333fb1}{3}\times \color{#560fa5}{5}\times \color{#3a9a38}{7}\\ &=2\ 520\end{align}||

  2. Calculer le PGCD en multipliant seulement les facteurs premiers communs à tous les nombres ||\begin{align}PGCD(72,90,315)&=\color{#333fb1}{3}\times \color{#333fb1}{3}\\ &=9\end{align}||

Retirer la lecture audio
Non