Ordering Irrational Numbers

• Placing the numbers in ascending order is equivalent to ordering the numbers from smallest to largest according to their value.

• Placing numbers in descending order is the same as ordering numbers from largest to smallest according to their value.

1. Determine whether to place the numbers in ascending or descending order.

2. Express irrational numbers in decimal notation using a calculator.

3. Keep as many decimal places as needed to compare numbers when rounding.

4. Place the numbers obtained in step 3 on a number line.

5. Place the numbers in the desired order, expressing them in their original form.

Place the following irrational numbers in ascending order. ||\sqrt{2}\qquad \pi\qquad \sqrt{3}\qquad -\dfrac{\pi}{2}\qquad -\dfrac{\pi}{3}\qquad -\dfrac{\sqrt{10}}{2}||

1. Determine whether to place the numbers in ascending or descending order
   As mentioned in the statement, the numbers should be placed in ascending order from smallest to largest.

2. Express irrational numbers in decimal notation using a calculator
   ||\begin{align} \sqrt{2}&=1.414213... & &\qquad & \dfrac{\pi}{4}&=0.785398...\\ \\\sqrt{3}&=1.732050... & &\qquad & -\dfrac{\pi}{2}&=-1.570796...\\ \\ -\dfrac{\pi}{3}&=-1.047197... & &\qquad & -\dfrac{\sqrt{10}}{2}&=-1.581138...\end{align}||

3. Keep as many decimal places as needed to compare numbers when rounding
   We can keep three decimal places by rounding to thousandths.
   ||\begin{align} \sqrt{2}&\approx1.414 & &\qquad & \dfrac{\pi}{4}&\approx0.785\\ \\ \sqrt{3}&\approx1.732 & &\qquad & -\dfrac{\pi}{2}&\approx-1.571\\ \\ -\dfrac{\pi}{3}&\approx-1.047 & &\qquad & -\dfrac{\sqrt{10}}{2}&\approx-1.581\end{align}||

4. Position the numbers on a number line using the values obtained in step 3

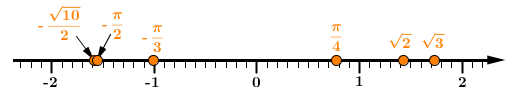
5. Place the numbers in the desired order, expressing them in their original form
   The following ascending order is obtained. ||-\dfrac{\sqrt{10}}{2}\ <\ -\dfrac{\pi}{2}\ <\ -\dfrac{\pi}{3}\ <\ \dfrac{\pi}{4}\ <\ \sqrt{2}\ <\ \sqrt{3}||