The set of irrational numbers, represented by |\mathbb{R}\backslash\mathbb{Q}| or |\mathbb{Q}’,| includes all numbers that are not a ratio of 2 integers.
These numbers have an infinite, non-periodic decimal expansion.
Rational numbers |(\mathbb{Q}),| or numbers that can be expressed as a ratio of integers, have either finite decimal expansions or infinite, periodic decimal expansions. Irrational numbers, however, have an infinite, non-periodic decimal expansion.
Finite decimal expansion
The number |\dfrac{7}{4}| is rational. Dividing the numerator by the denominator of this fraction gives the decimal number |1.75.|
The decimal expansion of this number ends at |5.| We therefore say that |\dfrac{7}{4}| has a finite decimal expansion.||\dfrac{7}{4}=1.75||
Infinite and periodic decimal expansion
The number |\dfrac{58}{11}| is rational. Dividing the numerator by the denominator of this fraction gives the decimal number |5.272727272\dots|
The decimal expansion of this number is composed of the digits |2| and |7,| which repeat infinitely. This is known as the period. We therefore say that |\dfrac{58}{11}| has an infinite, periodic decimal expansion.||\dfrac{58}{11}=5.\overline{27}||
Infinite and non-periodic decimal expansion
The number |\pi| is irrational. This means that there is no fraction that corresponds to the exact value of |\pi| when the numerator is divided by the denominator. Its value, in decimal notation, is |3.141592653\dots|
The decimal expansion of this number is non-repeating and never ends. We therefore say that |\pi| has an infinite, non-periodic decimal expansion.||\pi\approx 3.141592653\dots||
The set of irrational numbers, denoted |\mathbb{R}\backslash\mathbb{Q}| or |\mathbb{Q}’,| and the set of rational numbers, denoted |\mathbb{Q},| are mutually exclusive, meaning that a number cannot be both rational and irrational. We may use the following notation to represent the relationship between these sets.||\mathbb{Q}\cap\mathbb{Q'}=\varnothing||This is read as: "The intersection of the set of rational numbers and the set of irrational numbers corresponds to the empty set."
Furthermore, when we combine the set of rational numbers and the set of irrational numbers, we get the set of real numbers.||\mathbb{Q}\cup\mathbb{Q'}=\mathbb{R}||
This reads as: "The union of rational and irrational numbers corresponds to the set of real numbers." In other words, the set of rational numbers and the set of irrational numbers are complementary.
Here's a diagram showing the position of irrational numbers in the set of real numbers.
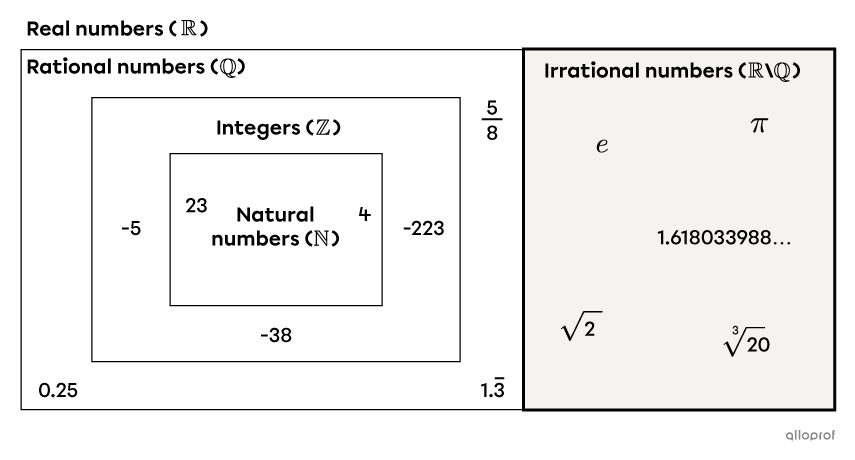
-
The number |\pi,| the Euler number |(e)| and the golden ratio |(\varphi)| are irrational numbers, because their decimal expansion is infinite and non-periodic.||\begin{align}\pi&\approx 3.141592653\dots\\ e&\approx 2.718281828\dots\\ \varphi&\approx 1.618033988\dots\end{align}||
-
The numbers |\sqrt{5}| and |-\sqrt[3]{12}| are irrational numbers because they cannot be expressed as a ratio of integers.
-
The number |-\sqrt{16}| is not an irrational number; rather, it belongs to the set of integers because it corresponds to the number |-4.|
-
The number |\sqrt{5.76}| is not irrational; instead, it belongs to the set of rational numbers, because it corresponds to the number |2.4.|
-
The number |3.456456456\dots| is not an irrational number. This is because there is a period in this number: the digits |456| repeat. Since it contains a period, |3.\overline{456}| is a rational number and can be expressed as a fraction.
-
Using the appropriate notation, we get the following:||\begin{align}\sqrt{5}&\in\mathbb{R}\backslash\mathbb{Q}\\ 3.\overline{456}&\notin\mathbb{R}\backslash\mathbb{Q}\end{align}||
-
We denote |(\mathbb{R}\backslash\mathbb{Q})_+| or |\mathbb{Q}'_{\,+}| the set of positive irrational numbers.
-
We denote |(\mathbb{R}\backslash\mathbb{Q})_-| or |\mathbb{Q}'_{\,-}| the set of negative irrational numbers.
To order irrational numbers, it is useful to convert them into decimal notation.