In the following animation, select a sinusoidal function (sine or cosine), and then experiment with its parameters |a,| |b,| |h,| and |k|. Observe their effects on the function’s properties. After experimenting, read the concept sheet for more details concerning the properties of these functions.
The following table provides an analysis of all the properties of the sine function along with examples.
|
Properties |
Standard Equation |
Example |
|---|---|---|
|
Formula |
|f(x)=a\sin(b(x-h))+k| |
|f(x)=-4\sin(-2(x-\pi))+3| |
|
Midline |
|y=k| |
|y=3| |
|
Period |
|P=\dfrac{2 \pi}{\mid b \mid }| |
|P=\dfrac{2\pi}{\mid -2 \mid}=\pi| |
|
Domain |(\text{dom }f)| |
|\text{dom }f=\mathbb{R}| |
|\text{dom } f=\mathbb{R}| |
|
Range |(\text{ran }f)| |
|\text{ran } f = [k\ -\mid a \mid ,\ k\ +\mid a \mid]| |
|[-1,\ 7]| |
|
Variation |
1|P| is the period where |n \in \mathbb{Z}.| |
Since |a| and |b| have the same sign, the function increases as it passes through the point |(\pi,3).| The function increases over the interval ||\left[\dfrac{3\pi}{4}+n\pi,\ \dfrac{5\pi}{4}+n\pi\right],|| The function decreases over the interval ||\left[\dfrac{5\pi}{4}+n\pi,\ \dfrac{7\pi}{4}+n\pi\right],||
|
|
Zeros of the Function |
These are the values of |x| for which |f(x)=0.| |
|x=5{.}13+n\pi| |
|
y-Intercept |
This is the value of |f(0)| |
|f(0)=3| |
|
Sign |
The intervals where the function is positive and negative depend on the zeros of the function, the period, and the shape of the graph. |
The function is negative on the intervals |[5{.}13+n\pi,\ 5{.}85+n\pi]| where |n\in\mathbb{Z}.| The function is positive on the intervals |[5{.}85+n\pi,\ 8{.}28+n\pi]| where |n\in\mathbb{Z}.| |
|
Extrema |
Maximum: |k\ + \mid a\ \mid| Minimum: |k\ - \mid a\ \mid| |
Maximum: |7| Minimum: |-1| |
Determine the properties of the following sine function: ||f(x)=-1{.}5\sin\left(2\left(x-\frac{3\pi}{4}\right)\right)+1||
It may be useful to plot the graph of the function.
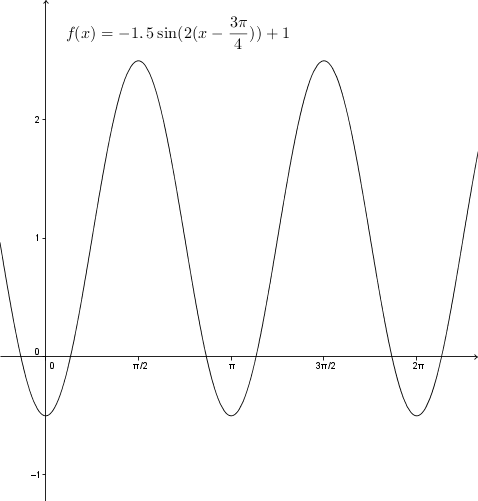
-
The equation for the axis of oscillation is |y=1.|
-
The parameter |b| is equal to 2, therefore the period of the function is |\displaystyle P = \frac{2\pi}{\mid b \mid} = \frac{2\pi}{\mid 2 \mid} = \pi.|
-
The domain of the function is the set of real numbers, i.e., |\mathbb{R}.|
-
The range of the function is an interval of the form |[k\ -\mid a \mid,\ k\ + \mid a \mid ].|
Here, |a=-1{.}5| and |k=1,| so the range is the interval |[-0{.}5;\ 2{.}5].| -
The variation: since the parameters |a| and |b| have opposite signs, the curve decreases when it passes through the point of inflection |(h,k)= \left(\dfrac{3\pi}{4}, 1\right).|
-
The function decreases over the interval |\left[h-\frac{1}{4}P+nP,\ h+\frac{1}{4}P+nP\right].|
Replacing |h| with |\dfrac{3\pi}{4}| and |P| by |\pi| gives the following interval: ||\left[\frac{\pi}{2} + n \pi,\ \pi +n \pi \right]|| where |n \in \mathbb{Z}| -
It increases over the interval |\left[h+\frac{1}{4}P+nP,\ h+\frac{3}{4}P+nP \right].|
Replacing |h| by |\dfrac{3\pi}{4}| and |P| by |\pi| gives the following interval: ||\left[\pi + n \pi,\ \frac{3 \pi}{2}+n\pi \right]|| where |n \in \mathbb{Z}|
-
-
The zeros of the function are calculated by replacing |f(x)| by |0.| ||\begin{align}0 &= -1{.}5\sin\left(2\left(x-\frac{3\pi}{4}\right)\right)+1\\-1 &= -1{.}5 \sin\left(2\left(x-\frac{3\pi}{4}\right)\right)\\ \frac{-1}{-1{.}5} &= \frac{2}{3} = \sin\left(2\left(x-\frac{3\pi}{4}\right)\right)\end{align}||Now, refer to the unit circle to find the points where sine is |\dfrac{2}{3}.|
The first value corresponds to approximately |0{.}73| radians, because |\sin^{-1}\left(\dfrac{2}{3}\right)\approx 0{.}73.|
Draw a unit circle for the second value.
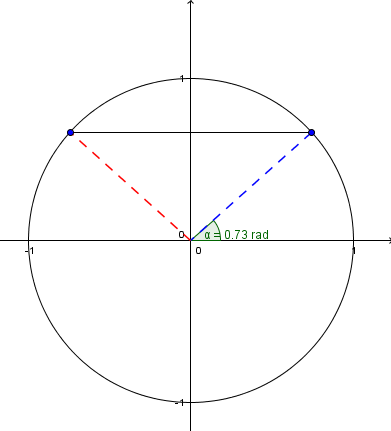
The second value corresponds to the angle between the |x|-axis and the dotted red line. Use |\pi - 0{.}73 \approx 2{.}41| radians to calculate this value.
The solution is not yet finished since these two values correspond to the value of the angle in sine, i.e., ||2\left(x-\frac{3\pi}{4}\right)=0{.}73\text{ radian }\\ \text{and}\\ 2\left(x-\frac{3\pi}{4}\right)=2{.}41\text{ radians}|| It is still necessary to isolate |x| in both equations.
In the first case : ||\begin{align}2\left(x-\frac{3\pi}{4}\right)&=0{.}73\\x-\frac{3\pi}{4} &= 0{.}365\\x &= 0{.}365 + \frac{3\pi}{4}\\x_1 &\approx 2{.}72\end{align}||In the second case : ||\begin{align}2\left(x-\frac{3\pi}{4}\right) &= 2{.}41\\x - \frac{3\pi}{4} &= 1{.}205\\x &= 1{.}205 + \frac{3\pi}{4}\\ x_2 &\approx 3{.}56\end{align}||Thus, the general expression which gives the zeros is: ||\lbrace 2{.}72 + n \pi \rbrace \cup \lbrace 3{.}56 + n \pi \rbrace \text{ where } n \in \mathbb{Z}||
-
To calculate the y-intercept, replace |x| by |0.| ||\begin{align}f(0) &= -1{.}5 \sin\left(2\left(0-\frac{3\pi}{4}\right)\right)+1\\ f(0) &= -1{.}5\sin\left(-\frac{6\pi}{4}\right)+1\\ f(0) &= -1{.}5\sin\left(-\frac{3\pi}{2}\right)+1\\ f(0) &=-1{.}5 (1) + 1\\f(0) &= -0{.}5\end{align}||
-
The sign or positive and negative intervals of the function can be found with the zeros. Three consecutive zeros are required: |x_1\approx 2{.}72,| |x_2\approx 3{.}56| and ||\begin{align}x_3 &= x_1+P \\ &= 2{.}72+\pi \\ &\approx 5{.}86\end{align}||
-
The function is positive on the interval |[3{.}56+n \pi,\ 5{.}86+n \pi],| where |n \in \mathbb{Z}.|
-
It is negative on the interval |[2{.}72 + n \pi,\ 3{.}56 + n \pi],| where |n \in \mathbb{Z}.|
-
-
The extrema of the function are:
-
Maximum: |k +{\mid}a{\mid} = 1 + 1{.}5=2{.}5|
-
Minimum: |k - {\mid}a{\mid} = 1 - 1{.}5 = -0{.}5|
-
Both sine and cosine functions are sinusoidal functions. Thus, the same curve can be written with either the cosine or sine function. In this case, the two equations will share the same parameters |\mid a \mid ,| |\mid b \mid| and |k.| Only the parameter |h| will be different. Thus, several properties of the curve can be determined in the same way.
To analyse the parameters and see an example of the properties of a sinusoidal function with the cosine relationship, review the following concept sheet: The Properties of the Cosine Function (Sine).