The study of different trigonometric functions requires a good understanding of the unit circle.
The expression trigonometric function is a general term used to designate the following functions: sine, cosine, tangent, secant, cosecant, and cotangent. The functions represent uniform circular motion. In addition, trigonometric functions are great examples of periodic functions.
The expression inverse trigonometric function is a general term used to designate the following functions: arcsine, arccosine, arctangent, arcsecant, arccosecant, and arccotangent.
Note: For inverse trigonometric functions to be functions, a limit must be placed on their domain and codomain.
Trigonometric functions are periodic functions. A function |f(x)| is periodic if there is a positive number |P| (the period), such as |f(x \pm P)=f(x)| for all values of |x| in the function’s domain.
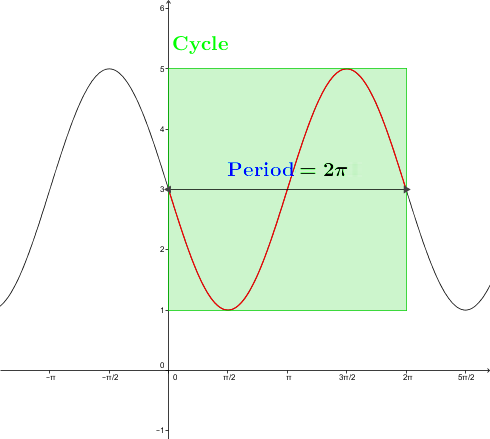
The part of a graph that corresponds to the smallest portion of the curve with a repeating pattern is called the cycle of a trigonometric function.
The distance between two x-coordinates located at the ends of the same cycle is called the period.
A trigonometric function’s frequency the inverse of the period denoted as |\displaystyle F = \frac{1}{P}|, where |P| is the period of the function.
In a given situation, if the x-axis corresponds to time, the frequency corresponds to the number of cycles performed per unit of time.
The following is a graph of a periodic function with a period of |\displaystyle P=\frac{1}{4} \text{second}|. The x-axis corresponds to time in seconds.
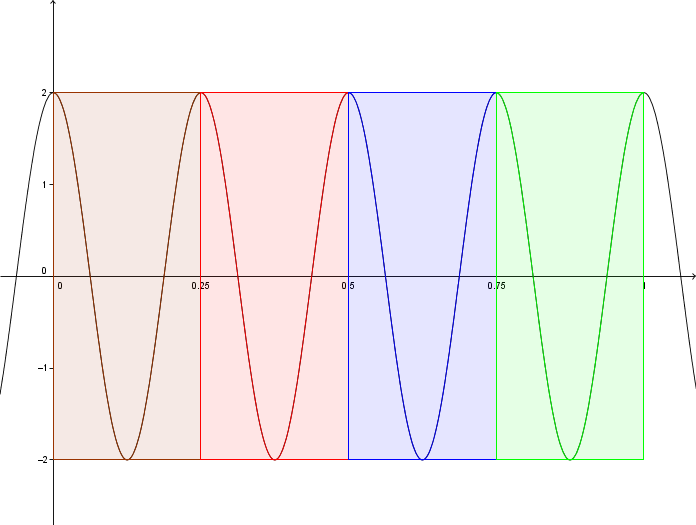
The frequency is |\displaystyle F = \frac{1}{\frac{1}{4}} = 4 \text{ cycles/second}|.
The amplitude of a trigonometric function is half of the value of the difference between the function’s maximum and the minimum.
Note: The definition applies to sine and cosine functions.
The formula for the amplitude of a trigonometric function is: ||A= \frac{\max - \min}{2}.||
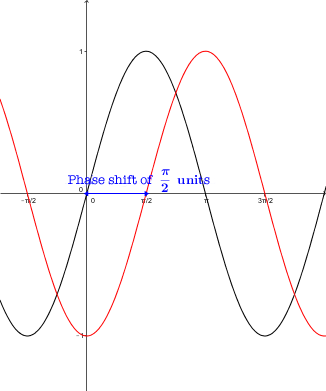
A phase shift is the horizontal translation undergone by the graph of a sine, cosine, or tangent function with respect to the basic function’s graph. The phase shift parameter is denoted by |h|.
The midline of a sine or cosine function corresponds to the horizontal line of equation |y=k| where |k| relates to the vertical translation of the graph with respect to its basic function.

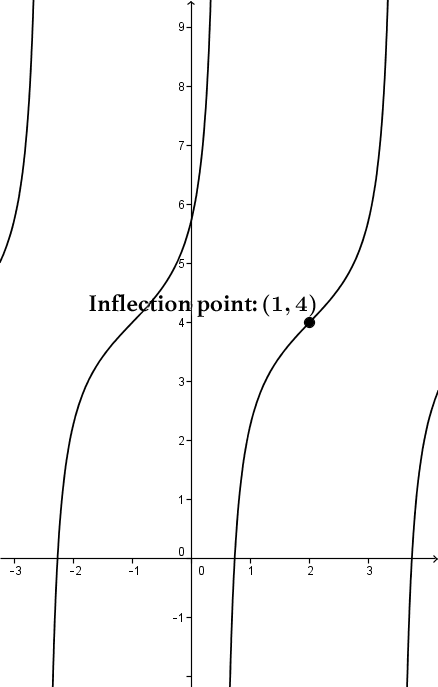
An Inflection point is a point where a curve changes from a convex shape to a non-convex shape. We can also say that an inflection point is a point where a curve changes concavity.
Note:
-
In the sine and tangent functions the inflection point has the coordinates |(h,k)|.
-
The point is not unique.
A sinusoidal function is a function that can be written in the form |f(x)=a \sin(b(x-h))+k|, where |a,b \in \mathbb{R}^*| and |h,k \in \mathbb{R}|.
The sine and cosine functions are sinusoidal functions.