Solving a directly proportional situation comes down to finding a missing term in a proportion. Several methods can be used.
Before solving a directly proportional situation, make sure it is the correct type of situation. It is necessary to know how to recognize a directly proportional situation.
Returning to rate per unit is one way of solving a directly proportional situation. This method is linked to the concept of unit rate.
-
Translate the situation using a proportion where one of the four terms is missing.
-
From the ratio or the rate where the two terms are known, obtain a ratio or an equivalent rate with a denominator of |1.|
-
Calculate the missing term using the ratio or rate.
-
Interpret the results.
Jared earns |$120| for |5| hours of work.
How much will he earn if he works |7| hours?
-
Translate the situation using a proportion where one of the four terms is missing
The situation can result in the following proportion. ||\dfrac{$120}{5\ \text{h}}=\dfrac{?}{7\ \text{h}}|| -
From the ratio or the rate where the two terms are known, obtain a ratio or an equivalent rate with a denominator of |1|
||\dfrac{$120}{5\ \text{h}}\Rightarrow \dfrac{120\color{green}{\div 5}}{5\color{green}{\div 5}}=\dfrac{$24}{1\ \text{h}}|| -
Calculate the missing term using the ratio or rate
Jared earns |$24/\text{h}.|
In |7| hours, he will earn ||7\ \text{h}\times $24/\text{h}=$168|| -
Interpret the results.
In |7| hours, Jared will earn |$168.|
The proportionality ratio present in the proportions can be used to solve a directly proportional situation.
-
Translate the situation using a proportion where one of the four terms is missing.
-
Find the proportionality ratio using the ratio or the rate where the two terms are known.
-
Calculate the missing term using the ratio.
-
Interpret the results.
The following table of values represents the price of salmon in a grocery store as a function of its mass.

How much will a |8.2\ \text{kg}| fillet of salmon cost?
-
Translate the situation using a proportion where one of the four terms is missing
Relying on the two complete points in the table of values, we notice the situation is directly proportional and that the coefficient of proportionality is |\color{red}{3.5}.|

The situation could result in the following proportion.
||\dfrac{7.8\ \text{kg}}{$27.3}=\dfrac{8.2\ \text{kg}}{?}||
-
Find the proportionality ratio using the ratio or rate where the two terms are known
As mentioned above, the proportionality ratio in the situation is |\color{red}{3.5}.| Multiply the mass of the salmon by the proportionality ratio to get the price. -
Calculate the missing term using the coefficient
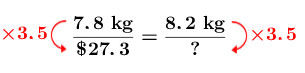
So,
||\begin{align}?&=8.2\times 3.5\\ &=28.7\end{align}||
-
Interpret the results
A fillet of salmon, weighing |8.2\ \text{kg},| costs |$28.70.|
You can also use the factor of change to solve a directly proportional situation.
-
Translate the situation using a proportion where one of the four terms is missing.
-
Determine the factor of change.
-
Calculate the missing term using the factor.
-
Interpret the results.
Mary would like to have her dog's photo enlarged to place it in a frame. The photo is |4| centimetres wide by |9| centimetres high.
What will the height of the enlarged photo be if Mary wants it to be |20\ \text{cm}| wide?
-
Translate the situation using a proportion where one of the four terms is missing
This situation can result in the following proportion. ||\dfrac{\text{width}}{\text{height}}:\dfrac{4\ \text{cm}}{9\ \text{cm}}=\dfrac{20\ \text{cm}}{?}||
Note: If you place the width of the photo in the relation’s numerator, be sure to place the width of the enlarged photo in the same position, i.e., in the numerator of the other relation. -
Determine the factor of change
The factor of change is |\color{red}{5}.|
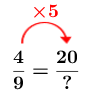
-
Calculate the missing term using the factor
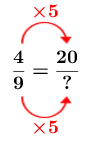
-
Interpret the results
The height of the enlarged photo will be |45\ \text{cm}.|
The famous method of cross multiplication follows directly from the fundamental property of proportions which states that the product of extremes is equal to the product of the means. It is possible to use this method to solve a directly proportional situation. Cross multiplication, or cross product, is often referred to as the Rule of Three or the Fish Method.
-
Translate the situation using a proportion where one of the four terms is missing.
-
Calculate the product of the extremes and the product of the means, then perform the division necessary to determine the value of the missing term.
-
Interpret the results.
Simone plants flowers in her yard. Today, she worked for |4| hours and planted |24| boxes of flowers.
How many boxes of flowers will she plant tomorrow if she only has |3| hours?
-
Translate the situation using a proportion where one of the four terms is missing
This situation can result in the following proportion. ||\dfrac{4\ \text{hours}}{24\ \text{boxes}}=\dfrac{3\ \text{hours}}{?\ \text{boxes}}|| -
Calculate the product of the extremes and the product of the means, then perform the division necessary to determine the value of the missing term
||\begin{align}\dfrac{\color{blue}{4}}{\color{green}{24}}=\dfrac{\color{green}{3}}{\color{blue}{?}} \Rightarrow \color{blue}{4}\times \color{blue}{?}&=\color{green}{24}\times \color{green}{3}\\ \phantom{\dfrac{\color{blue}{4}}{\color{green}{24}}=\dfrac{\color{green}{3}}{\color{blue}{?}}}\color{blue}{4}\times \color{blue}{?}&=\color{green}{72}\\ \phantom{\dfrac{\color{blue}{4}}{\color{green}{24}}=\dfrac{\color{green}{3}}{\color{blue}{?}}} \color{blue}{?}&=\color{green}{72}\div \color{blue}{4}\\\phantom{\dfrac{\color{blue}{4}}{\color{green}{24}}=\dfrac{\color{green}{3}}{\color{blue}{?}}} \color{blue}{?}&=18\end{align}|| -
Interpret the results
Simone will plant |18| boxes of flowers tomorrow.
We see that the method presented in the example above amounts to the same manipulations as the cross multiplication.
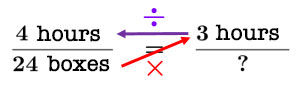
Carrying out the cross multiplication results in the following operations.
||\begin{align}?&=24\color{red}{\times}3\color{purple}{\div}4\\
&=72\color{purple}{\div}4\\
&=18\end{align}|| These are the same operations as those in the previous example.
Before solving a directly proportional situation, ensure that it is the correct type of situation. To do so, it is necessary to know how to recognize an inversely proportional situation.
Inversely proportional situations cannot be resolved like directly proportional situations. The following is one way to resolve them.
In an inversely proportional situation, the product of the associated values of the two variables is constant. The following method is based on this property.
-
Determine the points present in the situation. One of the points will contain a missing value.
-
Calculate the constant product of the situation using the points where you know the two terms, and determine the missing value using the product.
-
Interpret the results.
A school rents a bus for a school trip to Toronto. The cost of the rental will be distributed equally among the students participating in the trip. The school announces that if |15| students participate in the trip, each one will have to pay |$250| for the bus rental.
If |40| students participate in the trip, how much will each one pay?
-
Determine the points present in the situation. One of the points will contain a missing value
The two points are the following. ||\left(15\ \text{students},$250\right)\ \text{and}\ (40\ \text{students},\color{red}{$?})|| -
Calculate the constant product of the situation using the points where two terms are known, and determine the missing value using the product
We know the following. ||\begin{align}15\times 250 &=40\times \color{red}{?}\\ 3750&=40\times \color{red}{?}\\ 3750\div 40&=\ \color{red}{?}\\ 93.75&=\ \color{red}{?}\end{align}|| -
Interpret the results
If |40| students participate in the trip, each one will pay |$93.75| for the bus rental.
Another way to resolve an inversely proportional situation is by reverse cross multiplication (or reverse cross product).
-
Translate the statement into a proportion of ratios where one of the four terms is missing.
-
Reverse the relation that contains the missing term.
-
Perform a cross multiplication.
-
Interpret the results.
A company of industrial painters has just landed a big contract. The boss of the company informs his employees that if |2| painters take on the contract, they will have to work |80| hours to complete it.
How many painters will the boss have to assign to the contract for it to be completed in |16| hours?
-
Translate the statement into a proportion of ratios where one of the four terms is missing
Normally, we would be inclined to translate the situation as follows. ||\dfrac{2\:\text{painters}}{80\:\text{hours}}=\dfrac{\color{red}{?}\:\text{painters}}{16\:\text{hours}}|| Be careful! For this method to work, this situation requires using a proportion of ratios. For the proportion to be a proportion of ratios, we must compare similar quantities on both sides of the equation. The painters to the left of the equation and the respective working times to the right, for example. The following is such a proportion. ||\dfrac{2\:\text{painters}}{\color{red}{?}\:\text{painters}}=\dfrac{80\:\text{hours}}{16\:\text{hours}}|| -
Reverse the ratio that contains the missing term
By inverting the ratio which contains the missing term, the result is the following.

-
Perform a cross multiplication
A cross multiplication can be performed from the new equation. ||\quad\ \begin{align}\dfrac{\color{red}{?}}{2}\ \ =\ \ \dfrac{80}{16}\quad\ \ \Rightarrow \quad\ \ \color{red}{?}&=2\times 80\div 16\\ \\ \color{red}{?}&=10\end{align}|| -
Interpret the results
Therefore, to complete the contract in |16| hours, the boss will have to employ |10| painters.
Pour valider ta compréhension à propos des situations de proportionnalité, des situations inversement proportionnelles et des suites arithmétiques, consulte la MiniRécup suivante.
