La résolution de situations directement ou inversement proportionnelles

Avant de résoudre une situation directement proportionnelle, il faut s'assurer de bien être en présence de ce type de situations. Pour ce faire, il faut savoir reconnaitre une situation directement proportionnelle.

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant.

2. À partir du rapport ou du taux dont on connait les 2 termes, obtenir un rapport ou un taux équivalent dont le dénominateur est 1.

3. Calculer le terme manquant à l'aide de ce rapport ou de ce taux.

4. Interpréter le résultat obtenu.

Sébastien a gagné |120\ $| en |5| heures de travail. Combien gagnera-t-il s'il travaille |7| heures?

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant
   Cette situation peut se traduire par la proportion suivante. ||\dfrac{120\ $}{5\ \text{h}}=\dfrac{?}{7\ \text{h}}||

2. À partir du rapport ou du taux dont on connait les 2 termes, obtenir un rapport ou un taux équivalent dont le dénominateur est 1 ||\dfrac{120\ $}{5\ \text{h}}\Rightarrow \dfrac{120\color{green}{\div 5}}{5\color{green}{\div 5}}=\dfrac{24\ $}{1\ \text{h}}||

3. Calculer le terme manquant à l'aide de ce rapport ou de ce taux
   Sébastien gagne donc |24\ $/\text{h}|. Pour |7| heures, il gagnera |7\ \text{h}\times 24\ $/\text{h}=168\ $|

4. Interpréter le résultat obtenu
   Pour |7| heures, Sébastien gagnera |168\ $.|

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant.

2. Trouver le coefficient de proportionnalité à l'aide du rapport ou du taux dont on connait les 2 termes.

3. Calculer le terme manquant à l'aide de ce coefficient.

4. Interpréter la réponse obtenue.

La table de valeurs suivante représente le prix du saumon dans une épicerie en fonction de sa masse.

Combien coutera une pièce de |8{,}2\ \text{kg}| de saumon?

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant
   En se fiant aux 2 couples complets de la table de valeurs, on remarque qu'il s'agit bien d'une situation directement proportionnelle et que le coefficient de proportionnalité est |\color{#ec0000}{3{,}5}.|

La situation pourrait alors se traduire par la proportion suivante. ||\dfrac{7{,}8\ \text{kg}}{27{,}3\ $}=\dfrac{8{,}2\ \text{kg}}{?}||

2. Trouver le coefficient de proportionnalité à l'aide du rapport ou du taux dont on connait les 2 termes
   Comme il a été mentionné ci-haut, le coefficient de proportionnalité de cette situation est |\color{#ec0000}{3{,}5}|. Il faut multiplier la masse du saumon par ce coefficient pour obtenir le prix.

3. Calculer le terme manquant à l'aide de ce coefficient

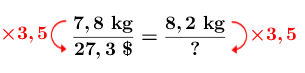
Donc, |?=8{,}2\times 3{,}5=28{,}7.|

4. Interpréter la réponse obtenue
   Une pièce de saumon de |8{,}2\ \text{kg}| coutera |28{,}70\ $.|

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant.

2. Déterminer le facteur de changement.

3. Calculer le terme manquant à l'aide de ce facteur.

4. Interpréter la réponse obtenue.

Marie-Claude souhaite faire agrandir la photo de son chien pour pouvoir la mettre dans un cadre. La photo initiale a |4| centimètres de largeur par |9| centimètres de hauteur.

Quelle sera la hauteur de la photo agrandie si Marie-Claude veut que celle-ci ait une largeur de |20\ \text{cm}|?

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant
   Cette situation peut se traduire par la proportion suivante. ||\dfrac{\text{largeur}}{\text{hauteur}}=\dfrac{4\ \text{cm}}{9\ \text{cm}}=\dfrac{20\ \text{cm}}{?}||**Attention, si on met la largeur de la photo initiale au numérateur du rapport, il faut s'assurer de mettre la largeur de la photo agrandie à la même position, soit au numérateur de l'autre rapport.

2. Déterminer le facteur de changement
   On remarque que le facteur de changement est |\color{#ec0000}{5}.|

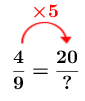
3. Calculer le terme manquant à l'aide de ce facteur.

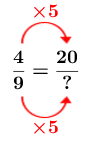
4. Interpréter la réponse
   La hauteur de la photo agrandie sera de |45\ \text{cm}.|

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant.

2. Effectuer le produit des extrêmes et des moyens puis effectuer la division nécessaire pour connaitre la valeur du terme manquant.

3. Interpréter la réponse obtenue.

Simone plante des fleurs sur son terrain. Aujourd'hui, elle a travaillé pendant |4| heures et a réussi à planter les fleurs de |24| boites.

Combien de boites de fleurs réussira-t-elle à planter si, demain, elle n'a que |3| heures à consacrer à cette tâche?

1. Traduire la situation à l'aide d'une proportion dont l'un des 4 termes est manquant
   Cette situation peut se traduire par la proportion suivante. ||\dfrac{4\ \text{heures}}{24\ \text{boites}}=\dfrac{3\ \text{heures}}{?\ \text{boites}}||

2. Effectuer le produit des extrêmes et des moyens puis effectuer la division nécessaire pour connaitre la valeur du terme manquant ||\begin{align} \dfrac{\color{#333fb1}{4}}{\color{#3a9a38}{24}}&=\dfrac{\color{#3a9a38}{3}}{\color{#333fb1}{?}} \\\\ \color{#333fb1}{4}\,\times\,\color{#333fb1}{?}&=\color{#3a9a38}{24}\times \color{#3a9a38}{3}\\ \color{#333fb1}{4}\,\times\,\color{#333fb1}{?}&=72\\ \color{#333fb1}{?}&=72\color{#ec0000}{\div 4}\\ \color{#333fb1}{?}&=\color{#333fb1}{18}\end{align}||

3. Interpréter la réponse obtenue
   Simone pourra planter |18| boites de fleurs demain.

On voit que la méthode présentée dans l'exemple ci-haut revient aux mêmes manipulations que le produit croisé (aussi appelé règle de trois ou méthode du poisson).

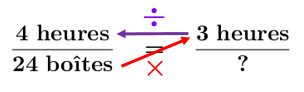
En effet, en effectuant le produit croisé, on obtient les opérations suivantes.||\begin{align}?&=24\boldsymbol{\color{#ec0000}{\times}}3\boldsymbol{\color{#ec0000}{\div}}4\\&=72\boldsymbol{\color{#ec0000}{\div}}4\\&=18\end{align}||Ce sont les mêmes manipulations que celles données dans l'exemple précédent.

Avant de résoudre une situation directement proportionnelle, il faut s'assurer de bien être en présence de ce type de situations. Pour ce faire, il faut savoir reconnaitre une situation inversement proportionnelle.

1. Déterminer les couples présents dans la situation. L'un de ces couples contiendra une valeur manquante.

2. Calculer le produit constant de la situation à l'aide du couple dont on connait les 2 termes et déterminer la valeur manquante à l'aide de ce produit.

3. Interpréter la réponse obtenue.

En vue de faire un voyage scolaire à Toronto, ton école loue un autobus. Le cout de cette location sera distribué équitablement entre les élèves qui participeront au voyage. La direction annonce que si |15| élèves participent au voyage, chacun devra débourser |250\ \$| pour la location de l'autobus.

Si |40| élèves participent au voyage, combien chacun devra-t-il débourser?

1. Déterminer les couples présents dans la situation. L'un de ces couples contiendra une valeur manquante
   Les deux couples sont |\left(15\ \text{élèves},250\ $\right)| et |(40\ \text{élèves},\color{#ec0000}{?}\ $).|

2. Calculer le produit constant de la situation à l'aide du couple dont on connait les 2 termes et déterminer la valeur manquante à l'aide de ce produit ||\begin{align}15\times 250 &=40\,\times\,\color{#ec0000}{?}\\ 3\ 750&=40\,\times\,\color{#ec0000}{?}\\ 3\ 750\div 40&=\ \color{#ec0000}{?}\\ 93{,}75&=\ \color{#ec0000}{?}\end{align}||

3. Interpréter la réponse obtenue
   Si |40| élèves participent au voyage, chacun devra débourser |93{,}75\ $| pour la location de l'autobus.

1. Traduire l'énoncé par une proportion de rapports dont l'un des 4 termes est manquant.

2. Inverser le rapport qui contient le terme manquant.

3. Effectuer un produit croisé.

4. Interpréter la réponse obtenue.

Une compagnie de peintres industriels vient de décrocher un gros contrat. Le patron de la compagnie communique à ses employés que si |2| peintres s'occupent du contrat, chacun devra travailler |80| heures pour le mener à terme.

Combien de peintres le patron devra-t-il mandater pour que le contrat puisse être terminé en |16| heures?

1. Traduire l'énoncé par une proportion de rapports dont l'un des 4 termes est manquant
   Normalement, nous serions porté à traduire cette situation de la façon suivante. ||\dfrac{2\:\text{peintres}}{80\:\text{heures}} =\,\dfrac{\color{#ec0000}{?}\:\text{peintres}}{16\:\text{heures}}||Mais, attention! Pour que cette méthode fonctionne, on doit recourir à une proportion de rapports.
   
   Pour que la proportion soit une proportion de rapports, on doit comparer les grandeurs de même nature de part et d'autre de l'égalité. Les peintres à gauche de l'égalité, et les temps de travail respectifs à droite, par exemple. Voici une telle proportion. ||\dfrac{2\:\text{peintres}}{\color{#ec0000}{?}\:\text{peintres}}=\dfrac{80\:\text{heures}}{16\:\text{heures}}||

2. Inverser le rapport qui contient le terme manquant.
   En inversant le rapport qui contient le terme manquant, on obtient ceci.

3. Effectuer un produit croisé
   À partir de cette nouvelle égalité, on effectue un produit croisé. ||\begin{align}\dfrac{\color{#ec0000}{?}}{2} &= \dfrac{80}{16}\\\\ \Rightarrow \quad\ \color{#ec0000}{?}\,&=2\times 80\div 16\\&=10\end{align}||

4. Interpréter la réponse obtenue
   Pour terminer le contrat en |16| heures, le patron devra donc mandater |10| peintres.