Adding the parameters |a,| |b,| |h,| and |k| to the basic form |f(x)= \log_c x| results in what is called the standard form (also called the transformed form) of the logarithmic function.
The transformed logarithmic function is usually written like so: ||f(x)=a \log_c (b(x-h)) +k|| where |a,b,h,| and |k| act as parameters.
Note : The parameters |a| and |b| are always non-zero.
The base of the function |(c)| must be greater than |0| and not |1.|
In the following interactive animation, experiment with the values of parameters |a|, |b|, |c|, |h,| and |k| of the logarithmic function. Observe the modifications which take place on the transformed curve (in black) compared to the base function with |c=2| (in green). Observe the effect of modifying the parameters on the function’s properties.
When |a>1|
The graph stretches vertically compared to the base function. The greater the absolute value of the parameter |a|, the farther away the curve of the log function is from the |x|-axis.
When |0< a <1|
The graph contracts vertically relative to the base function. The smaller the absolute value of the parameter |a| (closer to |0|), the closer the curve of the log function is to the |x|-axis.

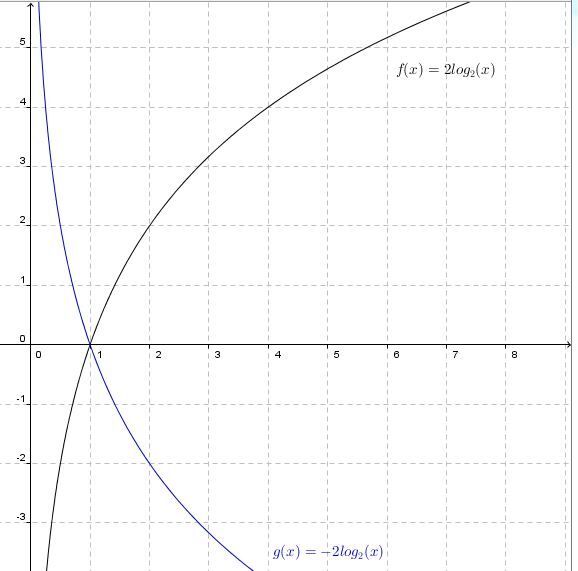
When |a| is positive |a>0|
The curve of the logarithmic function is increasing.
When |a| is negative |a<0|
The curve of the logarithmic function is decreasing.
When |b>1|
The graph contracts horizontally relative to the base function. The larger the absolute value of the parameter |b|, the more the curve of the logarithm function approaches the |y|-axis.
When |0<b<1|
The graph stretches horizontally relative to the base function. The smaller (close to |0|) the absolute value of the parameter |b|, the farther the curve of the logarithm function is from the |y|-axis.
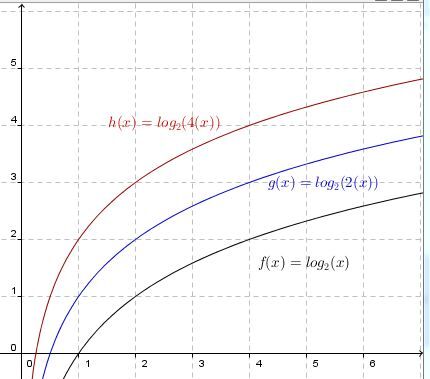
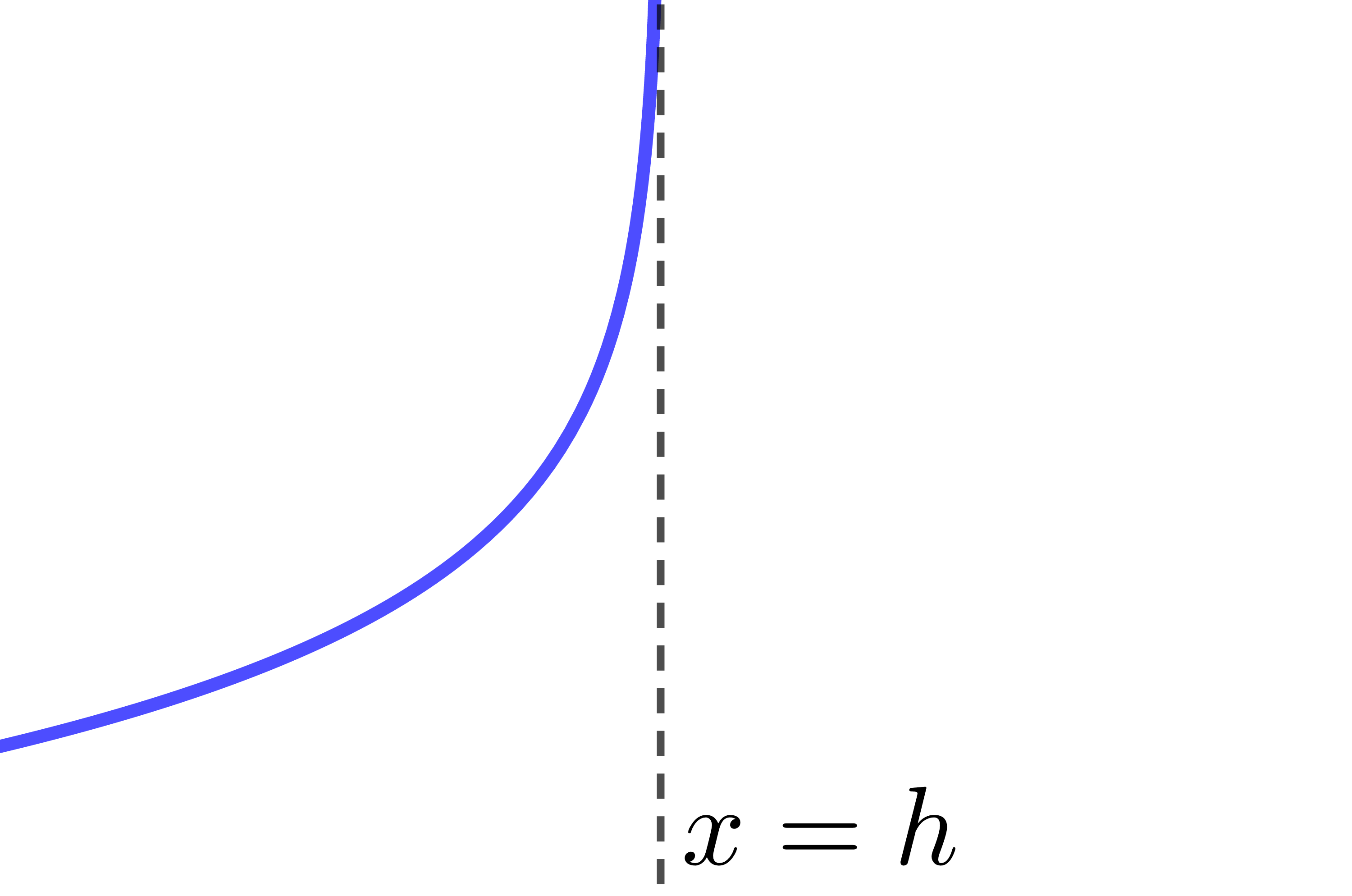
When |b| is positive |b>0|
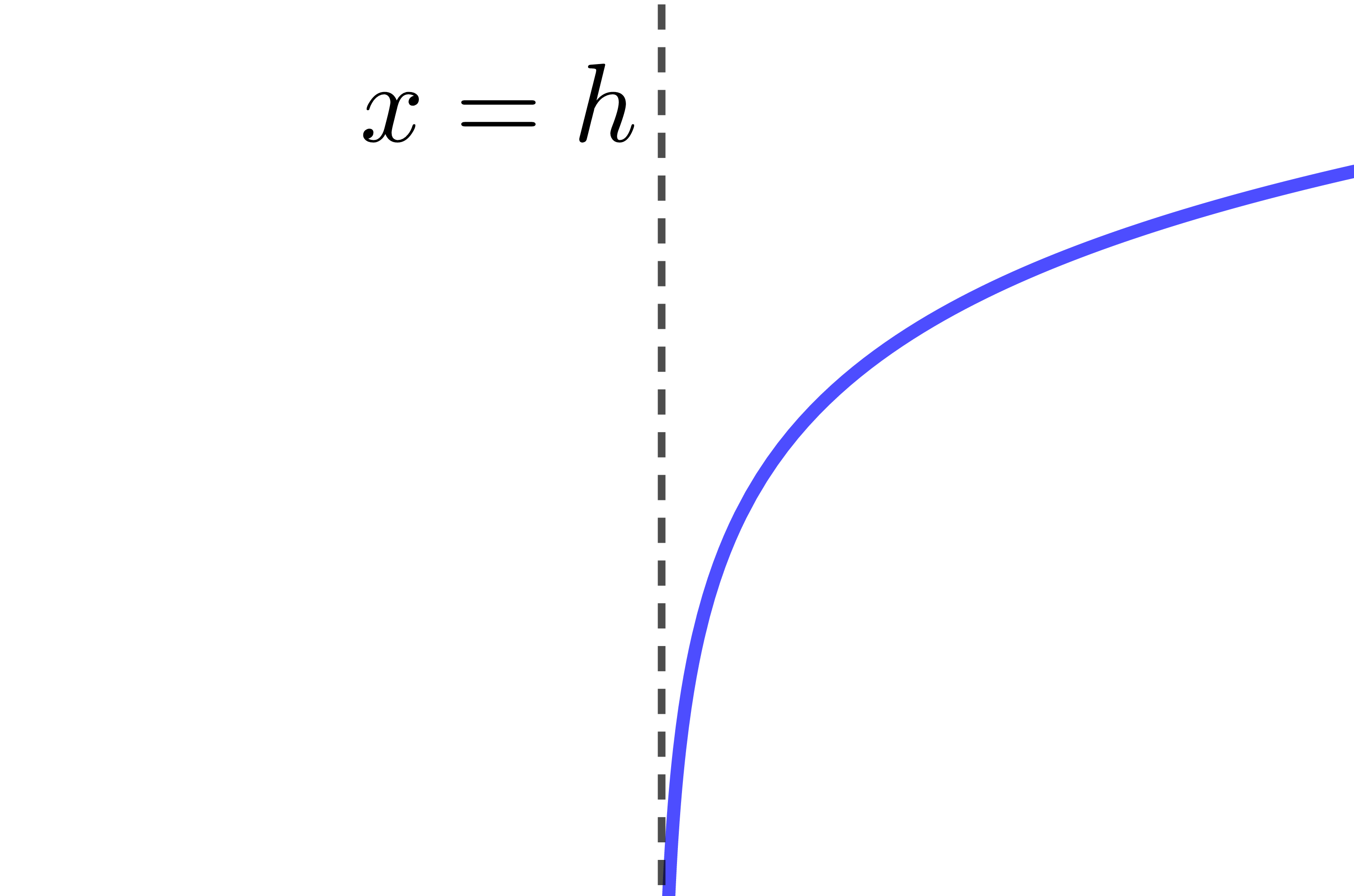
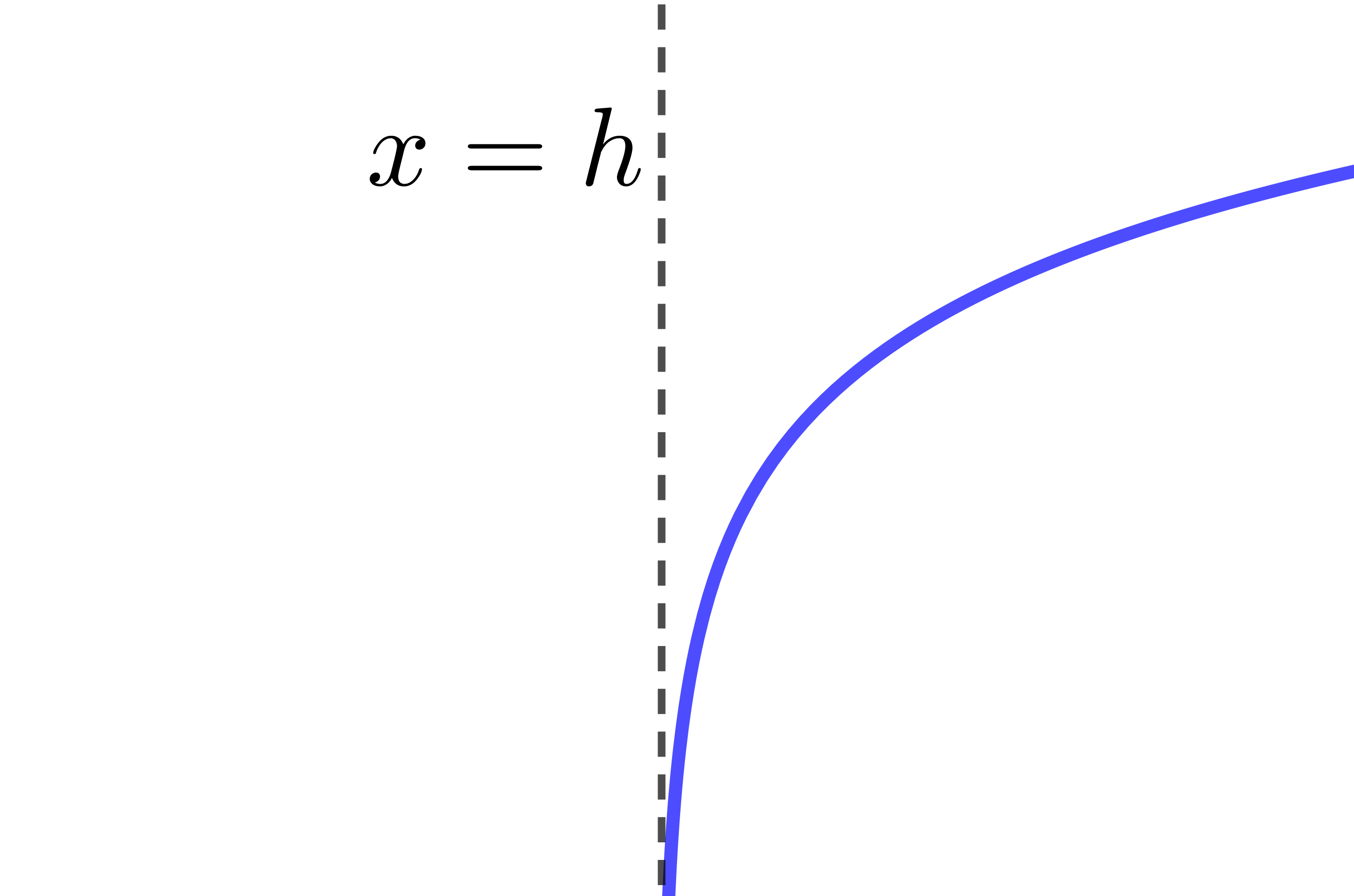
The curve of the logarithmic function is entirely located to the right of the asymptote.
When |b| is negative |b<0|
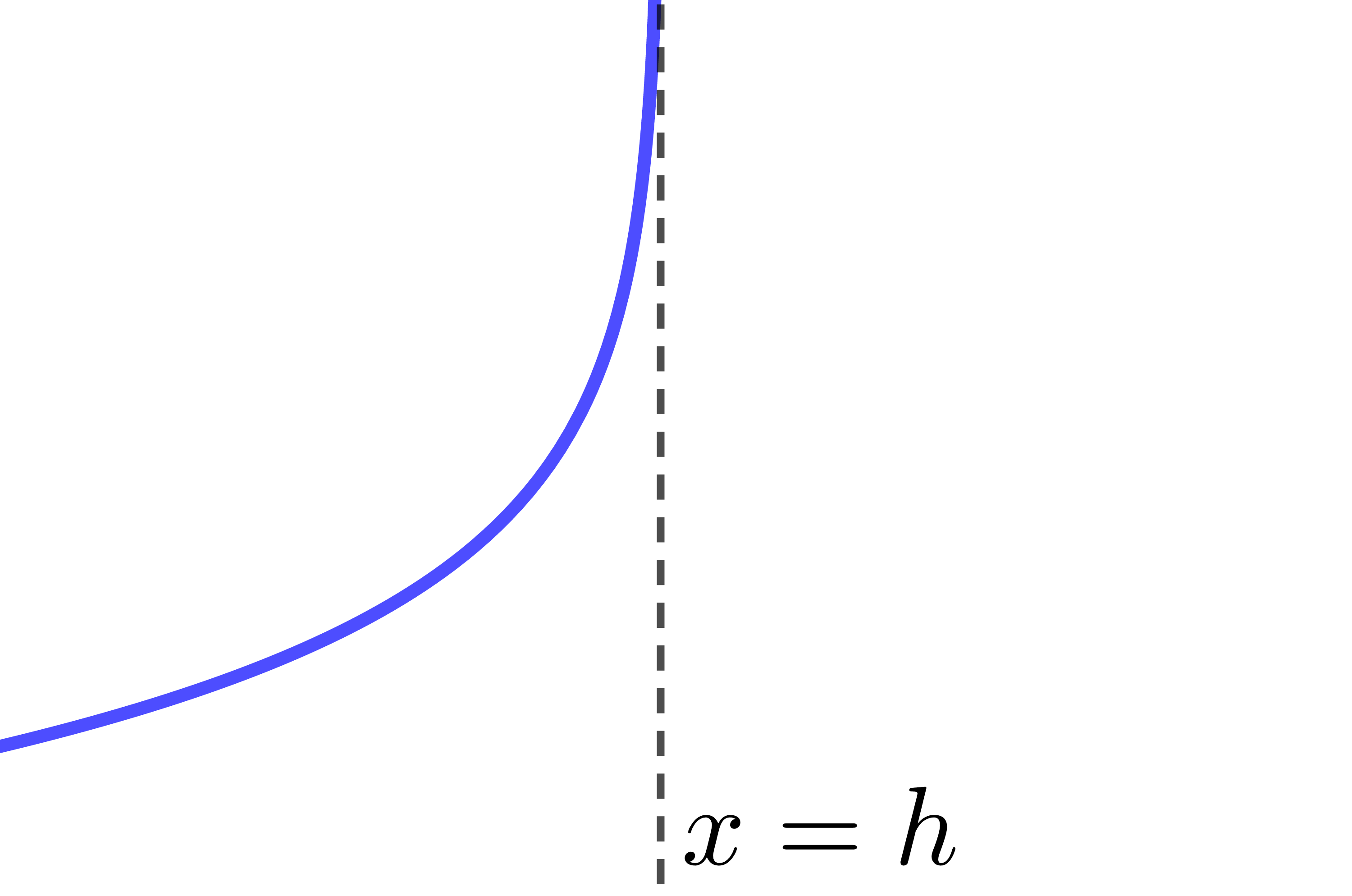
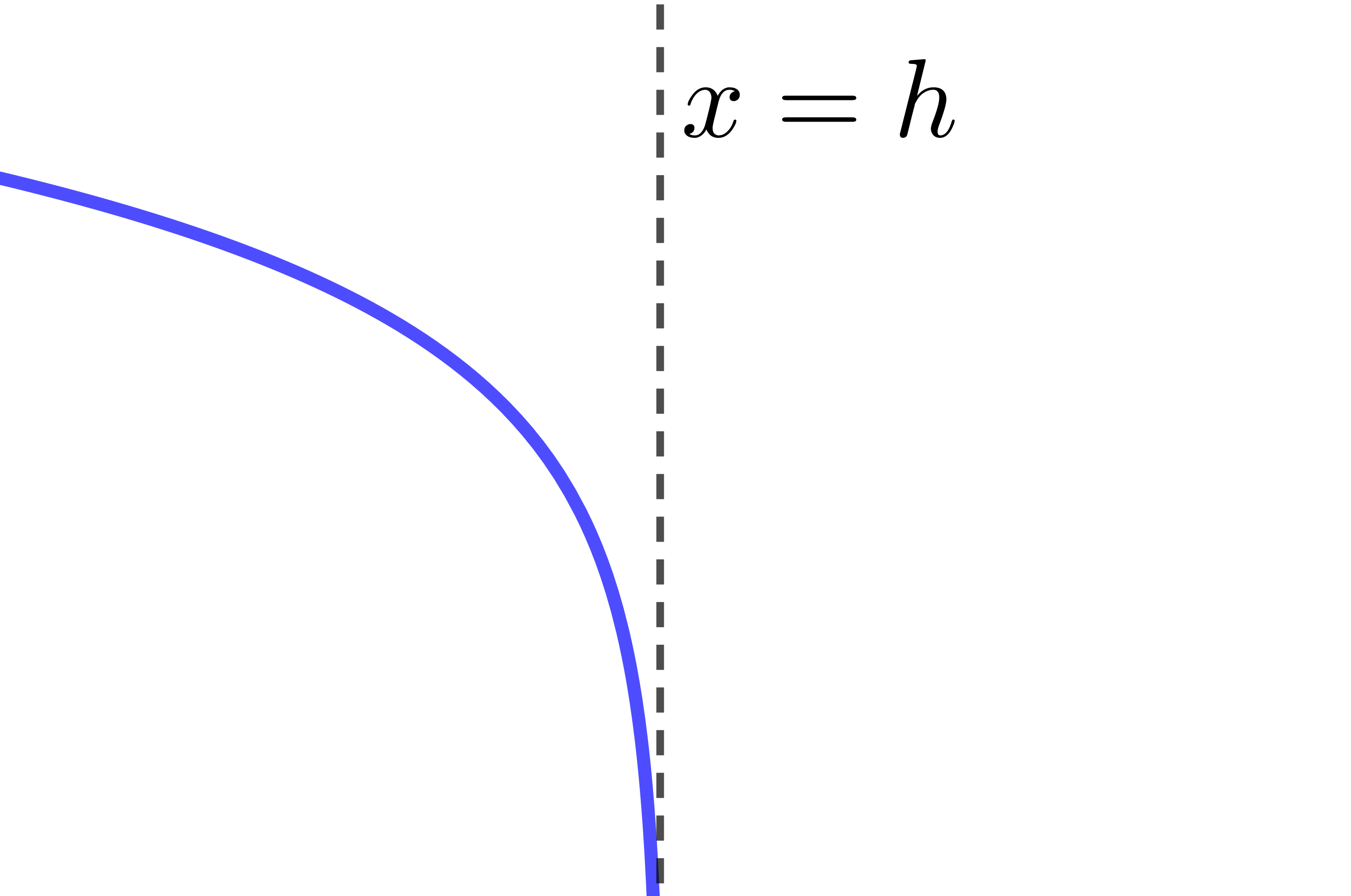
The curve of the logarithmic function is entirely located to the left of the asymptote.
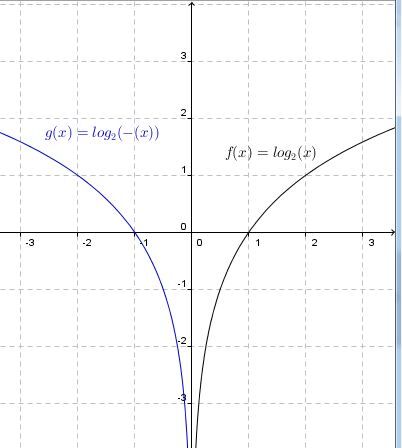
The value of |c| represents the base of the function, that is the multiplying factor present in the exponential function.
When |c>1|
The basic function is increasing.
When |0<c<1|
The basic function is decreasing.
Note that |\log_c x = -\log_{\frac{1}{c}} x|.
Using this property, it is possible to transform a logarithm with a base between |0| and |1| into a logarithm with a base greater than |1|.
According to the property |\log_c x = -\log_{\frac{1}{c}} x,| the function |f(x)=-\log_{\frac{1}{2}}x| is equivalent to the function whose equation is |f(x)=\log_2 x.|
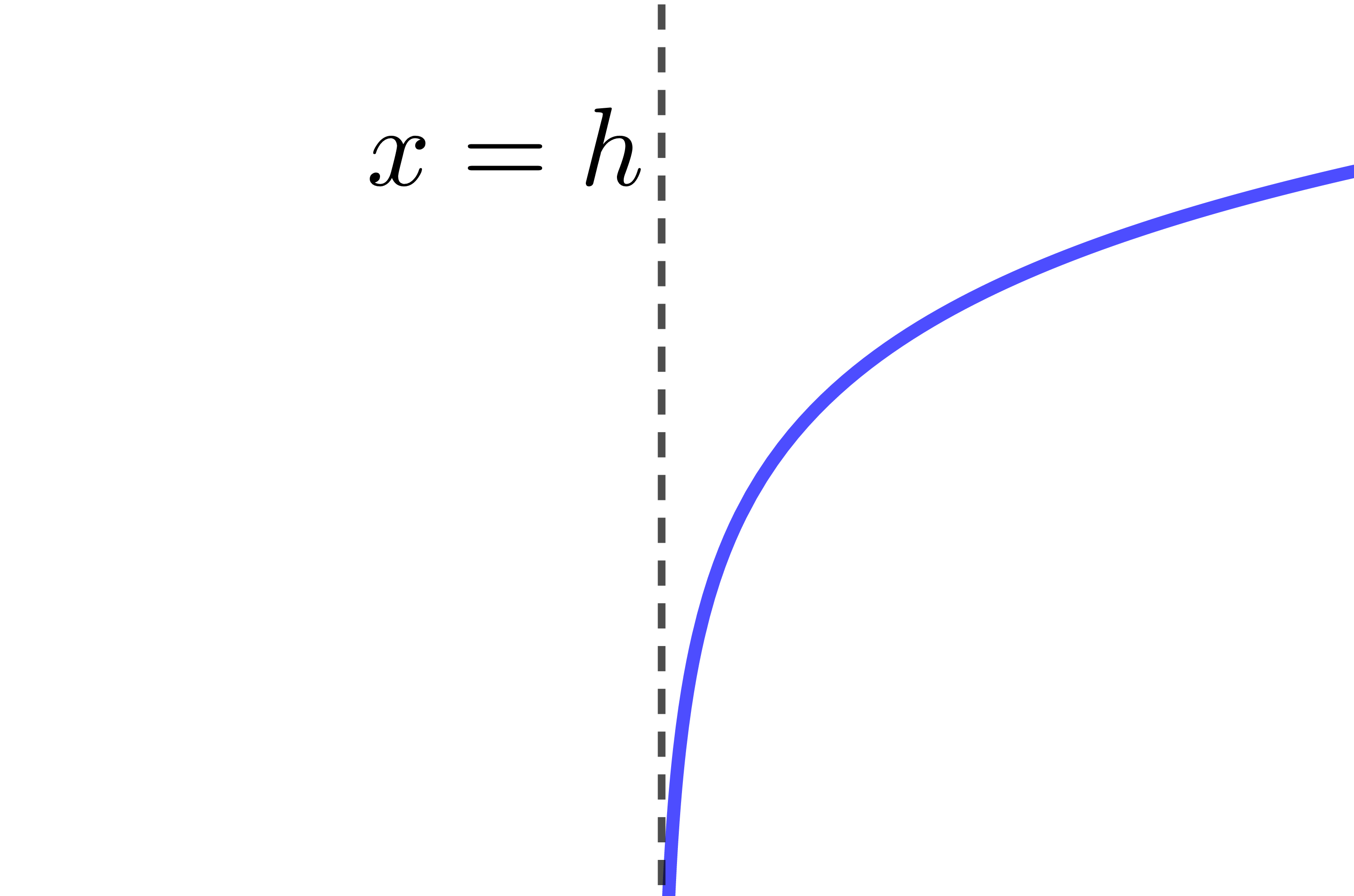
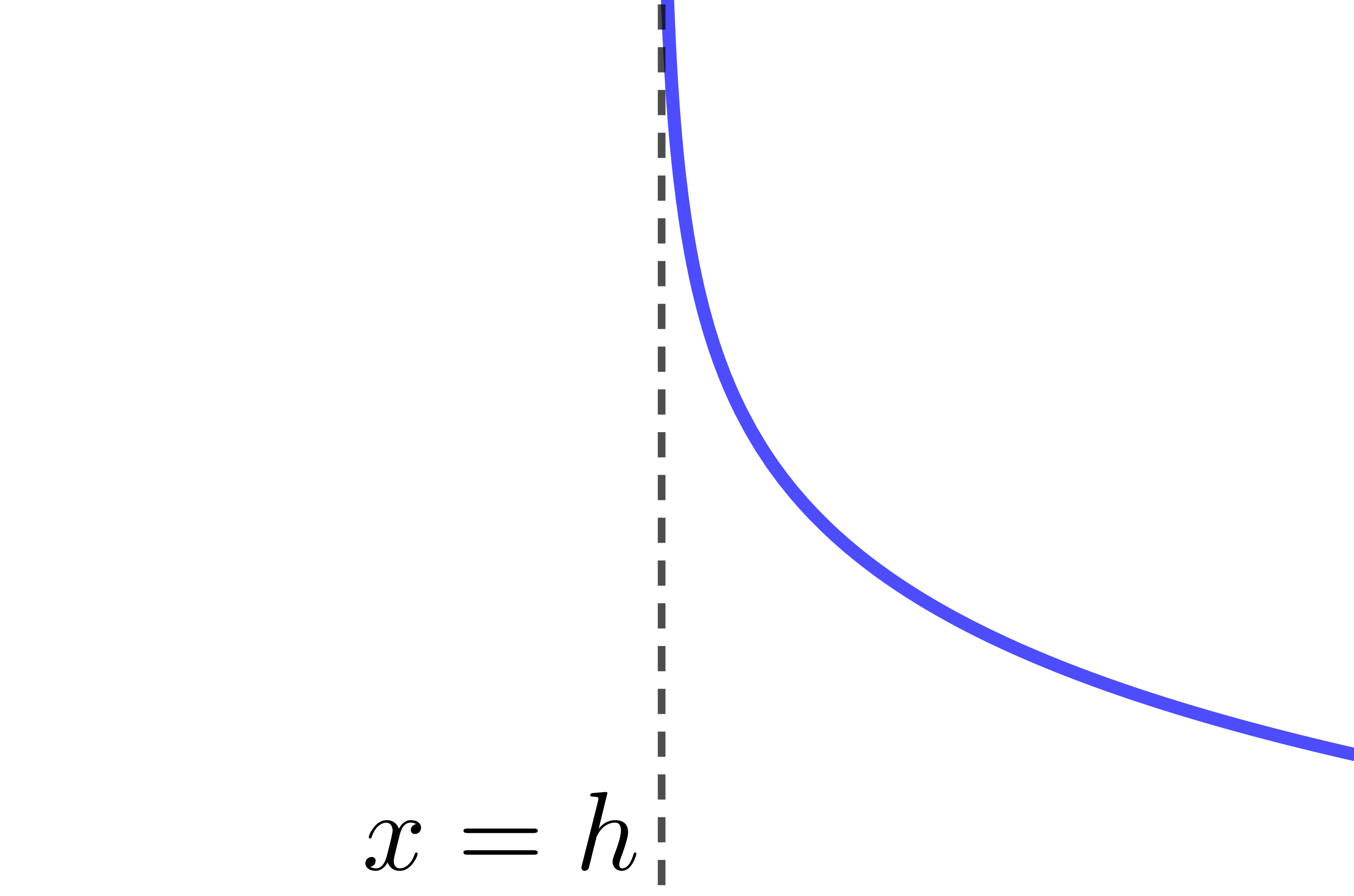
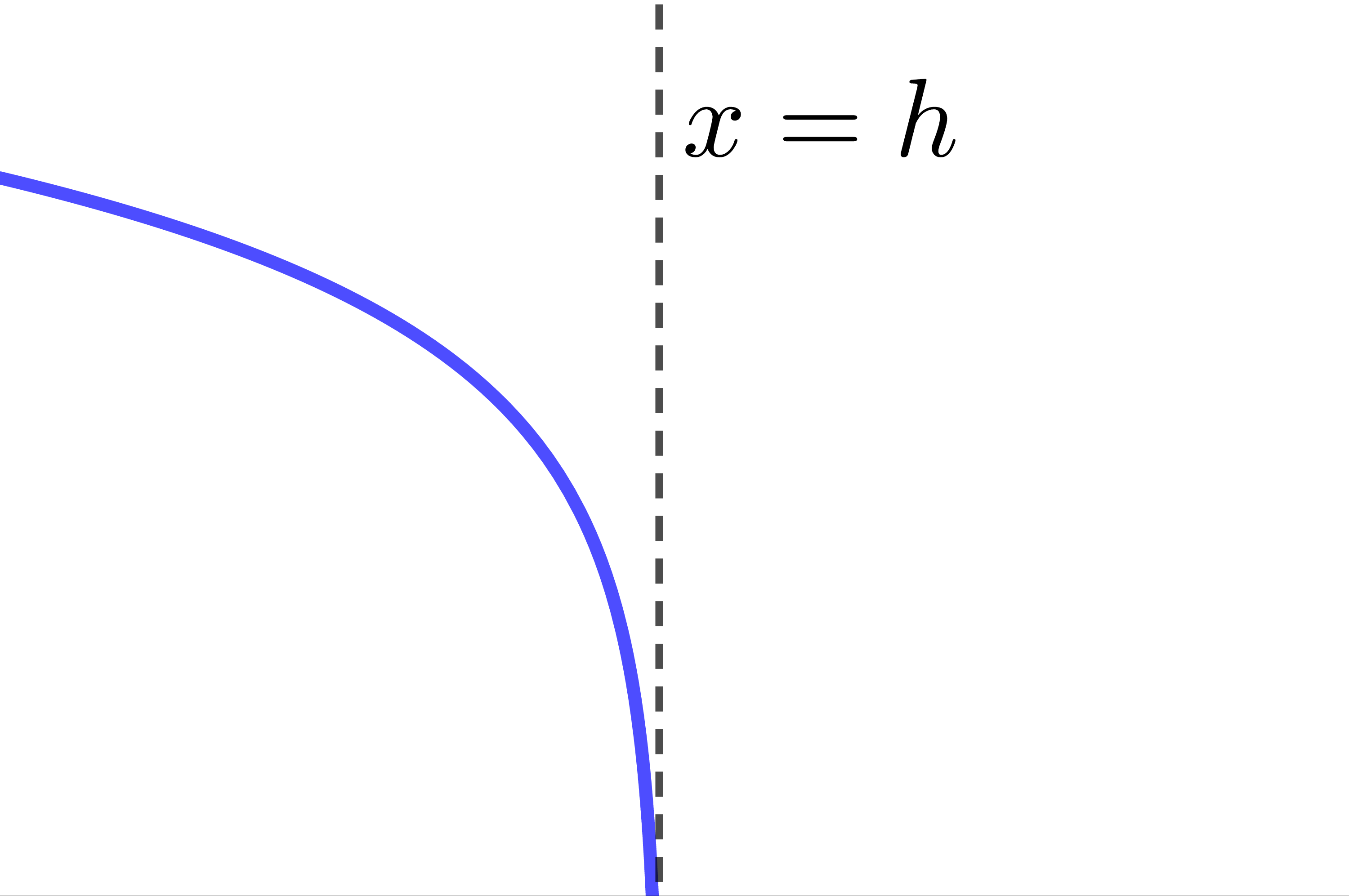
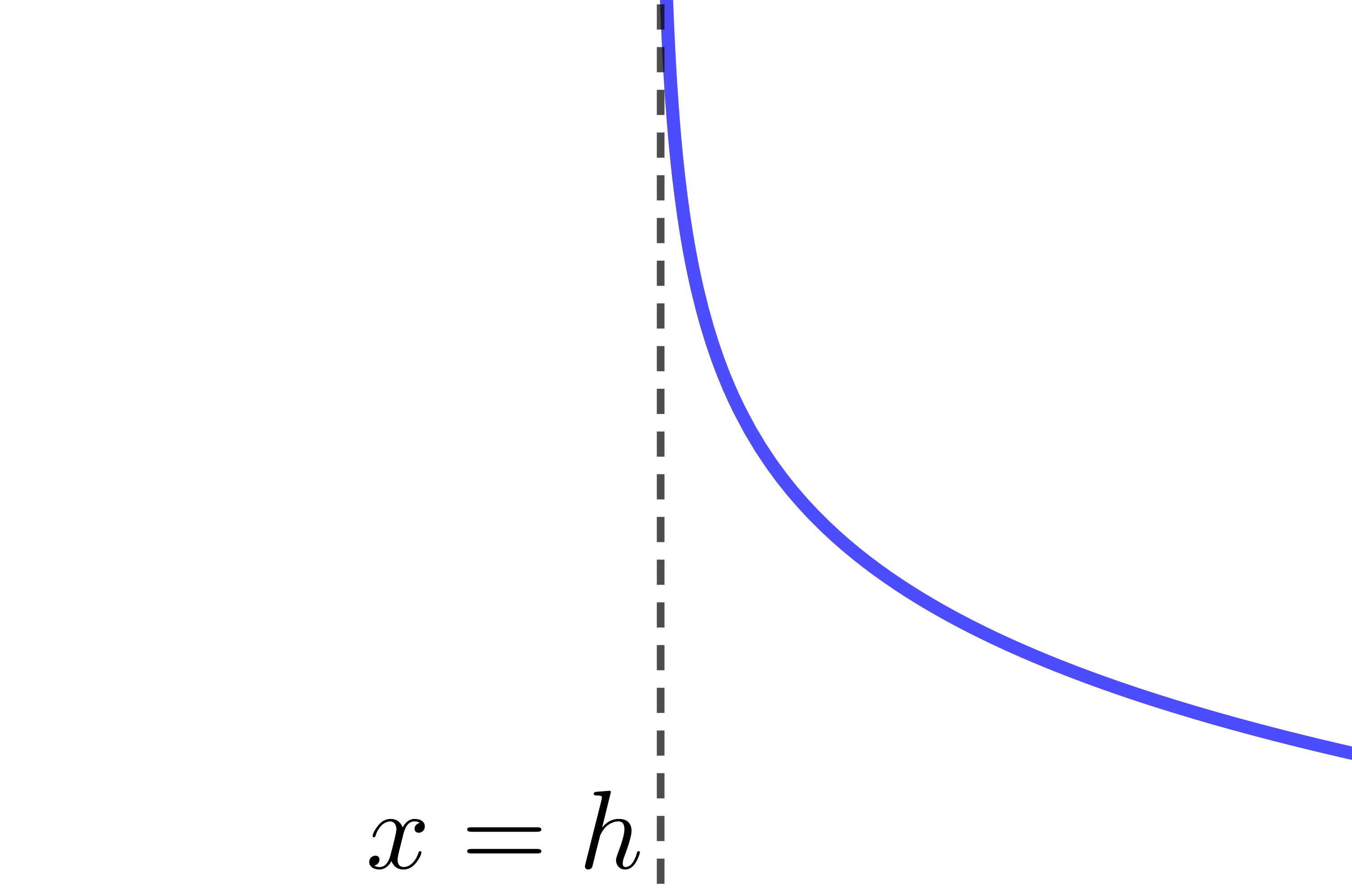
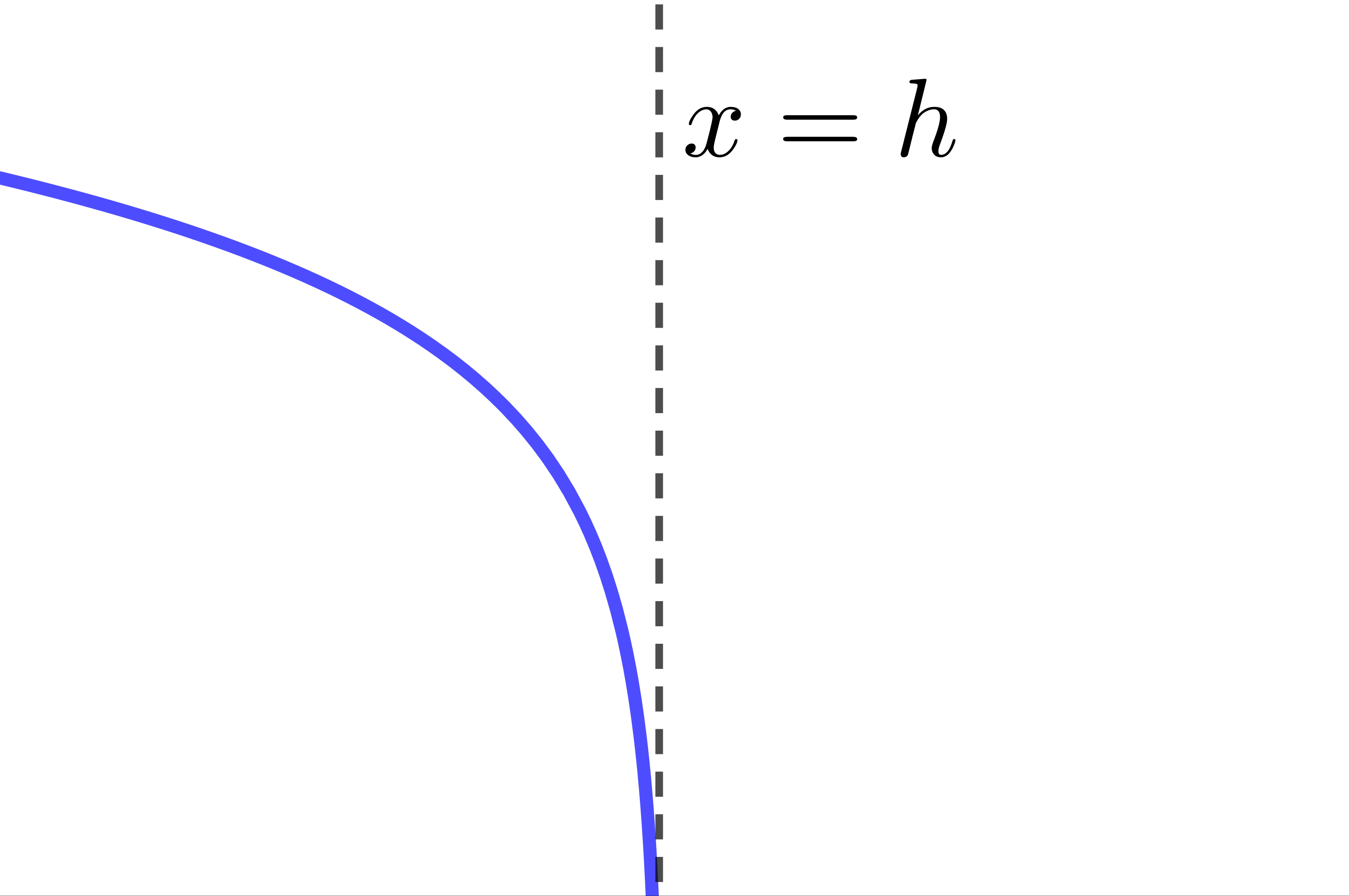
When |h| is positive |h>0|
The curve of the logarithmic function moves to the right.
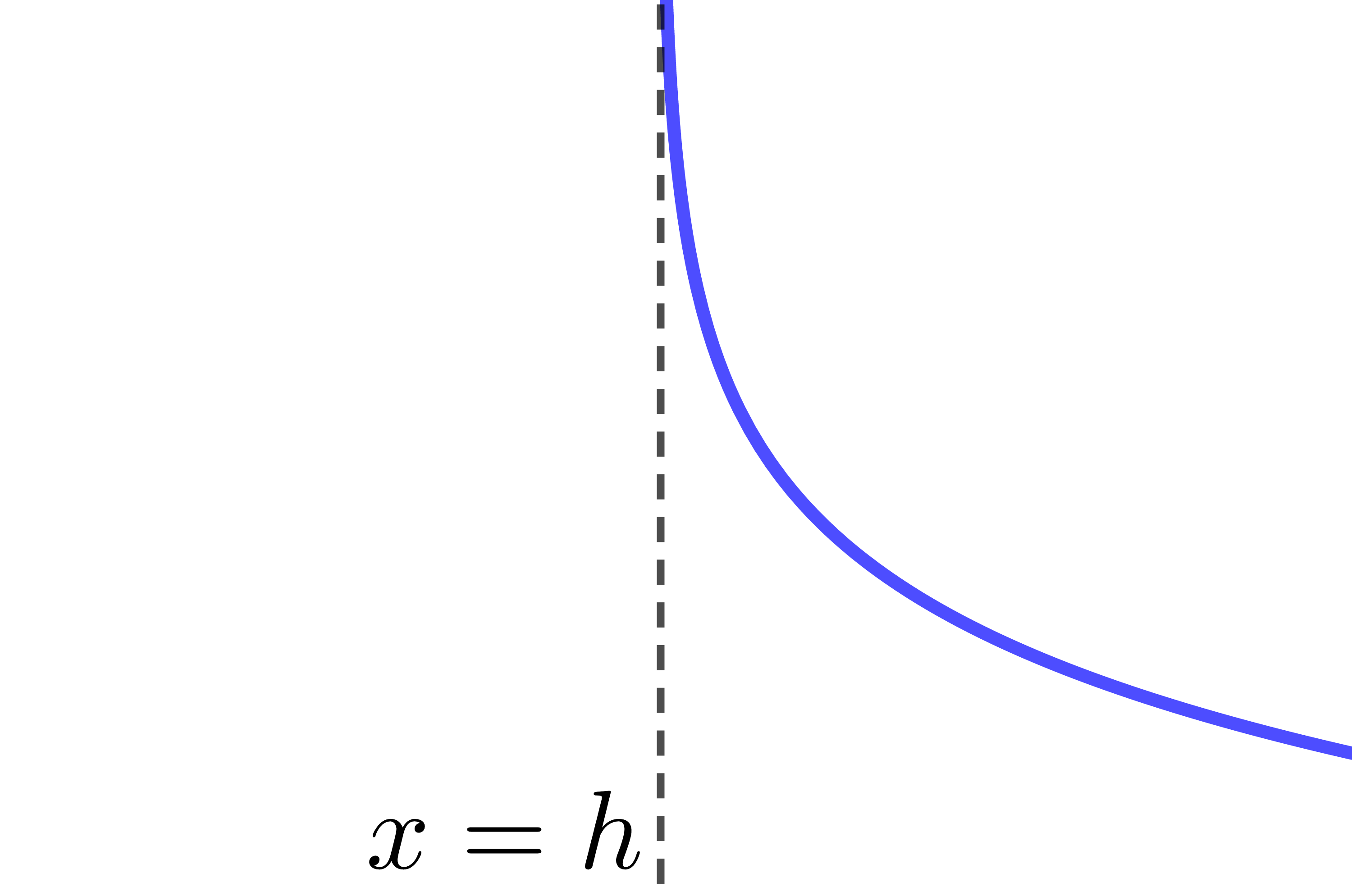
When |h| is negative |h<0|
The curve of the logarithmic function moves to the left.
The asymptote of the logarithmic function has the equation |x=h.| Therefore, if the value of the parameter |h| changes, the location of the asymptote also changes.
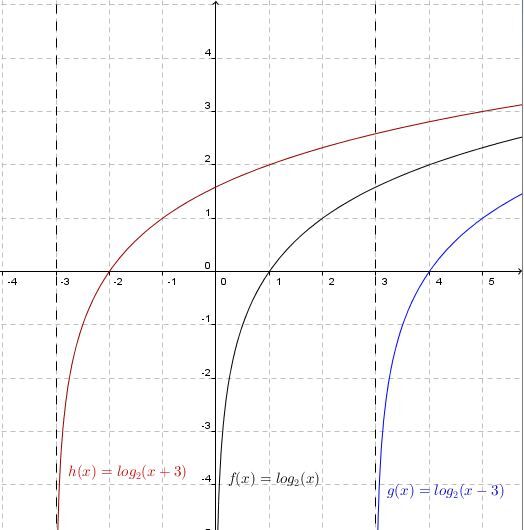
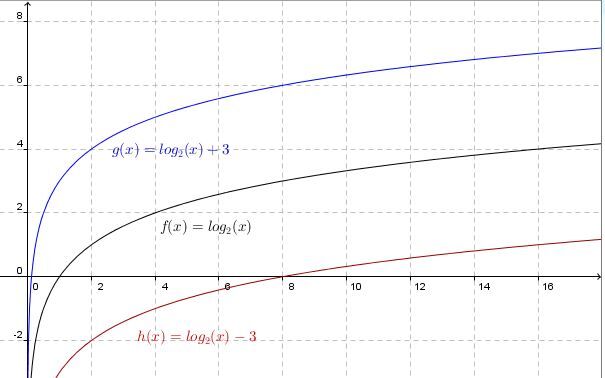
When |k| is positive |k>0|
The curve of the logarithmic function moves upwards.
When |k| is negative |k<0|
The curve of the logarithmic function moves downward.
If |c>1|
|
|
|a>0| |
|a<0| |
|---|---|---|
|
|b>0| |
|
|
|
|b<0| |
|
|
If |0<c<1|
|
|
|a>0| |
|a<0| |
|---|---|---|
|
|b>0| |
|
|
|
|b<0| |
|
|
As seen in the summary table above, certain combinations of parameters give the same result. For example, having |c>1,| |a>0,| and |b>0| is equivalent to having |0<c<1,| |a<0| et |b>0.|
|
|
|b>0| |
|b<0| |
|---|---|---|
|
|c>1| |
|
|
|
|0<c<1| |
|
|