For most functions, there are several equations that can be used to express the same curve. It is very practical to use a form that gives as much information as possible, and the standard form is one such form.
The standard form is a parametric form of writing the equation of a function. The standard form of a function is important since it gives information about the shape of the graph. It is also called transformed form.
The equation of a function written in standard form has parameters.
A parameter is a quantity with a fixed numerical value in an algebraic expression or an equation. The different parameters are generally denoted by letters (which are different from the variables).
By experimenting with the parameters, it is possible to obtain a curve with a different appearance from the basic shape. The curve can be translated, elongated, narrowed, or reflected.
There are generally |4| parameters, denoted |a|, |b|, |h|, and |k|. These parameters all have distinct roles. The |4| parameters can be grouped into |2| categories: additive parameters and multiplicative parameters.
The equation of the basic function |y=f(x)| can be converted to its standard form by adding parameters.
||y=af\big(b(x-h)\big)+k|| where |f| is the function.
The formula above shows the location of the various parameters after they are added to the basic equation.
Here is a table that shows the basic form, standard form, and simplified standard form of various functions.
|
Basic form |
Standard form |
Simplified standard form |
|---|---|---|
|
|y=x| |
|y=a\big(b(x-h)\big)+k| |
|y=ax+k| |
|
|y=x^2| |
|y=a\big(b(x-h)\big)^2+k| |
|y=a(x-h)^2+k| |
|
|y=\dfrac{1}{x}| |
|y=\dfrac{a}{b(x-h)}+k| |
|y=\dfrac{a}{x-h}+k| |
|
|y=[x]| |
|y=a[b(x-h)]+k| |
|
|
|y=\vert x\vert| |
|y=a\vert b(x-h) \vert +k| |
|y=a\vert x-h \vert +k| |
|
|y=\sqrt{x}| |
|y=a \sqrt{b(x-h)}+k| |
|y=a \sqrt{\pm(x-h)}+k| |
|
|y=c^x| |
|y=a(c)^{b(x-h)}+k| |
|y=a(c)^{x}+k| |
|
|y=\log_c (x)| |
|y=a\log_c \big(b(x-h)\big) +k| |
|y=\log_c \big(b(x-h)\big)| or |y=\log_c \big(\pm(x-h)\big) +k| |
|
|y=\sin (x)| |
|y=a \sin \big(b(x-h)\big)+k| |
|
|
|y=\cos (x)| |
|y=a \cos \big(b(x-h)\big)+k| |
|
|
|y=\tan (x)| |
|y=a \tan \big(b(x-h)\big)+k| |
In the following animation, select a function and experiment with its parameters |a|, |b|, |h|, and |k|, as well as the base |c| for exponential and logarithmic functions. Observe the changes that take place on the transformed curve compared to the base function. Afterwards, keep reading the concept sheet to learn more about the additive (|h| and |k|) and multiplicative (|a| and |b|) parameters.
The additive parameters shift a function horizontally or vertically, without changing the function’s appearance. Generally these movements are referred to as translations or shifts.
The parameter |h| has the effect of horizontally shifting a function to the left or right, depending on its value.
-
|h<0:| Translation to the left
-
|h>0:| Translation to the right
To find the value of the parameter |h,| the function must be written in standard form: |y=af\big(b(x-h)\big)+k.| In this form, the parameter |h| is the number to the right of the minus sign in the bracket.
-
In |f(x)=(x \color{red}{-} \color{green}{5})^2+1|, |h| is |\color{green}{5}| and not |-5|.
-
In |g(x)=3(x+8)^2|, it is possible to rewrite the function, as follows: |g(x)=3(x\color{red}{-}\color{green}{\text{-}8})^2|. The result is that |h| is |\color{green}{\text{-}8}| and not |8|.
-
In |h(x)=(2x-12)^2|, it is logical to think that |h=12|, but the function is not in standard form, which can be confusing. Put the function in standard form like so: ||\begin{align} h(x) &=(2x-12)^2 \\ &= \big(2(x-6)\big)^2 \\ &= 2^2(x-6)^2 \\ &= 4(x \color{red}{-} \color{green}{6})^2 \end{align}|| |h| is therefore |\color{green}{6}|.
In this example, the basic form of the absolute value function has the equation |f(x)=\mid x \mid.| After adding the parameter |h,| the equation becomes |f(x)=\mid x-h \mid.|
The parameter |k| has the effect of shifting a function downwards or upwards, depending on its value.
-
|k<0|: Downward translation
-
|k>0|: Upward translation
In this example, the basic equation of the absolute value function is |f(x)=\mid x \mid.| After adding the parameter |k,| the equation becomes |f(x)= \mid x \mid + k.|
The multiplicative parameters change how the function stretches and sometimes induce reflections.
A change of scale, or scaling, in a Cartesian plane is a transformation which modifies the appearance of the graph.
A function can undergo a vertical scaling by |a| or a horizontal scaling by |\dfrac{1}{b}|.
When the function is stretched horizontally |\leftarrow \cdot \rightarrow| or vertically ↑⋅↓↑⋅↓1b1ba1ba1b1b1b1b1ba1b1b1b1b1b1b1b1b1b1b1b1bb, the words elongation or stretching can be used.
When the function is compressed horizontally |\rightarrow \cdot \leftarrow| or vertically ↓⋅↑↓⋅↑aaxaxaaaaaxaaaaaaa→⋅←→⋅←→⋅←→⋅←→⋅←1b,the words shrinking or contraction can be used.
The parameter |a| can make a function undergo a vertical scaling by stretching or contracting it, depending on its value. As well, if the parameter |a| is negative, it causes a reflection relative to the |x|-axis of the function. The vertical scaling is always by a factor of |a,| meaning the |y|-coordinates of the points are multiplied by |a|.
-
|\mid a \mid > 1|: Vertical elongation or stretching
-
|0 < \mid a \mid < 1|: Vertical contraction or shrinking
-
|a < 0|: Reflection relative to the |x|-axis
In this example, the basic form of the square root function equation is |f(x)=\sqrt{x}.| After adding the parameter |a|, the equation becomes |f(x)=a\sqrt{x}.|
The parameter |b| can make a function to undergo a horizontal scaling by stretching or contracting it, depending on its value. As well, if the parameter |b| is negative, it causes a reflection across the |y|-axis of the function. The function is always scaled by a factor of |\dfrac{1}{b},| that is, that the |x|-coordinates of the points are multiplied by the latter.
-
|0 < \mid b \mid < 1|: Horizontal elongation or stretching
-
|\mid\ b \mid > 1|: Horizontal contraction or shrinking
-
|b < 0|: Reflection across the |y|-axis
In this example, the basic form of the equation for a square root function is |f(x)=\sqrt{x}|. After adding the parameter |b|, the equation becomes |f(x)=\sqrt{bx}.|
The transformation that connects a point of a function in standard form to a point of a function is basic form is: ||(x,y) \mapsto \left(\dfrac{x}{b}+h, ay+k \right)||
So, take a point |(x,y)| from the original function, apply the parameters of the standard form, and the new point will be: |\left(\dfrac{x}{b}+h, ay+k \right).|
Consider the basic quadratic function with the equation |y=x^2|.
Transform the equation to obtain the standard form. ||y=-3(x+1)^2+12||
Here, |b=1.|
Consider the following table of values and graph.
|
|x| |
|-3| |
|-2| |
|-1| |
|0| |
|1| |
|2| |
|3| |
|---|---|---|---|---|---|---|---|
|
|y| |
|9| |
|4| |
|1| |
|0| |
|1| |
|4| |
|9| |
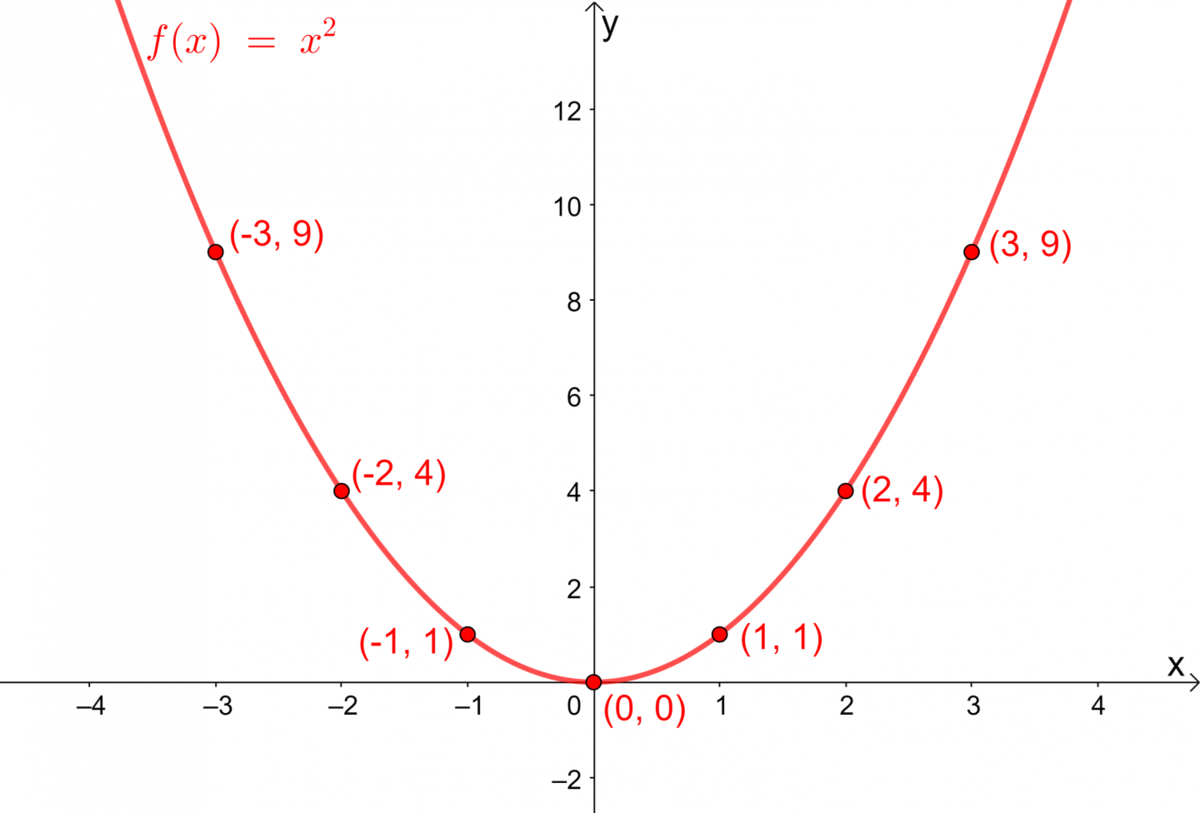
Now apply the transformations given by the parameters using the following transformation: |(x,y) \mapsto \left(\dfrac{x}{b}+h, ay+k \right)|
Calculate the coordinates of the new points |(x', y')| in the following table.
|
Basic coordinates |
Transformed coordinates |
|---|---|
|
|(x,y)| |
|\left(\dfrac{x}{1}-1,-3y+12\right)| |=(x', y')| |
|
|(-3,9)| |
|\left(\dfrac{-3}{1}-1,-3(9)+12\right)| |=(-4,-15)| |
|
|(-2,4)| |
|\left(\dfrac{-2}{1}-1,-3(4)+12\right)| |=(-3,0)| |
|
|(-1,1)| |
|\left(\dfrac{-1}{1}-1,-3(1)+12\right)| |=(-2,9)| |
|
|(0,0)| |
|\left(\dfrac{0}{1}-1,-3(0)+12\right)| |=(-1,12)| |
|
|(1,1)| |
|\left(\dfrac{1}{1}-1,-3(1)+12\right)| |=(0, 9)| |
|
|(2,4)| |
|\left(\dfrac{2}{1}-1,-3(4)+12\right)| |=(1, 0)| |
|
|(3,9)| |
|\left(\dfrac{3}{1}-1,-3(9)+12\right)| |=(2,-15)| |
The two curves can now be plotted in the graph opposite to each other.
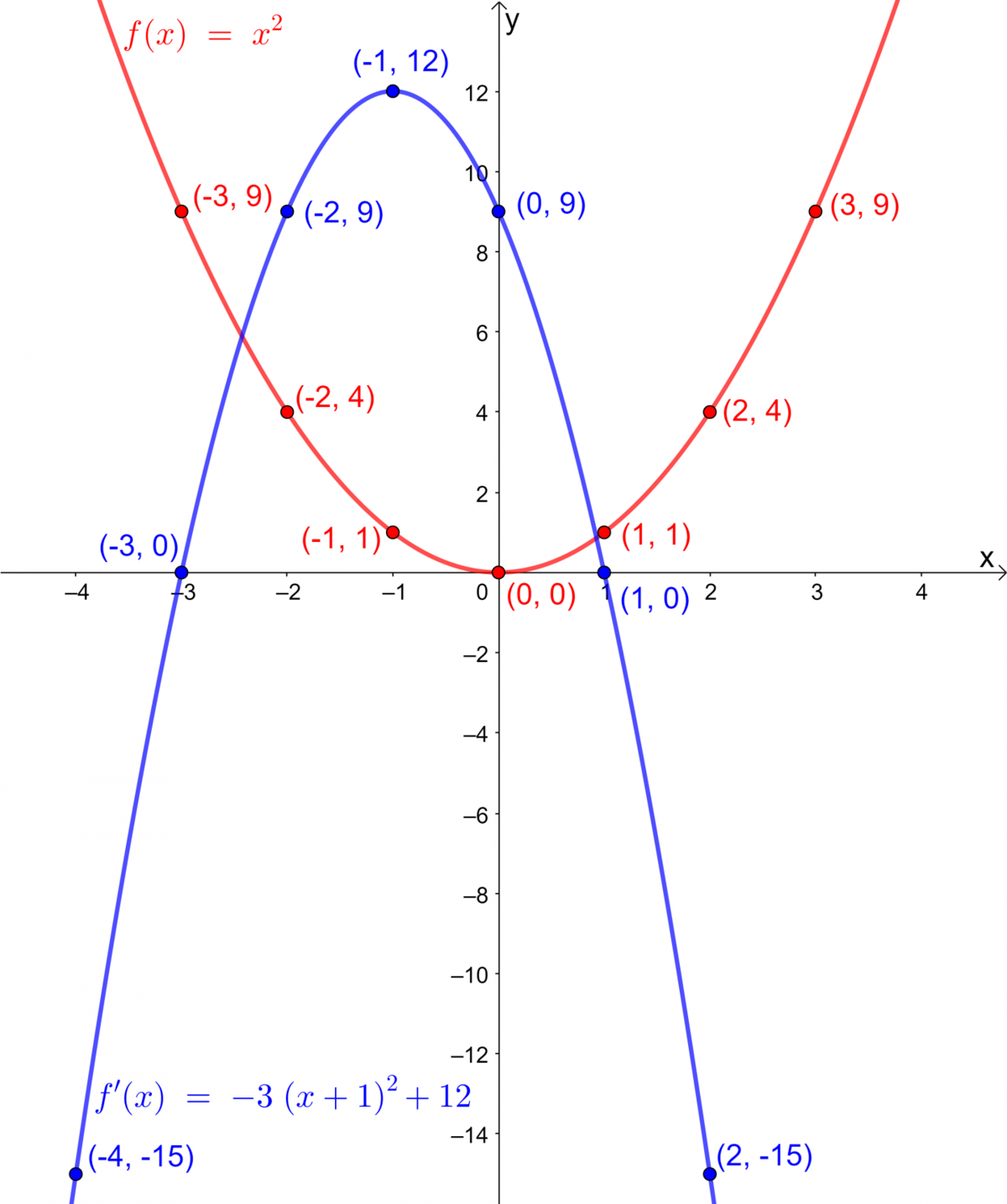
The function drawn in red corresponds to the basic form of the function.
The function drawn in blue corresponds to the function in standard form where |a=-3,\ b=1,\ h=-1,| and |k=12|. It underwent a vertical stretching by a factor of |3|, a reflection across the |x|-axis, a horizontal translation by |1| unit to the left and a vertical translation by |12| units upwards.
How does adding parameters result in the following transformation |(x,y) \mapsto \left(\dfrac{x}{b}+h, ay+k \right)|?
Here is an intuitive proof.
Consider a transformed function |y=af(b(x-h))+k| where |f| is the basic function.
Isolate the part |f(b(x-h))|. ||\begin{align}y &= af(b(x-h))+k\\y-k &= af(b(x-h))\\ \dfrac{y-k}{a} &= f(b(x-h))\end{align}||
Letting |Y=\dfrac{y-k}{a}|, |y| can be isolated.
First, we have |aY=y-k| and finally: |y=aY+k|.
Letting |X=b(x-h)|, |x| can be isolated.
First, we have |\dfrac{X}{b}=x-h| and finally: |x=\dfrac{X}{b}+h|.
Simply note that |X| is the value of the |x|-coordinate in the base function and that after applying the parameters, the result is |x|.
Same thing for |Y| and |y|.