Interest on money can be earned in two different ways: on an investment or a loan. With an investment, the person placing the investment receives an additional sum of money for the amount he or she invests. With a loan, the person who receives the money from the loan has to pay extra when they repay the loan. In both cases, the interest is usually calculated on an annual rate basis.
The ultimate goal of any investment is to make the most money possible when the investment comes to an end (matures).
In mathematical terms, determining the duration of an investment is the same as finding the value of the exponent variable. To do so, follow these steps:
-
Find the equation associated with the situation.
-
Isolate the exponential notation.
-
Switch to logarithmic notation.
-
Isolate the variable.
-
Write the answer as a sentence
Sometimes it is simply a matter of determining the duration of the investment in order to obtain a desired amount.
To ensure a worry-free retirement, a prolific businessman wants to get a future value of |\color{#ec0000}{\$500\,000}| from a current value of |\color{#3387cd}{\$350\,000}.| His attention is caught by the recent compound interest rate of |\color{#3a9a38}{7.89\%}| per year.
If the interest is compounded weekly, how long should he invest his money?
-
Find the equation associated with the situation.
||\begin{align}\color{#ec0000}{C_n} &= \color{#3b87cd}{C_0} \left(1 +\dfrac{\color{#3a9a38}{i}}{\color{#ff55c3}{k}}\right)^n \\[5pt] \color{#ec0000}{500\ 000} &= \color{#3b87cd}{350\ 000} \left(1 +\dfrac{\color{#3a9a38}{0.0789}}{\color{#ff55c3}{52}}\right)^n \\[5pt] \color{#ec0000}{500\ 000} &\approx \color{#3b87cd}{350\ 000} (1.0015)^n \\[5pt] &\text{where} \\ n\! &: \text{number of interest periods}\end{align}||
-
Isolate the exponential notation.
||\begin{align}\dfrac{\color{#ec0000}{500\ 000}}{350\ 000} &\approx \dfrac{\color{#3387cd}{350\ 000}\,(1.0015)^n}{350\ 000} && \text{inverse operation}\\[5pt] 1.4286 &\approx 1.0015^n \end{align}||
-
Switch to logarithmic notation.
||\begin{align} 1.4286 &\approx 1.0015^n \\[5pt] \log_{1.0015}(1.4286) &\approx n && \text{def. of log} \end{align}||
-
Isolate the variable.
||\begin{align}\log_{1.0015}(1.4286) &\approx n \\[5pt] \dfrac{\log_{10}(1.4286)}{\log_{10}(1.0015)} &\approx n && \text{change of base rule} \\[5pt] 237.97 &\approx n \end{align}||
-
Write the answer as a sentence.
He will have to invest his money for 238 weeks to obtain the target future value.
Note that the variable |n| is directly linked to the interest period. If the period is daily, |n| represents the number of interest periods in days; if it is monthly, |n| represents the number of interest periods in months.
The calculation will not be affected by this, but the final answer must take this relationship into account.
When it comes to making a choice, the most advantageous option is always sought. In financial terms, this means maximizing profit or minimizing expenses. Time also has a direct impact on these objectives.
When it comes to making long-term investments in financial institutions, the duration of the investment is generally set at the time of signing. Consider the two following options:
Option 1) Invest |\$15\,000| at an annual compound interest rate of |2.5\%.|
Option 2) Invest |\$12\,000| at an annual compound interest rate of |3.9\%.|
What are the circumstances that favour each choice?
-
Identify the equation of each investment.
||\begin{align} \color{#3b87cd}{\text{Option 1}} &= \color{#3b87cd}{15\ 000\, (1+0.025)^n} \\ \color{#3b87cd}{\text{Option 1}} &= \color{#3b87cd}{15\ 000\,(1.025)^n} \\\\ \color{#ec0000}{\text{Option 2}} &= \color{#ec0000}{12\ 000\,(1+0.039)^n} \\ \color{#ec0000}{\text{Option 2}} &= \color{#ec0000}{12\ 000 \,(1.039)^n} \\ &\text{where} \\ n\!&: \text{number of years invested} \end{align}||
-
Compare the two equations.||\begin{align} \color{#3b87cd}{\text{Option 1}} &= \color{#ec0000}{\text{Option 2}} \\ \color{#3b87cd}{15\ 000\, (1.025)^n}&= \color{#ec0000}{12\ 000 \,(1.039)^n} \end{align}||
-
Solve.
||\begin{align} \dfrac{\color{#3b87cd}{15\ 000(1.025)^n}}{12\ 000}&= \dfrac{\color{#ec0000}{12\ 000(1.039)^n}}{12\ 000}&&\text{inverse operation} \\[5pt] \dfrac{\color{#3b87cd}{1.25(1.025)^n}}{1.025^n} &= \dfrac{\color{#ec0000}{1.039^n}}{1.025^n} && \text{inverse operation} \\[5pt] 1.25 &= \left(\dfrac{1.039}{1.025}\right)^n && \text{properties of exponents} \\[5pt] 1.25 &\approx 1.014 ^n && \text{calculation of the quotient} \\[5pt] \log_{1.014}(1.25) &\approx n && \text{def. of a log} \\[5pt] \dfrac{\log_{10}(1.25)}{\log_{10}(1.014)} &\approx n &&\text{change of base} \\[5pt] 16.05 &\approx n \end{align}||
-
Write the answer as a sentence.
The investment options will have the same value after |16.05| years. Prior to |16.05| years, Option 1 is the most attractive because the current amount of money is higher. If the investment lasts more than |16.05| years, Option 2 is better.

When comparing a situation with an equation, it's always a good idea to model it on the Cartesian plane.
There are certain moments in life when it can be hard to find the financial resources to buy certain items. A car or a house are two examples of this type of purchase. However, financial institutions are willing to lend money to individuals for an annual interest rate that is generally compounded daily. In other words, the interest is calculated every day based on the outstanding amount left to pay.
The purchase price of a house is |\$200\ 000| and the buyer agrees to finance the loan at a |2.89 \%| interest rate, compounded daily. Under these conditions, his monthly payments will be |\$700.|
-
Find the equation to represent this situation.||\begin{align}C_n&=\color{#3b87cd}{C_0}\ \left(1+\dfrac{\color{#3a9a38}{i}}{\color{#ff55c3}{k}}\right)^n\\[5pt] &=\color{#3b87cd}{200\ 000}\ \left(1+\frac{\color{#3a9a38}{0.0289}}{\color{#ff55c3}{365}}\right)^n\\[5pt] &\approx\color{#3b87cd}{200\ 000}\ (1.000\,079)^n\end{align}||
-
Determine the amount of the loan after one interest period.||\begin{align} C_n &= \color{#3b87cd}{200\ 000} \ (1.000\, 079)^n \\ &= \color{#3b87cd}{200\ 000} \ (1.000\, 079)^{30} \\ &\approx 200\ 000 \times 1.002\, 372 \\ &\approx \$200\ 474.54 \end{align}||
-
Determine the new loan amount after the first payment.
||\begin{align} \text{New amount} &= \text{Loan with interest}- \text{Monthly payment} \\ &=200\ 474.54-700 \\ &=\$199\ 774.54 \end{align}||
-
Repeat the procedure for the next month.||\begin{align} C_n &= 199 \ 774.54 \ (1.000\,079)^n \\ &= 199 \ 774.54 \ (1.000\,079)^{30} \\ &\approx \$200 \ 248.54 \end{align}||The remaining loan amount to be repaid after the second payment |= 200\ 248.54 - 700 = \$199\ 548.54.|
Here is a graph to illustrate the situation:
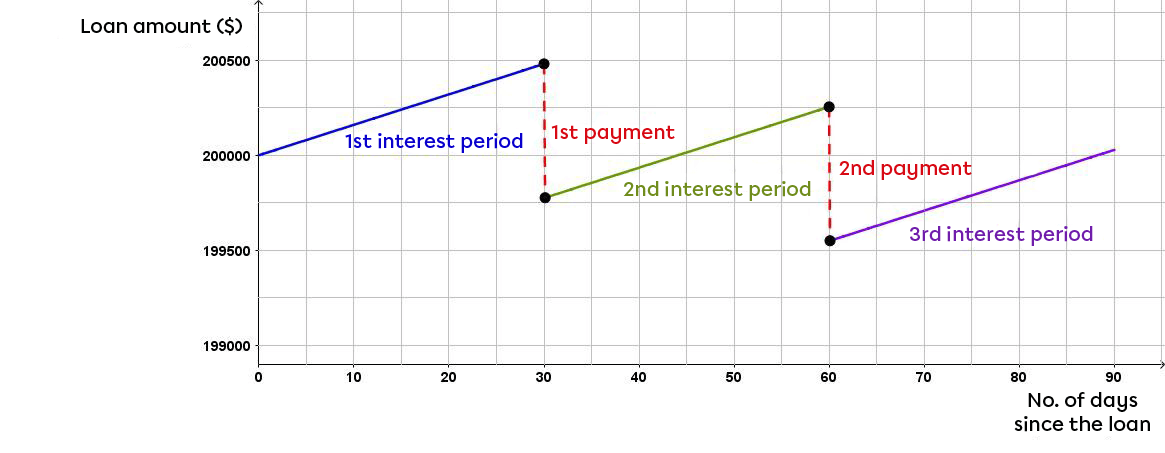
Note that a |\$700| payment per month does not mean that the amount of money borrowed is reduced by |\$700.| This payment is used to cover the interest accrued during the previous interest period and the remainder is used to repay part of the initial loan amount.