Les intérêts sur de l'argent peuvent se manifester de deux façons différentes : un placement ou un prêt. Au niveau du placement, l'individu qui effectue le placement reçoit une somme supplémentaire d'argent pour le montant qu'il investit. En ce qui concerne le prêt, la personne qui reçoit l'argent du prêt doit payer un extra lors du remboursement de son prêt. Dans un cas comme dans l'autre, le tout est généralement calculé à partir d'un taux d'intérêt annuel.
Le but ultime qui se cache derrière un placement ou un investissement est d'obtenir le plus d'argent possible lorsque ce placement ou cet investissement vient à terme.
En terme mathématique, déterminer la durée d'un placement est synonyme de trouver la valeur de la variable qui joue le rôle de l'exposant. Afin de bien orienter sa démarche, on peut suivre les étapes suivantes.
- Déterminer l'équation en lien avec la situation
- Isoler la notation exponentielle
- Transformer l'équation à l'aide de la définition de la notation logarithmique
- Isoler la variable
- Écrire la réponse à l'aide d'une phrase
Dans certains cas, il s'agit seulement de déterminer la durée du placement afin d'obtenir le montant voulu.
Afin de s'assurer d'une retraite sans soucis financier, un prolifique homme d'affaire veut obtenir une valeur future de 500 000 $ à partir d'une valeur actuelle de 350 000 $. Ces temps-ci, les taux d'intérêts composés se chiffrent à 7,89 % par année, ce qui attire son attention.
Si la période d'intérêt est hebdomadaire, pendant combien de temps devrait-il placer son argent?
1. Déterminer l'équation en lien avec la situation
||\begin{align}
\color{red}{C_n} &= \color{blue}{C_0} \left(1 +\frac{\color{green}{i}}{\color{fuchsia}{k}}\right)^n \\\\
\color{red}{500 \ 000} &= \color{blue}{350 \ 000} \left(1 +\frac{\color{green}{0,0789}}{\color{fuchsia}{52}}\right)^n \\\\
\color{red}{500 \ 000} &\approx \color{blue}{350 \ 000} (1,0015)^n \\\\
\small\text{avec} \ n &= \ \small\text{nb de périodes d'intérêt en semaines (hebdomadaire)}\end{align}||
2. Isoler la notation exponentielle
||\begin{align}
\frac{\color{red}{500 \ 000}}{350 \ 000} &\approx \frac{\color{blue}{350 \ 000}}{350 \ 000} (1,0015)^n && \small \text{opération inverse}\\\\
1,4286 &\approx 1,0015^n \end{align}||
3. Transformer l'équation à l'aide de la définition de la notation logarithmique
||\begin{align}
1,4286 &\approx 1,0015^n \\\\
log_{1,0015} \ 1,4286 &\approx n && \small\text{déf. du log} \end{align}||
4. Isoler la variable
||\begin{align}
log_{1,0015} \ 1,4286 &\approx n \\\\
\frac{log_{10} \ 1,4286}{log_{10} \ 1,0015} &\approx n && \small\text{loi du changement de base} \\\\
237,97 &\approx n \end{align}||
5. Écrire la réponse à l'aide d'une phrase
Il devra placer son argent pendant 238 semaines afin d'obtenir la valeur future visée.
Fait à noter, le variable |n| est en lien direct avec la période d'intérêt. Si cette dernière est quotidienne, alors |n| représente le nombre d'intérêt en jours; si elle est mensuelle, alors |n| représente le nombre de périodes d'intérêt en mois.
Les calculs n'en seront pas affectés, mais l'écriture de la réponse finale doit mettre de l'avant cette relation.
Lorsque vient le temps de faire un choix, on est toujours à la recherche du choix le plus avantageux. Dans un cadre financier, cette façon de penser vise un profit maximum ou un minimum de dépense. De plus, le temps peut avoir un impact direct sur ces objectifs.
Lorsque vient le temps de faire des placements à long terme dans les institutions financières, la durée de ces derniers sont généralement établies à la signature. Parmi les deux options suivantes,
Option 1) Placer un montant de 15 000 $ à un taux d’intérêt composé annuellement de 2,5 %;
Option 2) Placer un montant de 12 000 $ à un taux d’intérêt composé annuellement de 3,9 %.
Décris les circonstances qui favorisent chacun des choix.
1) Trouver l’équation pour chacun des placements
||\begin{align} \color{blue}{\small \text{option 1}} &= \color{blue}{15 \ 000 \ (1+0,025)^n} \\ \color{blue}{\small \text{option 1}} &= \color{blue}{15 \ 000 \ (1,025)^n} \\\\ \color{red}{\small \text{option 2}} &= \color{red}{12 \ 000 \ (1+0,039)^n} \\ \color{red}{\small \text{option 2}} &= \color{red}{12 \ 000 \ (1,039)^n} \\ \small\text{avec} \ n \ & : \ \small\text{nb d’années du placement} \end{align}||
2) Comparer les deux équations
||\begin{align} \color{blue}{\small \text{option 1}} &= \color{red}{\small \text{option 2}} \\ \color{blue}{15 \ 000 \ (1,025)^n}&= \color{red}{12 \ 000 \ (1,039)^n} \end{align}||
3) Résoudre
||\begin{align} \frac{\color{blue}{15 \ 000}}{12 \ 000} \ \color{blue}{(1,025)^n}&= \frac{\color{red}{12 \ 000}}{12 \ 000} \ \color{red}{ (1,039)^n} && \small\text{opération inverse} \\\\ 1,25 \frac{\color{blue}{1,025^n}}{1,025^n} &= \frac{\color{red}{1,039^n}}{1,025^n} && \small\text{opération inverse} \\\\ 1,25 &= \left(\frac{1,039}{1,025}\right)^n && \small\text{propriété des exposants} \\\\ 1,25 &\approx 1,014 ^n && \small\text{calcul du quotient} \\\\ log_{1,014} \ 1,25 &\approx n && \small\text{déf. du log} \\\\ \frac{log_{10} \ 1,25}{log_{10} \ 1,014} &\approx n && \small\text{changement de base} \\\\ 16,05 &\approx n \end{align}||
4) Écrire la réponse à l’aide d’une phrase
Les deux placements auront la même valeur après |16,05| années. Avant |16,05| ans, c’est l’option 1 qui est la plus intéressante puisque le montant actuel est plus élevé. Si le placement dure plus de |16,05| ans, c’est l’option 2 qui est à privilégier.
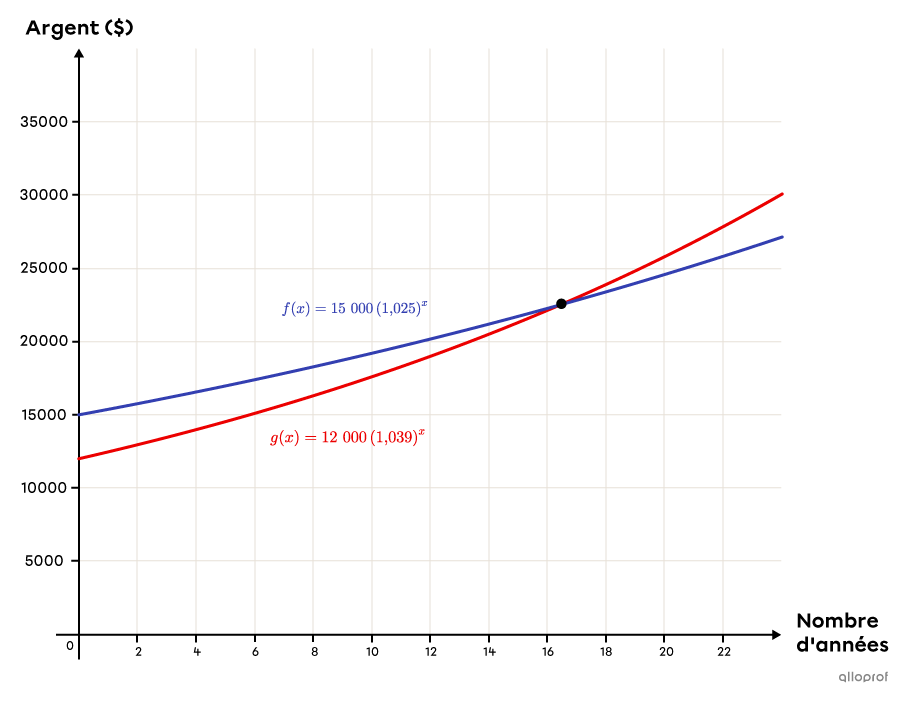
Lorsque vient le temps de comparer une situation que l’on peut résumer en une équation, il est toujours idéal de modéliser le tout par le biais du plan cartésien.
Il existe certains moments dans la vie où il est difficile d’avoir les ressources financières suffisantes pour faire l’achat de divers produits. Une voiture, une maison sont des exemples de ce type d’achat. Par contre, il existe des institutions financières qui consentent à prêter de l’argent au particulier moyennant un taux d’intérêt annuel qui est généralement composé quotidiennement. En d’autres mots, les intérêts sont calculés à chaque jour sur le montant qu’il reste à payer.
Supposons qu’une maison est achetée pour |200 \ 000 \ \$| et que l’acheteur accepte de financer ce prêt avec un taux d’intérêt de |2,89 \ \%| composé quotidiennement. Selon ces conditions, il sait que ses paiements mensuels seront de |700 \ \$|.
1) Équation qui représente cette situation
||\begin{align}C_n&=\color{blue}{C_0}\ \left(1+\frac{\color{green}{i}}{\color{fuchsia}{k}}\right)^n\\\\&=\color{blue}{200\ 000}\ \left(1+\frac{\color{green}{0,0289}}{\color{fuchsia}{365}}\right)^n\\\\&\approx\color{blue}{200\ 000}\ (1{,}000\ 079)^n\end{align}||
2) Déterminer le montant du prêt après une période d’intérêt
||\begin{align} C_n &= \color{blue}{200\ 000} \ (1{,}000\ 079)^n \\ &= \color{blue}{200 \ 000} \ (1{,}000\ 079)^{30} \\ &\approx 200\ 000 \times 1{,}002\ 372 \\ &\approx 200\ 474{,}54 \end{align}||
3) Déterminer le nouveau montant du prêt après le premier versement
||\begin{align}\text{nouveau montant}&=\text{prêt avec intérêt}&&-&&\text{paiement mensuel}\\&=200\ 474{,}54&&-&&700\\&=199\ 774{,}54\end{align}||
4) Répéter la procédure pour le prochain mois
||\begin{align}C_n&=199\ 774{,}54\ (1{,}000\ 079)^n\\&=199\ 774{,}54\ (1{,}000\ 079)^{30}\\&\approx200\ 248{,}54\end{align}||
Ainsi, le montant du prêt qui reste à rembourser suite au deuxième versement |= 200 \ 248,54 – 700 = 199 \ 548,54 \ \$|
Voici un graphique qui permet de bien illustrer le tout :
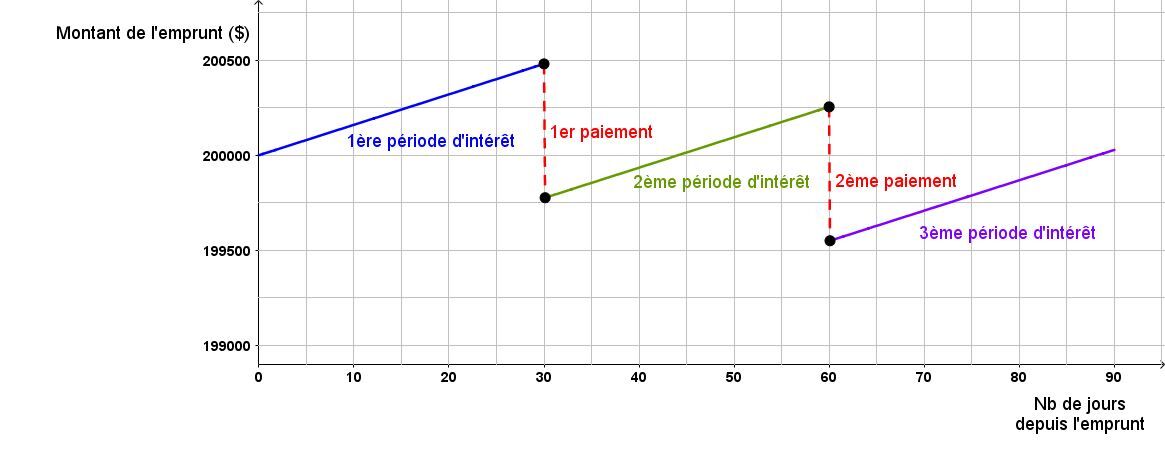
Comme on peut le constater, un paiement de |700 \ \$| par mois ne signifie pas que le montant emprunter diminue de |700 \ \$|. En effet, ce paiement sert à couvrir les intérêts encourus durant la dernière période d’intérêt et le reste sert à rembourser une partie du montant emprunté.