Solving problems involving a logarithmic function requires both knowing how the function works and understanding how to solve an equation or inequality out of context. Consult the following concept sheet if needed: Solving a Logarithmic Equation or Inequality.
When athletes first begin to train, they usually make rapid progress. After a while, it is often said that they have “plateaued”. In reality, athletes continue to improve, but their progress becomes less and less noticeable. For this reason, an athlete's performance can be modeled by a logarithmic function.
The following graph shows the time it takes for an amateur runner to complete a half-marathon depending on the number of weeks they train.
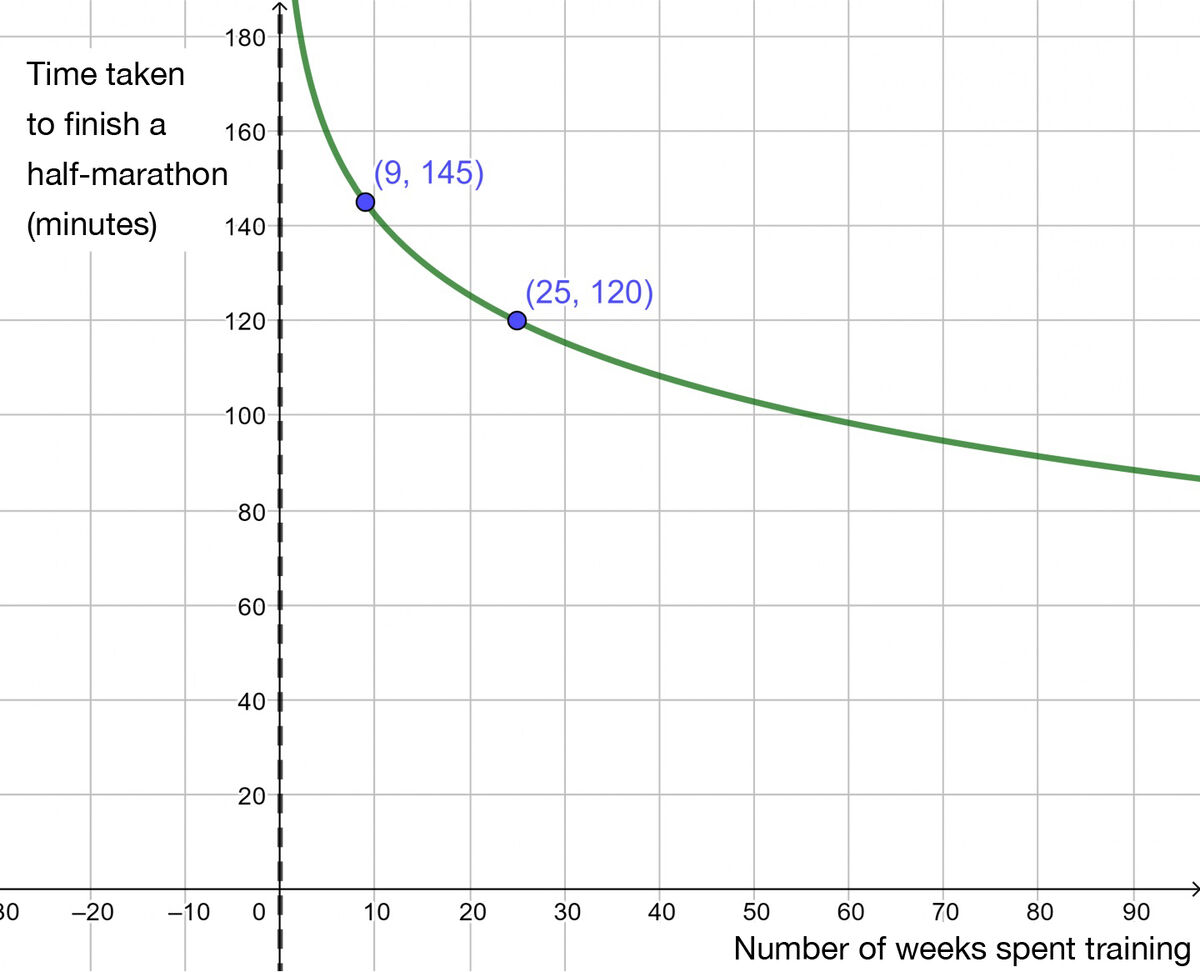
a) What is the approximate time of their half-marathon after |1| full year of training?
b) If the trend continues to follow the same pattern, after how many weeks of training can a runner expect to complete a half-marathon in less than |1| hour and |30| minutes?
-
Identify the variables
|x|: Number of weeks of training
|f(x)|: Time required to do a half-marathon (minutes) -
Find the equation
Note that there is an asymptote at |x=0.| Essentially, this means that the athlete was not able to complete a half-marathon when they started training. As for the equation, this means that |h=0.|
Note from the graph that a decreasing curve is located to the right of the asymptote. This means that |a>0,| |b>0,| and |0<c<1.|1.| p="">
It is possible to assign the value of |1| to |a| and use the equation |f(x)=\log_c b(x-h)| or the equation |f(x)=\log_c (x-h)+k.| The 2 equations are equivalent and make it possible to obtain the same results for questions a) and b). For this example, use the equation |f(x)=\log_c b(x-h).| The method using the equation |f(x)=\log_c (x-h)+k| is shown in the section “For more details” following this example.-
Replace |h| with the value of the asymptote ||\begin{align} y &= \log_c b(x-\color{blue}{h}) \\y &= \log_c b(x-\color{blue}{-0}) \\y &= \log_c bx \\ \end{align}||
-
Substitute in each of the points to create a system of equations ||\begin{align} 1^{\text{st}} &\text{ coordinate pair : }(\color{green}{9},\color{red}{145}) &&2^\text{nd} \text{ coordinate pair : }(\color{green}{25},\color{red}{120}) \\\\ \color{red}{y} &= \log_c b\color{green}{x} && \color{red}{y} = \log_c b\color{green}{x} \\\\ \color{red}{145} &= \log_c \color{green}{9}b && \color{red}{120} = \log_c \color{green}{25}b && \text{Substitute in }\color{green}{x} \text{ and } \color{red}{y} \\\\ c^{145} &=9b && c^{120} =25b && \text{Use the exponent laws } \\\\ \frac{c^{145}}{9} &= b && \frac{c^{120}}{25} = b && \text{Isolate }b\end{align}||
-
Determine the value of parameter |c| using the comparison method ||\begin{align} b & = b \\\\ \dfrac{c^{145}}{9} & = \dfrac{c^{120}}{25} \\\\ \dfrac{c^{145}}{c^{120}} & = \dfrac{9}{25} \\\\ c^{25} & = \dfrac{9}{25} && \text{Laws of exponents} \\\\ \sqrt[25]{c^{25}}& = \sqrt[25]{\dfrac{9}{25}} \\\\ c & \approx 0.96\end{align}||
-
Use one of the two points provided to find the value of the parameter |b| ||\begin{align} b &= \dfrac{c^{145}}{9} = \dfrac{0.96^{145}}{9} \approx 0.000\ 3\\ b &= \dfrac{c^{120}}{25} = \dfrac{0.96^{120}}{25} \approx 0.000\ 3 \end{align}||
-
The equation is therefore |f(x)=\log_{0.96}0.000\ 3x.|
a) Approximately what should the runner’s half-marathon time be after |1| full year of training?
The objective is to find the value of |f(52),| that is, the time it takes to do a half-marathon after |1| year of training, or |52| weeks. ||\begin{align} f(x) &= \log_{0.96}0.000\ 3x\\ f(52) &= \log_{0.96}0.000\ 3(52)\\ &= \log_{0.96}0.015\ 6\\ &\approx 101.9\ \text{minutes}\end{align}||
Answer : After a year of training, the athlete should complete their half-marathon in about |1| hour and |42| minutes.
b) If they continue to follow the same schedule, after how many weeks of training can the runner expect to complete the half marathon in less than |1| hour and |30| minutes?
This time, the objective is to find the time required to complete a half-marathon in less than |1| hour and |30| minutes, so |90| minutes. The value of the logarithm must be smaller than |90|, which means |90| must be greater than |(>)| the value of the logarithm. Use the following equation. ||90>\log_{0.96}0.000\ 3x||
Change the greater than sign to an equal sign. ||90=\log_{0.96}0.000\ 3x||
Rewrite the equation to its exponent form. ||90 = \log_{0.96}0.000\ 3x \ \Longleftrightarrow \ 0.96^{90}=0.000\ 3x||
Solve the equation. ||\begin{align} 0.96^{90} &= 0.000\ 3x \\ \frac{0.96^{90}}{0.000\ 3} &= \frac{0.000\ 3x}{0.000\ 3}\\ 84.58 &\approx x \end{align}||
The answer can be interpreted by observing the graph.
Answer: After |84.58| weeks of training, the runner will be able to finish a half-marathon in |1| hour and |30| minutes. Knowing that with more training results in a lower running time, it is easy to see that the runner will have to train |85| weeks or more to run the half-marathon in less than |1| hour and |30| minutes (roughly |1| year and |8| months of training).
To answer the questions in the previous example, it's possible to use the formula |f(x)=\log_c (x-h)+k| to find the equation. Here's how.
-
Replace |h| with the value of the asymptote ||\begin{align} f(x) &= \log_c (x-\color{blue}{h})+k \\f(x) &= \log_c (x-\color{blue}{-0})+k \\f(x) &= \log_c x+k \\ \end{align}||
-
Substitute in each of the points to create a system of equations ||\begin{align} 1^{\text{st}} &\text{ coordinate pair: }(\color{green}{9},\color{red}{145}) &&2^\text{nd} \text{ coordinate pair: }(\color{green}{25},\color{red}{120}) \\\\ \color{red}{f(x)} &= \log_c b\color{green}{x} && \color{red}{f(x)} = \log_c b\color{green}{x} \\\\ \color{red}{145} &= \log_c \color{green}{9}+k && \color{red}{120} = \log_c \color{green}{25}+k && \text{Substitute in }\color{green}{x} \text{ and } \color{red}{y} \\\\ 145&-\log_c 9 = k && 120-\log_c 25 = k && \text{Isolate }k\end{align}||
-
Determine the value of parameter |c| using the comparison method ||\begin{align} k & = k \\\\ 145-\log_c9 &= 120-\log_c 25 \\\\ 25 & = \log_c 9 - \log_c25 \\\\ 25 &= \log_c \left(\dfrac{9}{25}\right) && \text{Law of logarithms}\\\\ c^{25} &= \dfrac{9}{25} && \text{Use exponent laws} \\\\ \sqrt[25]{c^{25}}& = \sqrt[25]{\frac{9}{25}} && \text{Isolate c} \\\\ c & \approx 0.96 \end{align}||
-
Use one of the two points provided to find the value of the parameter |k| ||k = 145-\log_{0.96} 9 \approx 198.8||
Therefore, the equation is |f(x)=\log_{0.96}x+198.8.|
The equation is equivalent to the one found previously. To prove it, we will use it to answer questions a) and b).
a)
||\begin{align} f(x) &= \log_{0.96}x + 198.8 \\ f(52) &= \log_{0.96}(52) + 198.8 \\ &\approx 102\ \text{minutes} \end{align}||
Taking the rounding into consideration, this solution is equivalent to the one obtained with the other formula.
b)
The inequality is the following. ||90 > \log_{0.96}x+198.8||
Change the greater than sign into an equal sign. || 90 = \log_{0.96}x + 198.8||
Isolate the logarithm. ||-108.8 = \log_{0.96}x||
Rewrite the equation using exponential laws and calculate |x.| ||\begin{align} -108.8 = \log_{0.96}x \ \Longleftrightarrow \ 0.96^{-108.8} &= x \\ 84.9 &\approx x \end{align}||
Once again, after rounding, the answer is equivalent to the one obtained using the other formula.
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction logarithmique de façon interactive, consulte la MiniRécup suivante.
