Solving a problem involving a quadratic (or second-degree polynomial) function requires understanding all the properties of a quadratic function and knowing how to solve an equation out of context. Consult the following concept sheet if needed: Solving a Second-degree Equation or Inequality.
The kinetic energy of an object, denoted |E_k,| is the energy that an object possesses due to its motion. The formula for calculating the kinetic energy of an object as a function of its speed is a quadratic function. ||\begin{align} E_k = \frac{1}{2}&mv^2 \\\\ \text{where} \quad E_k &: \text{kinetic energy (J)}\\ m\ &: \text{mass of the object (kg)} \\ v\ \ &: \text{speed of the object (m/s)}\end{align}||
a) What is the kinetic energy of a tennis ball that weighs |58| grams and moves at a speed of |198\ \text{km/h}|?
b) What is the speed in |\text{km/h}| of a golf ball weighing |44| grams if it has the same kinetic energy as the tennis ball in question a)?
a)
To answer question a), use the formula. To calculate the kinetic energy, first convert the mass of the ball into kilograms, since this is the unit of measurement of |m| for the formula for kinetic energy. |58\ \text{g}=0.058\ \text{kg}|
||\begin{align} E_k &= \frac{1}{2}\color{blue}{m}v^2 \\ E_k &= \frac{1}{2}\color{blue}{(0.058)}v^2 \\ E_k &=0.029 v^2 \end{align}||
Now, we want to know the value of |E_k| when |v=198\ \text{km/h}|. Before replacing |v| with the actual speed in the equation of the function, first convert the km/h to m/s. ||\begin{align} 198\ \frac{\text{km}}{h} &= 198\ 000\ \frac{\text{m}}{h} \times \frac{1\ \text{h}}{3\ 600\ \text{s}} \\ &= 55\ \frac{\text{m}}{s} \end{align}||
Finally, calculate |E_k| when |v=55|.||\begin{align} E_k &= 0.029\color{green}{v}^2 \\ &= 0.029\color{green}{(55)}^2 \\&= 87.725\ \text{joules} \end{align}||
Answer: |E_k=87.725\ \text{joules}|
b)
Be careful: here the equation is not the same as in question a), because the mass of the ball is not the same. In this question, |m=44\ \text{g}=0.044\ \text{kg}|. The formula is therefore:||\begin{align} E_k &= \frac{1}{2}\color{blue}{m}v^2 \\ E_k &= \frac{1}{2}\color{blue}{(0.044)}v^2 \\ E_k &=0.022 v^2 \end{align}||
Now we want to know the value of |v| when |E_k=87.725\ \text{joules}|. Replace |E_k| with |87.725| and isolate |v|.||\begin{align} \color{brown}{E_k} &= 0.022v^2 \\ \color{brown}{87.725} &= 0.022v^2 \\ \frac{87.725}{\color{red}{0.022}} &= \frac{0.022v^2 }{\color{red}{0.022}} \\ 3\ 987.5 &= v^2 \\ \sqrt{3\ 987.5} &= \sqrt{v^2} \\ 63.15\ \text{m/s} &\approx v \end{align}||
All that is left to do is convert the answer from m/s to km/h. ||\begin{align} 63.15\ \frac{\text{m}}{\text{s}} \times \frac{3\ 600\ \text{s}}{1\ \text{h}} &= 227\ 340\ \frac{\text{m}}{\text{h}} \\ &= 227.34\ \frac{\text{km}}{\text{h}} \end{align}||
Answer: The golf ball is moving at a speed of |227.34\ \text{km/h}.|
The problem is represented in the following Cartesian plane.
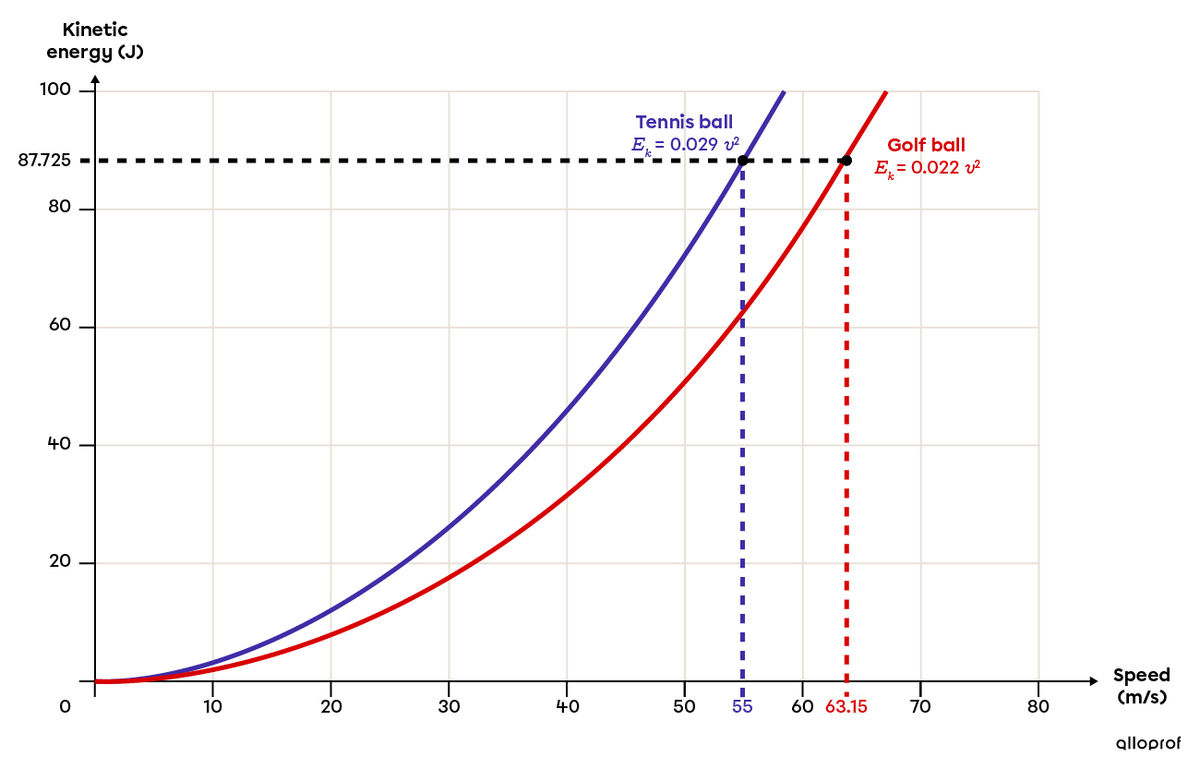
Only the first quadrant is represented because neither the speed nor the energy can be negative.
Notice that the kinetic energy of the tennis ball increases more rapidly since its mass is greater, which means that the parameter |a| of the function is greater. This is why a golf ball must be moving with greater speed than a tennis ball to have the same kinetic energy, confirming our results.
A stock listed on the stock exchange reaches a minimum value of |\$ 4.00| six months after being listed on the stock exchange. The function that represents the decrease in the value of the stock during the first six months after being listed is a quadratic function.
a) If the stock was valued at |\$ 6.00| when it was first listed, what is its value four months later?
b) At what point in the first six months did the stock reach a value of |\$ 5.00|?
It is very important to define the variables.
|x|: number of months since the share was listed on the stock market
|y|: share value in |$|
The statement from the word problem confirms that the function passes through the point |(6,4)| which corresponds to the minimum value of the function.
a)
The problem says that the function passes through the point |(0,6).|
To answer the question, first determine the equation of the function. The minimum of the function is known, that is, its vertex |(h,k)=(6,4).| Additionally, a second point |(0,6)| is also known. Use the vertex form |y=a(x-h)^2+k| to determine the equation.
Find the value of the parameter |a| by substituting in the known values in the equation. ||\begin{align}y&=a(x-h)^2+k \\6&=a(0-6)^2+4\\6&=a(-6)^2+4\\6&=36a + 4\\2 &= 36a\\ \displaystyle \frac{1}{18}&=a \end{align}|| So, the equation of the function is |y=\displaystyle \frac{1}{18}(x-6)^2+4.| To answer the question, simply replace |x| with |4| to find the value of |y.| ||\begin{align}y&=\displaystyle \frac{1}{18}(4-6)^2 + 4\\y&= \displaystyle \frac{1}{18}(-2)^2+4\\y&=\displaystyle \frac{1}{18} (4) + 4\\y&= \displaystyle \frac{2}{9} + 4\\y&=\displaystyle \frac{38}{9} \approx 4.22\end{align}|| Answer: Four months after being listed, the stock is valued at |\$ 4.22| per share.
b)
To determine after how many months the stock is valued at |\$ 5.00,| replace |y| with |5|, and then isolate |x.| ||5=\displaystyle \frac{1}{18}(x-6)^2+4||
The left side of the equation must be equal to 0. ||0=\displaystyle \frac{1}{18}(x-6)^2-1||
The formula |x_{1,2} = h \pm \displaystyle \sqrt{-\frac{k}{a}}| can be used to find the missing value.
In this case, |a=\dfrac{1}{18},h=6,| and |k=-1.| ||\begin{align}x_{1,2} &= \displaystyle 6 \pm \sqrt{-\frac{-1}{\frac{1}{18}}}\\x_{1,2} &= 6 \pm \sqrt{18}\end{align}||
Then, separate the formula into two parts. ||\begin{align}x_1 &= 6 + \sqrt{18} \approx 10.24\\x_2 &= 6 - \sqrt{18} \approx 1.76 \end{align}||
So, to answer the question, disregard the first value found and only keep the second value.
Answer: The value of the share is |\$ 5.00| a little over a month after being listed.
In the previous example, there were only equations and not inequalities. A final question using inequalities could be: "During what time interval was the stock's value less than |\$ 5.00|?"
To find out how to solve this kind of question, consult the following concept sheet: Solving a Single-variable Second-degree Polynomial Inequality.
The amount of water in the tank of a wastewater treatment plant varies depending on the time of day. This situation can be modeled using a quadratic function. The plant's tank is filled to its capacity of |25\ 000\ \text{L}| at noon. It is empty at 8 p.m (20:00).
a) What is the equation in standard form associated with the amount of water in the reservoir depending on the time of day?
b) At what times is the factory tank filled with |15\ 000\ \text{L}|?
It is very important to define the variables.
|x|: time of day (in hours)
|y|: amount of water in the tank
It is possible to find two points belonging to the function. These are the points |(12, 25\ 000)| and |(20,\ 0).|
The point |(12, 25\ 000)| corresponds to the maximum value of the function.
a)
To find the equation of the function modeling this situation, use the vertex form of the quadratic function. The point |(12, 25\ 000)| being the vertex, the vertex form is best for finding the equation.
The vertex form of the quadratic function is |y=a(x-h)^2+k.| In this situation, |(h,k)=(12, 25\ 000)| and |(x,y)=(20,0).| Then replace these parameters and variables in the equation. ||y=a(x-h)^2+k \rightarrow 0=a(20-12)^2+25\ 000||
Now isolate the value of |a.| || \begin{align}0&=a(20-12)^2 + 25\ 000 \\ 0&= a(8)^2 + 25\ 000 \\ 0&= 64a + 25\ 000 \\ -25\ 000 &= 64a \\ -390.625&= a \end{align}||
So, the equation of the function in vertex form is |y=-390.625(x-12)^2 + 25\ 000.|
All that is left to do is to convert from the vertex form to the general form using algebraic manipulations. ||\begin{align}y&=-390.625(x-12)^2+25\ 000 \\ y&= -390.625(x-12)(x-12) +25\ 000 \\ y&= -390.625(x^2-24x+144) + 25\ 000 \\ y&= -390.625x^2 + 9\ 375x - 56\ 250 + 25\ 000 \\ y&= -390.625x^2 + 9\ 375x - 31\ 250 \end{align}||
Answer: The general form is therefore |y=-390.625x^2 + 9\ 375x - 31\ 250.|
b)
To determine at what times the tank contains |15\ 000\ \text{L},| replace |y| with |15\ 000| in the equation. ||15\ 000=-390.625x^2+9\ 375x-31\ 250||
To solve such an equation, make the left side equal to 0. ||\begin{align} 15\ 000 &= -390.625x^2 + 9\ 375x - 31\ 250 \\ \Rightarrow \quad 0 &=-390.625x^2 + 9\ 375x-46\ 250 \end{align}||
Now, in order to find the solutions of this equation, use the quadratic formula: |\displaystyle x_{1,2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a}.|
In this case, |a=-390.625, b=9\ 375,| and |c=-46\ 250|. ||\begin{align}\displaystyle x_{1,2} &= \frac{-9\ 375 \pm \sqrt{9\ 375^2 - 4\times -390.625 \times -46\ 250}}{2 \times -390.625} \\ \displaystyle x_{1,2} &= \frac{-9\ 375 \pm \sqrt{15\ 625\ 000}}{-781.25}\end{align}||
Then, separate the formula into two parts. ||\begin{align}\displaystyle x_1 &= \frac{-9\ 375 + \sqrt{15\ 625\ 000}}{-781.25} \approx 6.94\\ \displaystyle x_2 &= \frac{-9\ 375 - \sqrt{15\ 625\ 000}}{-781.25} \approx 17.06 \end{align}||
To give the answer to the question, convert the two values |x_1| and |x_2| into hours and minutes.
-
|x_1| corresponds to |6| hours and |56| minutes. Essentially, |0.94 \times 60 = 56.4| minutes, which can be rounded to |56| minutes.
-
|x_2| corresponds to |17| hours and |4| minutes. Essentially, |0.06 \times 60 = 3.6| minutes, which can be rounded to |4| minutes.
Answer: The water level of the tank will be |15\ 000\ \text{L}| at 6:56 a.m. and 5:04 p.m (17:04).
