Pour résoudre un problème où intervient une fonction polynomiale du second degré, il faut connaitre tous les rouages de cette fonction et il faut connaitre les façons de résoudre une équation hors contexte. Tu peux consulter la fiche suivante au besoin : Résoudre une équation ou une inéquation de degré 2.
L’énergie cinétique d’un objet, notée |E_k,| est l’énergie que celui-ci possède en fonction de son mouvement. La formule qui permet de calculer l’énergie cinétique d’un objet en fonction de sa vitesse est une fonction polynomiale de degré 2. La règle est la suivante : ||\begin{align} E_k = \frac{1}{2}&mv^2 \\\\ \text{où} \quad E_k &: \text{énergie cinétique (J)}\\ m\ &: \text{masse de l’objet (kg)} \\ v\ \ &: \text{vitesse de l’objet (m/s)}\end{align}||
a) Quelle est l’énergie cinétique d’une balle de tennis de |58| grammes qui se déplace à |198\ \text{km/h}|?
b) Quelle est la vitesse de déplacement en |\text{km/h}| d’une balle de golf de |44| grammes si elle possède la même énergie cinétique que la balle de tennis de la question a)?
a)
Pour répondre à la question a), il faut connaitre la règle. Pour ce faire, il faut convertir la masse de la balle en kg, car c'est l’unité de mesure de |m| employée dans la règle de l'énergie cinétique. |58\ \text{g}=0{,}058\ \text{kg}|
||\begin{align} E_k &= \frac{1}{2}\color{blue}{m}v^2 \\ E_k &= \frac{1}{2}\color{blue}{(0{,}058)}v^2 \\ E_k &=0{,}029 v^2 \end{align}||
On cherche maintenant la valeur de |E_k| lorsque |v=198\ \text{km/h}|. Pour remplacer |v| par la vitesse dans la règle de la fonction, il faut d’abord convertir les km/h en m/s. ||\begin{align} 198\ \frac{\text{km}}{h} &= 198\ 000\ \frac{\text{m}}{h} \times \frac{1\ \text{h}}{3\ 600\ \text{s}} \\ &= 55\ \frac{\text{m}}{s} \end{align}||
Finalement, on calcule |E_k| lorsque |v=55|. ||\begin{align} E_k &= 0{,}029\color{green}{v}^2 \\ &= 0{,}029\color{green}{(55)}^2 \\&= 87{,}725\ \text{joules} \end{align}||
Réponse : |E_k=87{,}725\ \text{joules}|
b)
Attention, ici la règle n’est pas la même que pour la question a), car la masse de la balle n’est pas la même. Pour cette question, |m=44\ \text{g}=0{,}044\ \text{kg}|. La règle est donc : ||\begin{align} E_k &= \frac{1}{2}\color{blue}{m}v^2 \\ E_k &= \frac{1}{2}\color{blue}{(0{,}044)}v^2 \\ E_k &=0{,}022 v^2 \end{align}||
Maintenant, on cherche la valeur de |v| lorsque |E_k=87{,}725\ \text{joules}|. On remplace |E_k| par |87{,}725| et on isole |v|. ||\begin{align} \color{brown}{E_k} &= 0{,}022v^2 \\ \color{brown}{87{,}725} &= 0{,}022v^2 \\ \frac{87{,}725}{\color{red}{0{,}022}} &= \frac{0{,}022v^2 }{\color{red}{0{,}022}} \\ 3\ 987{,}5 &= v^2 \\ \sqrt{3\ 987{,}5} &= \sqrt{v^2} \\ 63{,}15\ \text{m/s} &\approx v \end{align}||
Il ne reste qu’à convertir les m/s en km/h. ||\begin{align} 63{,}15\ \frac{\text{m}}{\text{s}} \times \frac{3\ 600\ \text{s}}{1\ \text{h}} &= 227\ 340\ \frac{\text{m}}{\text{h}} \\ &= 227{,}34\ \frac{\text{km}}{\text{h}} \end{align}||
Réponse : La balle de golf se déplace à une vitesse de |227{,}34\ \text{km/h}.|
On peut représenter la situation dans le plan cartésien suivant :
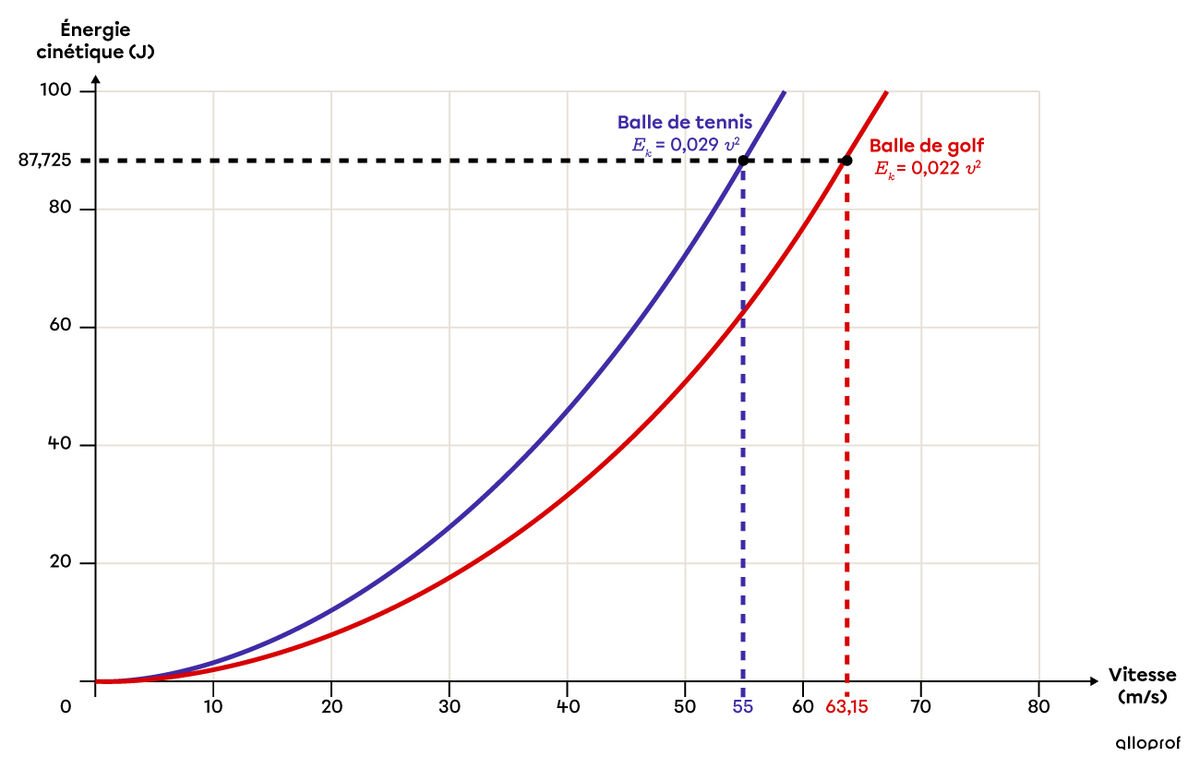
On ne représente que le premier quadrant parce que ni la vitesse ni l’énergie ne peuvent être négatives.
On remarque que l’énergie cinétique de la balle de tennis augmente plus rapidement puisque sa masse est plus grande, ce qui fait que le paramètre |a| de la fonction est plus grand. C’est pour cette raison qu’une balle de golf doit voyager avec une plus grande vitesse qu’une balle de tennis pour posséder la même énergie cinétique, ce qui confirme nos résultats.
Une action cotée à la bourse atteint une valeur minimale de 4,00 $ six mois après son émission à la Bourse. La fonction qui décrit la baisse de la valeur de l'action durant les six premiers mois suivant son émission est une fonction polynomiale du second degré.
a) Si l'action possédait une valeur de 6,00 $ au moment de son émission, combien valait-elle quatre mois plus tard?
b) À quel moment, au cours des six premiers mois, l'action a-t-elle atteint une valeur de 5,00 $?
Il est très important de définir les variables :
|x:| nombre de mois écoulés depuis l'émission de l'action à la Bourse
|y:| valeur de l'action en $
L'énoncé du problème permet d'affirmer que la fonction passe par le point |(6,4)| qui correspond au minimum de la fonction.
a)
On peut affirmer que la fonction passe par le point |(0,6).|
Pour répondre à la question, il faut déterminer l'équation de la fonction. Connaissant le minimum de la fonction, on connait aussi le sommet |(h,k)=(6,4).| De plus, on connait un second point |(0,6).| Il sera donc nécessaire d'utiliser la forme canonique |y=a(x-h)^2+k| pour déterminer l'équation.
On trouve la valeur du paramètre |a| en remplaçant les valeurs connues dans l'équation. ||\begin{align}y&=a(x-h)^2+k \\6&=a(0-6)^2+4\\6&=a(-6)^2+4\\6&=36a + 4\\2 &= 36a\\ \displaystyle \frac{1}{18}&=a \end{align}||
Ainsi, l'équation de la fonction est |y=\displaystyle \frac{1}{18}(x-6)^2+4.|
Pour répondre à la question, il suffit de remplacer |x| par |4| et de trouver la valeur de |y.| ||\begin{align}y&=\displaystyle \frac{1}{18}(4-6)^2 + 4\\y&= \displaystyle \frac{1}{18}(-2)^2+4\\y&=\displaystyle \frac{1}{18} (4) + 4\\y&= \displaystyle \frac{2}{9} + 4\\y&=\displaystyle \frac{38}{9} \approx 4{,}22\end{align}||
Réponse : Quatre mois après son émission, l'action vaut |4{,}22\ $.|
b)
Pour déterminer après combien de mois l'action vaut |5{,}00\ $,| il faut remplacer |y| par |5|, puis isoler |x.| ||5=\displaystyle \frac{1}{18}(x-6)^2+4||
Il faut maintenant rendre l'équation égale à 0. ||0=\displaystyle \frac{1}{18}(x-6)^2-1||
On peut utiliser la formule |x_{1,2} = h \pm \displaystyle \sqrt{-\frac{k}{a}}| pour trouver la valeur recherchée.
Dans ce cas, |a=\dfrac{1}{18},h=6| et |k=-1.| ||\begin{align}x_{1,2} &= \displaystyle 6 \pm \sqrt{-\frac{-1}{\frac{1}{18}}}\\x_{1,2} &= 6 \pm \sqrt{18}\end{align}||
On sépare la formule en deux parties. ||\begin{align}x_1 &= 6 + \sqrt{18} \approx 10{,}24\\x_2 &= 6 - \sqrt{18} \approx 1{,}76 \end{align}||
Ainsi, pour répondre à la question, on laisse tomber la première valeur trouvée. On ne conserve que la seconde valeur.
Réponse : La valeur de l'action est de |5{,}00\ $| un peu plus d'un mois après son émission.
Dans l'exemple précédent, il n'y avait que des équations et non pas des inéquations. Une dernière sous-question qui aurait fait appel aux inéquations pourrait être : « Pendant quel intervalle de temps la valeur de l'action était-elle de moins de 5,00 $? »
Pour savoir comment répondre à ce genre de question, tu peux consulter la fiche suivante : Résoudre une inéquation polynomiale de degré 2 à une variable.
La quantité d'eau dans le réservoir d'une usine de traitement des eaux usées varie selon le moment de la journée. Cette situation peut être modélisée à l'aide d'une fonction polynomiale du second degré. Le réservoir de l'usine est rempli à pleine capacité, c'est-à-dire à 25 000 L, à midi. De plus, il est vide à 20 h.
a) Quelle est l'équation, sous la forme générale, associée à la quantité d'eau dans le réservoir selon le moment de la journée?
b) À quelles heures le réservoir de l'usine a-t-il une quantité de 15 000 L?
Il est très important de définir les variables :
|x:| moment de la journée (en heures);
|y:| quantité d'eau dans le réservoir.
Il est donc possible de trouver deux couples appartenant à la fonction, c'est-à-dire les couples |(12, 25\ 000)| et |(20,\ 0).|
Le couple |(12, 25\ 000)| correspond au maximum de la fonction.
a)
Pour trouver l'équation de la fonction modélisant cette situation, il faut utiliser la forme canonique. En effet, le point |(12, 25\ 000)| étant le sommet, c'est la forme canonique qui est de mise pour trouver l'équation.
La forme canonique de la fonction polynomiale du second degré est |y=a(x-h)^2+k.| Dans cette situation, |(h,k)=(12,25\ 000)| et |(x,y)=(20,0).| On remplace donc ces paramètres et ces variables dans l'équation : ||y=a(x-h)^2+k \rightarrow 0=a(20-12)^2+25\ 000||
On isole maintenant la valeur de |a.| || \begin{align}0&=a(20-12)^2 + 25\ 000 \\ 0&= a(8)^2 + 25\ 000 \\ 0&= 64a + 25\ 000 \\ -25\ 000 &= 64a \\ -390{,}625&= a \end{align}||
Ainsi, l'équation de la fonction sous la forme canonique est : ||y=-390{,}625(x-12)^2 + 25\ 000||
Il ne reste qu'à passer de la forme canonique à la forme générale en effectuant les manipulation algébriques. ||\begin{align}y&=-390{,}625(x-12)^2+25\ 000 \\ y&= -390{,}625(x-12)(x-12) +25\ 000 \\ y&= -390{,}625(x^2-24x+144) + 25\ 000 \\ y&= -390{,}625x^2 + 9\ 375x - 56\ 250 + 25\ 000 \\ y&= -390{,}625x^2 + 9\ 375x - 31\ 250 \end{align}||
Réponse : La forme générale est donc |y=-390{,}625x^2 + 9\ 375x - 31\ 250.|
b)
Pour déterminer à quelles heures le réservoir contient |15\ 000\ \text{L},| il faut substituer |y| par |15\ 000| dans l'équation. ||15\ 000=-390{,}625x^2+9\ 375x-31\ 250||
Pour résoudre une telle équation, il faut la rendre égale à 0. ||\begin{align} 15\ 000 &= -390{,}625x^2 + 9\ 375x - 31\ 250 \\ \Rightarrow \quad 0 &=-390{,}625x^2 + 9\ 375x-46\ 250 \end{align}||
Maintenant, afin de trouver les solutions de cette équation, il faut utiliser la formule quadratique : |\displaystyle x_{1,2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a}|
Dans ce cas, |a=-390{,}625, b=9\ 375| et |c=-46\ 250|. ||\begin{align}\displaystyle x_{1,2} &= \frac{-9\ 375 \pm \sqrt{9\ 375^2 - 4\times -390{,}625 \times -46\ 250}}{2 \times -390{,}625} \\ \displaystyle x_{1,2} &= \frac{-9\ 375 \pm \sqrt{15\ 625\ 000}}{-781{,}25}\end{align}||
On sépare la formule en deux parties. ||\begin{align}\displaystyle x_1 &= \frac{-9\ 375 + \sqrt{15\ 625\ 000}}{-781{,}25} \approx 6{,}94\\ \displaystyle x_2 &= \frac{-9\ 375 - \sqrt{15\ 625\ 000}}{-781{,}25} \approx 17{,}06 \end{align}||
Pour donner la réponse à la question, il faut transformer les deux valeurs |x_1| et |x_2| en heures et minutes :
-
|x_1| correspond à |6| heures et |56| minutes. En effet, |0{,}94 \times 60 = 56{,}4| minutes, qu'on peut arrondir à |56| minutes.
-
|x_2| correspond à |17| heures et |4| minutes. En effet, |0{,}06 \times 60 = 3{,}6| minutes, qu'on peut arrondir à |4| minutes.
Réponse : Le niveau du réservoir sera de 15 000 L à 6 h 56 et à 17 h 04.
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction polynomiale de degré 2 de façon interactive, consulte la MiniRécup suivante.
