Solving this kind of system is the same as finding the point or points of intersection between a parabola and a line. Make sure to first be comfortable with solving a second-degree equation.
Here is a table showing the number of possible solutions of such a system.
|
No solution |
One solution |
Two solutions |
|---|---|---|
 |
 |
 |
|
There is no intersection between the line and the parabola. |
The line is tangent to the curve of the parabola. |
The line intersects the parabola. |
Follow these steps to solve a system of equation of this type.
-
Make the two equations equal to each other using the comparison method.
If the equation of the parabola is not of the form |y=ax^2+bx+c|, convert the equation to this form. Also, if the equation of the linear function is not of the form |y=ax+b|, convert it to this form. -
Move all the terms to one side of the equation so that the other side is equal to |0|. Next, determine the number of solutions.
Using the new equation |ax^2+bx+c=0| and the value of |b^2-4ac,| it is possible to determine the number of solutions.
-
If |b^2-4ac<0,| there is no solution.
-
If |b^2-4ac=0,| there is only one solution.
-
If |b^2-4ac>0,| there are two solutions.
-
Factor (if possible) or use the quadratic formula to find the solution(s) in terms of |x.|
-
Find the solution(s) in terms of |y.|
-
Give the point(s) that serve as solutions.
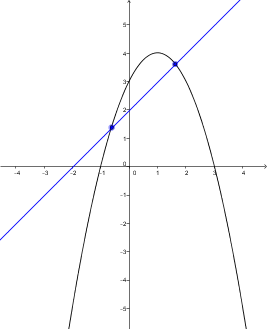
Consider the following system of equations. ||\begin{cases}y=-x^2+2x+5\\y=x+3\end{cases}||
-
Compare the two functions by writing the equation |-x^2+2x+5=x+3.|
-
Move all the terms to one side of the equation. In this case, send the terms to the left (or to the right, since both work). ||\begin{align}-x^2+2x+5 &= x+3 \\ \Rightarrow\ -x^2+x+2 &= 0 \end{align}|| |b^2-4ac=1^2-4(-1)(2) = 9 >0,| so the system of equations has two solutions.
-
Use the quadratic formula |x_{1,2} = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}| where |a=-1|, |b=1,| and |c=2.| ||\begin{align}x_{1,2} &= \dfrac{-1 \pm \sqrt{1^2 - 4 (-1)(2)}}{2 \times 1} \\ &= \dfrac{-1 \pm \sqrt{9}}{2} \\ &= \dfrac{-1 \pm 3}{2} \\\\ x_1&= \dfrac{-1 + 3}{-2} = -1 \\ x_2 &= \dfrac{-1-3}{-2} = 2 \end{align}||
-
Find the values of |y| by substituting in the values of |x| into either of the two initial equations. ||\begin{align}y_1 &= \ x_1+3 &y_2 &= x_2+3 \\ &= -1+3 & &=\ 2\ +3 \\ &=\ 2 & &=\ 5 \end{align}||
-
The points |(-1,2)| and |(2,5)| are the solutions.
Consider the following system of equations. ||\begin{cases}y=-2x^2+x-2 \\y=\ 2x+1 \end{cases}||
-
Write out the following equality: |-2x^2+x-2=2x+1.|
-
Move all the terms to one side of the equation. In this case, to the left side. ||\begin{align} -2x^2+x-2 &= 2x+1 \\ \Rightarrow\ -2x^2-x-3 &= 0 \end{align}||
|b^2-4ac = (-1)^2 - 4 (-2)(-3) = -23 <0,| so there is no solution to this system.
Therefore, there is no point of intersection and no solution exists.
Consider the following system of equations. ||\begin{cases}y=-2x^2+x-3 \\ y=-3x-1 \end{cases}||
-
Write the following equality: |-2x^2+x-3=-3x-1.|
-
Move all the terms to one side of the equation. In this case, to the left side. ||\begin{align} -2x^2+\ x-3 &= -3x-1 \\ \Rightarrow\ -2x^2+4x-2 &=0 \end{align}||
|b^2-4ac = 4^2 - 4(-2)(-2) = 0,| so there is only one solution to the system. -
Factor |-2x^2+4x-2| to transform the equation into |-2(x-1)^2.|
Next, solve |-2(x-1)^2=0.| ||\begin{align} -2(x-1)^2 &= 0 \\ (x-1)^2 &=0 \\ x-1&= 0 \\ \Rightarrow\ x &= 1 \end{align}|| -
Find the value of |y| by replacing |x| with |1.| ||\begin{align} y &=-3x-1 \\ &= -3(1) -1 \\ &= -4 \end{align}||
-
The solution is the point |(1,-4).|