Heron's formula is a formula which allows us to find the area of any triangle when the three side lengths are given.
If we know the measures |a|, |b|, and |c| of the three sides of any triangle ABC, we can calculate the area of the triangle using Heron's formula.
The area A of any triangle whose side lengths are |a,| |b|, and |c,| is determined by the following formula: ||A=\sqrt{p(p-a)(p-b)(p-c)}||
where |p| represents the half-perimeter of the triangle, determined by the following formula: ||p=\frac{a+b+c}{2}||
Let's calculate the area of the following triangle.
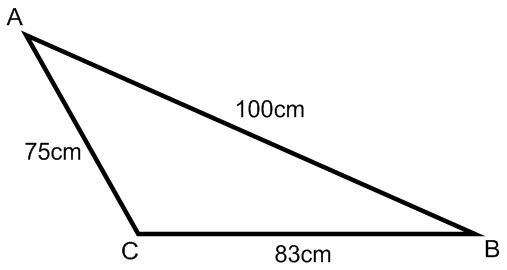
Calculation of the half-perimeter:
||\begin{align} p &=\frac{a+b+c}{2} \\\\
&=\frac{75+83+100}{2}\\\\
&=129\ \mathrm{cm}\\\\
\Rightarrow A&=\sqrt{p(p-a)(p-b)(p-c)}\\
&=\sqrt{129(129-75)(129-83)(129-100)}\\
&=3\ 048{.}38\ \mathrm{cm}^{2}\end{align}||
The area of triangle ABC is |3\ 048{.}38\ \mathrm{cm}^2|.
Find the area of the following triangle:
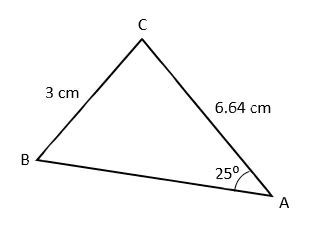
First, determine the missing length for the third side of the triangle. To do this, use sine law.
||\begin{align} \frac{a}{\sin A} &= \frac{b}{\sin B} &&= \frac{c}{\sin C}\\\\
\Rightarrow \frac{3}{\sin 25°} &= \frac{6{.}64}{\sin B} &&\\\\
\frac{6{.}64\times {\sin 25°}}{3} &= \sin B &&\\\\
0{.}9354 &\approx \sin B &&\\
69{.}29^\circ &\approx B && \end{align}||
The third angle (angle C) is therefore:
||180 - 25 - 69{.}29 = 85{.}71°||
Therefore, we can use sine law again to determine the measure of the missing side.
||\begin{align} \frac{3}{\sin 25°} &= \frac{c}{\sin 85{.}71°}\\\\
\frac{\sin 85{.}71° \times {3}}{\sin 25°} &= c\\\\
7{.}08 &\approx c\end{align}||
Now that we know the measure of the missing side, we can calculate the half-perimeter and find the area of the triangle using Heron’s formula.
||\begin{align} p&=\frac{a+b+c}{2}\\\\
&=\frac{3 + 6{.}64 + 7{.}08}{2}\\\\
&=8{.}36\ \mathrm{cm} \\\\
\Rightarrow A&=\sqrt{p(p-a)(p-b)(p-c)}\\
&=\sqrt{8{.}36(8{.}36-3)(8{.}36-6{.}64)(8{.}36-7{.}08)}\\
&=10\ \mathrm{ cm}^{2}\end{align}||
The area of the triangle is |10\ \mathrm{ cm}^2.|
Trigonometric formula
It is also possible to calculate the area of a triangle if we know the measure of two of its sides and the measure of the angle between those sides. We then use the following trigonometric formula: ||A = \frac{a\times b \times \sin C}{2}||
To confirm you understand Héron's formula, see the interactive CrashLesson on trigonometry:
