The chromatic number of a graph is the minimum number of colours that must be used to colour all the vertices of a graph, making sure that two adjacent vertices are not the same colour.
Coloured graphs and chromatic numbers are used to solve planning problems when certain incompatibilities must be taken into account.
The following situations are examples of where it can be useful to find the chromatic number: scheduling, classifying species of animals or plants, colouring countries on a world map, etc.
Steps to solve a problem using a chromatic number:
-
Draw a graph that represents the situation where the vertices are the different elements and the edges illustrate the incompatibilities between those elements.
-
List the vertices of the graph in decreasing order of degree (the order does not matter for two vertices that have the same degree).
-
Colour the first vertex of the list (the one with the highest degree) with any colour.
-
Moving down the list, assign the same colour to the other vertices that are not connected to the first vertex or to each other.
-
Repeat steps 3 and 4 with a new colour each time until the vertices are all coloured.
-
Count the number of colours used, which is the chromatic number, and answer the question.
The organizers of a music festival must plan the performance schedule for the different groups on the programme, but they have several constraints that must be respected.
-
The Amateurs cannot play at the same time as The Good-For-Nothings because both groups have the same drummer.
-
The singer Calvin Harry cannot perform at the same time as Dany Lavoto since both use the same stage equipment.
-
Calvin Harry and Janis Jackson do not want to perform on stage at the same time since they share the same audience.
-
The following artists: Calvin Harry, Janis Jackson, Eleanor Rugby, and Dany Lavoto refuse to do their show at the same time as The Brave Penguins because they are too popular and would result in not enough spectators for their own shows.
-
Finally, Janis Jackson does not want to play at the same time as The Good-For-Nothings because she absolutely wants to attend their show.
In light of all these constraints, what is the minimum number of stages and evening spots that will be necessary to present all these shows during this festival?
-
Draw the graph representing the situation where the vertices are the different elements and the edges illustrate the incompatibilities between the elements
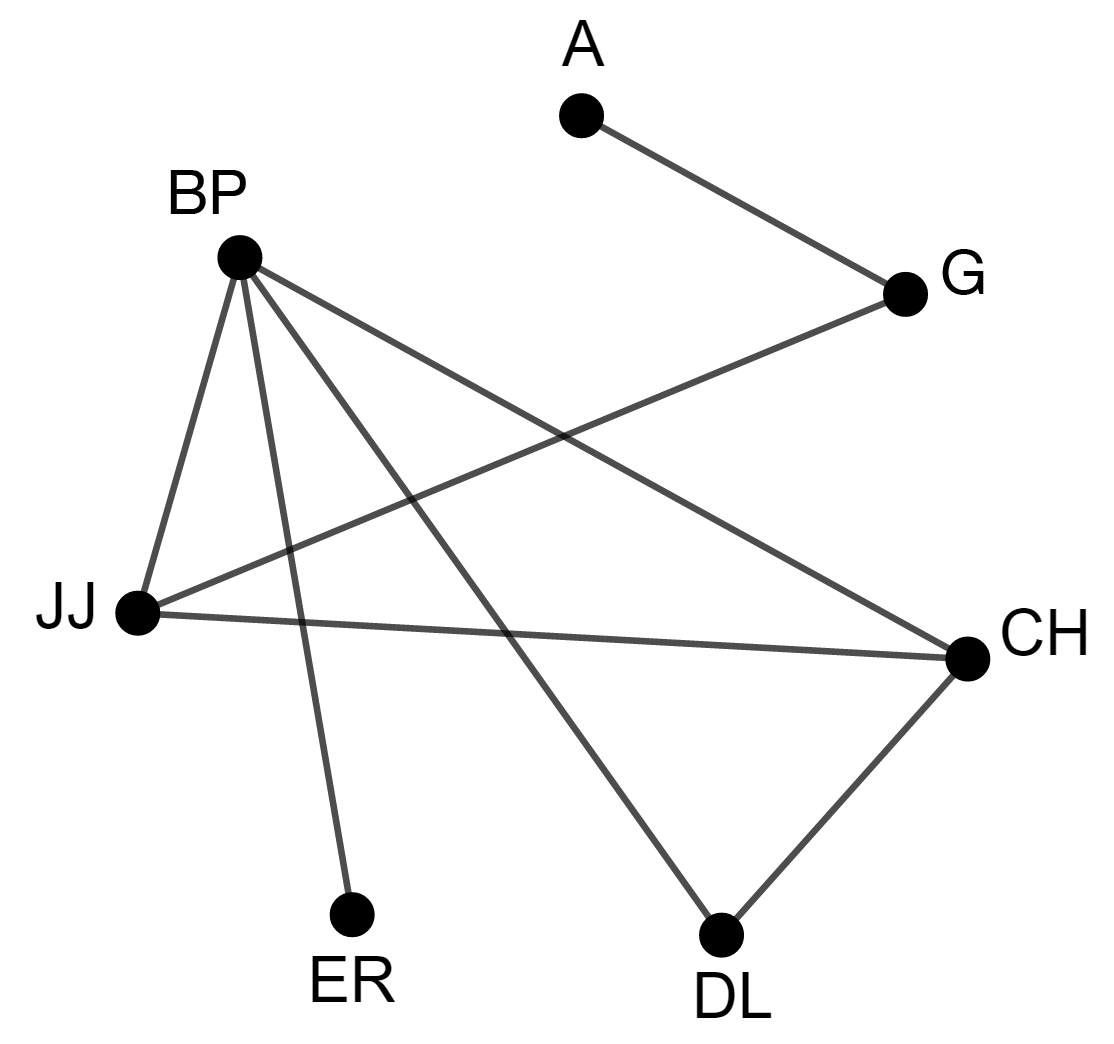
|
Legend |
|---|
|
A: The Amateurs |
-
List the vertices of the graph in decreasing order of degree
BP (4), CH (3), JJ (3), DL (2), G (2), A (1), ER (1) -
Colour the first vertex of the list with any colour
The vertex BP is the vertex with the greatest degree, 4. It is coloured blue. -
Moving down the list, assign the same colour to the other vertices that are not connected to the first vertex nor to each other
The only vertices which are not connected to BP and which are connected to each other are A and G. Then colour G, since it is the next on the list. -
Repeat steps 3 and 4 with a new colour each time until the vertices are all coloured
The next highest degree vertices are CH and JJ. Choose CH and colour it green. It is also possible to assign the colour green to the vertices A and ER, which are not connected to each other nor to CH.
Finally, the last 2 vertices which remain to be coloured are not connected to each other. They can therefore be assigned the same colour without problem. Here, the colour red is chosen.
Here is the graph representing the situation.
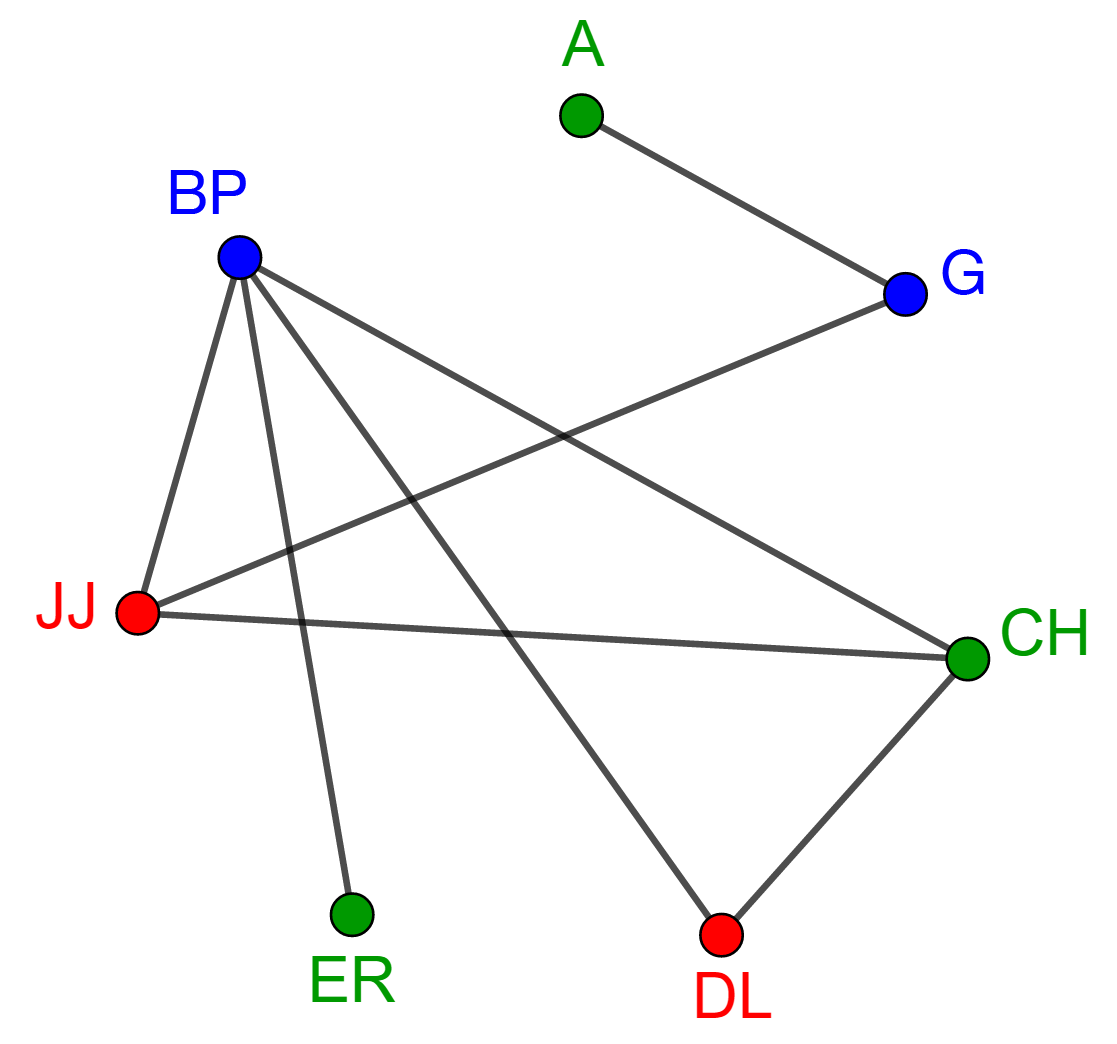
|
Legend |
|---|
|
A: The Amateurs |
-
Calculate the number of colours used, which is the chromatic number, and answer the question
3 different colours have been used, so the chromatic number of this graph is therefore 3. But what does this mean for this situation?
The groups that have been coloured the same colour will be able to perform their shows on the same evening. Since the chromatic number is 3, this means that it will take 3 evenings to perform each show. Since there are 3 green vertices (and only 2 in blue and 2 in red), this means that it will take 3 stages to simultaneously perform the shows of The Amateurs, Calvin Harry, and Eleanor Rugby.
Note: At step 5, if we had chosen vertex JJ instead of vertex CH, we would have gotten the same number of evenings, but a different number of stages.