When several geometric transformations are completed successively, the rule that connects these transformations is a composition and the result is called the composite. We use the symbol |\circ| that is read as "composite".
The transformations of a composition are always completed from right to left.
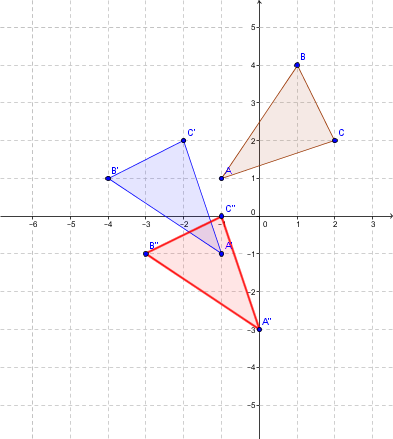
Consider the triangle |ABC|. We want to complete the transformation |t_{(1,-2)} \circ r_{(O,90°)}.|
At the start, complete a centre rotation |O| (here, it is the origin of the Cartesian plane) followed by a translation.
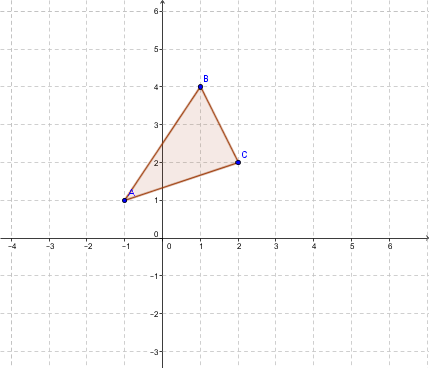
The coordinates of the vertices of the triangle |ABC| are:
-
|A(-1,1)|;
-
|B(1,4)|;
-
|C(2,2)|.
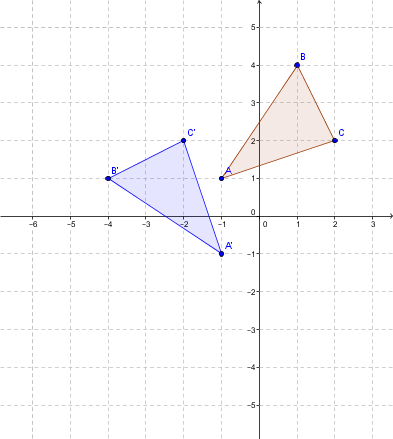
Step 1: Complete the rotation with centre |O| and angle |90°| in a counterclockwise direction
Use the following rule |r_{(O,90°)}:(x,y) \mapsto (-y,x)|.
|A=(-1,1) \mapsto (-1,-1)=A'|;
|B=(1,4) \mapsto (-4,1)=B'|;
|C=(2,2 \mapsto (-2,2)=C'|.
The blue triangle is obtained.
Step 2: Complete the translation with the rule |t_{(1,-2)}:(x,y) \mapsto (x+1,y-2)|
After completing it, the following points are obtained.
-
|A'=(-1,-1) \mapsto (0,-3)=A''|;
-
|B'=(-4,1) \mapsto (-3,-1)=B''|;
-
|C'=(-2,2) \mapsto (-1,0)=C''|.
This gives the red triangle which is the image figure.