Geometric transformations make it possible to associate any initial figure with an image figure (final figure).
There are four main geometric transformations:
-
Translation
-
Rotation
-
Reflection
-
Dilation
A geometric transformation that does not change the measurements of a figure is an isometry. Translations, rotations, and reflections are all isometries.
A geometric transformation associating similar figures is called a similitude. Dilation is a similitude.
When several geometric transformations are performed successively, the rule connecting the transformations is a composition and the result is called the composite. The symbol |\circ| is used, which means "composite".
The composition |t_{(a,b)} \circ s_x| corresponds to the reflection of a figure in relation to the axis of |x| followed by a translation. We read the composition as “|t| composite |s_x|“.
Note:
-
We perform the transformations from right to left.
-
A reflection followed by a translation (in the same direction as the axis of reflection) is an isometry called a glide reflection.
See the following concept sheets to learn how to perform various geometric transformations in a Cartesian plane:
Recognizing transformations requires mastering the rules and associating them with the correct transformations.
|
Rules |
Transformations |
Remarks |
|
|(x,y) \mapsto (x+a,y+b)| |
Translation of |a| units horizontally and |b| units vertically. |
It is the only transformation involving |+| and |-|. |
|
|(x , y) \mapsto (-y, x)| |
Rotation of |90°| or |-270°| centered at the origin. |
The order of the letters has been changed and the first coordinate becomes negative. |
|
|(x , y) \mapsto (-x, -y)| |
Rotation of |180°| or |-180°| centered at the origin. |
Since the figure makes a u-turn, we only change the signs. |
|
|(x , y) \mapsto (y, -x)| |
Rotation of |270°| or |-90°| centered at the origin. |
The order of the letters has been changed and the second coordinate becomes negative |
|
|(x,y) \mapsto (x,-y)| |
Reflection with respect to the |x|-axis. |
Only the |y| changes sign. |
|
|(x , y) \mapsto (-x, y)| |
Symétrie par rapport à l’axe des |y| |
Only the |x| changes sign. |
|
|(x , y) \mapsto ( y, x)| |
Symmetry with respect to the bisector of quadrants |1| and |3|. |
We change the order of the letters. |
|
|(x , y) \mapsto (-y, -x)| |
Symmetry with respect to the bisector of quadrants |2| and |4|. |
We change both the order and the signs. |
|
|(x, y) \mapsto (kx, ky)| |
Dilation Ratio |k| |
It is the only transformation which involves multiplication by coefficients different from |1|. |
Compare the coordinates of the corresponding vertices to find the transformation which links two figures in a Cartesian plane, i.e., the |A| with the |A’|, the |B| with the |B’|, etc.
Translation example
We translate the pink triangle and obtain the blue triangle.
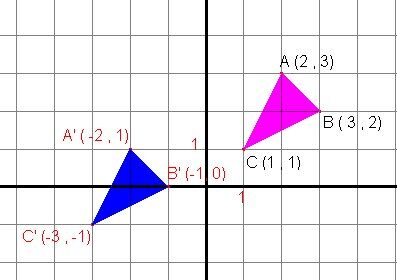
We compare the coordinates of the corresponding vertices:
|A| and |A’|: |(2,3)| and |(-2,1)|;
|B| and |B’|: |(3,2)| and |(-1,0)|;
|C| and |C’|: |(1,1)| and |( -3,-1)|.
There is no multiplication of the coordinates, no change of order, and no significant change of sign. Only the translation remains as an admissible transformation.
We locate the rule:
The value in |x| of point |A| went from |2| to |-2|, i.e., a difference of |4|.
The value in |x| of point |B| went from |3| to |-1|, i.e., a difference of |4|.
The value in |x| of point |C| went from |1| to |-3|, i.e., a difference of |4|.
The value in |y| of point |A| went from |3| to |1|, i.e., a difference of |2|.
The value in |y| of point |B| went from |2| to |0|, i.e., a difference of |2|.
The value in |y| of point |C| went from |1| to |-1|, i.e., a difference of |2|.
Therefore, the rule of translation is: |t_{(-4,-2)}: (x,y) \mapsto (x – 4,y – 2)|.