The law of cosines is a formula used to find the measurement of a side or an angle of a triangle. It works on all triangles.
The law of cosines is a generalization of the Pythagoras Theorem for triangles. It enables us to find the measurement of any triangle’s side or angle. To use this formula, the measurements of two sides and the angle they form, or the measurements of all three sides, must be known.
The law of cosines can appear as:
||\begin{align} a^2 &= b^2 + c^2 – 2bc\cos A\\
b^2 &= a^2 + c^2 – 2ac\cos B\\
c^2 &= a^2 + b^2 – 2ab\cos C\end{align}||
with
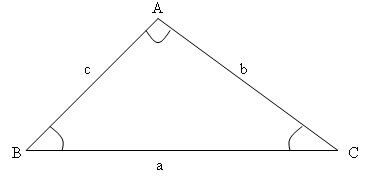
In general, the law of cosines is used in two situations:
-
When the measurements of two sides and the angle they form are known, it allows us to find the measurement of the third side (as in the triangle below on the left).
-
When the measurements of three sides of a triangle are known, it allows us to find the measurement of an angle (as in the triangle below on the right).
What is the measurement of the side |\overline{AB}| in the triangle below?
||\begin{align} c^2 &= a^2 + b^2 – 2ab\cos C\\
&= 10^2 + 8^2 – 2(10)(8)\cos 70^\circ\\
&= 100 + 64 - 160\cos 70^\circ\\
&= 164 - 160\cos 70^\circ\\
&\approx 164 - 54{.}72\\
&\approx 109{.}28\\
c &\approx 10{.}45\end{align}||
Answer: The side |\overline{AB}| measures approximately |10{.}45| cm.
What is the measurement of angle |R| in the triangle below?
||\begin{align}
r^2&=s^2+t^2-2st\cos R\\
4^2&=7^2+6^2-2(7)(6)\cos R\\
16&=49+36-84\cos R\\
16&=85-84\cos R\\
-69&=-84\cos R\\
0{,}821&\approx\cos R\\
m\angle R&\approx\cos^{-1}(0{.}821)\\
m\angle R&\approx34{.}77^\circ
\end{align}||
Answer: Angle |R| measures approximately |34{.}77| degrees.
What is the measurement of the third side of the triangle below?
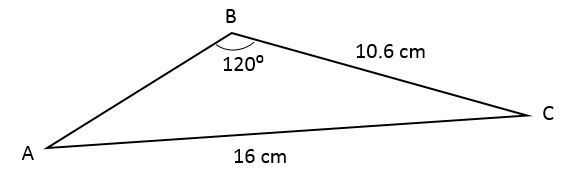
In the following example, it may be helpful to use the law of cosines. First, we propose the equation relating to the measurement of the third side and the known measurements:
||b^2 = a^2 + c^2 – 2ac\cos B||
where:
||\begin{align} a& =10{.}6\ \mathrm{cm} \\
b &=16\ \mathrm{cm} \\
c &= \ \text{measurement of third side} \\
m\angle B &=120°\end{align}||
Using the formula, as follows:
||\begin{align} 16^2 &= 10{.}6^2 + c^2 - 2(10{.}6)(c)\cos 120° \\
256 &= 112{.}36 + c^2 - 21{.}2(c)(-0,5) \\
256 &= 112{.}36 + c^2 + 10{.}6c \\
0 &= 112{.}36 - 256 + c^2 + 10{.}6c \\
0 &= c^2 + 10{.}6c - 143{.}64\\\\
\Rightarrow c &= \frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\\\
&= \frac{-10{.}6\pm\sqrt{10{.}6^{2}-4\times 1\times-143{.}64}}{2\times 1}\\\\
&= \frac{-10{.}6\pm\sqrt{686{.}92}}{2} \\\\
&\approx \frac{-10{.}6\pm26{.}21}{2}\\\\
&\approx 7{.}80 \ \text{or} \ \text{-}18{.}40\end{align}||
The negative value is rejected, since we are looking for a side measurement.
Answer: The side |\overline{AB}| measures approximately |7{.}80| cm.
To confirm your understanding of the trigonometry, see the following interactive CrashLesson:
