La loi des cosinus

​​​​La loi des cosinus est une formule qui permet de trouver la mesure d'un côté ou d'un angle dans un triangle quelconque. Elle est donc valable pour tous les triangles.

La loi des cosinus peut prendre les formes suivantes :

||\begin{align} a^2 &= b^2 + c^2 – 2bc\cos A\\
b^2 &= a^2 + c^2 – 2ac\cos B\\
c^2 &= a^2 + b^2 – 2ab\cos C\end{align}||

avec

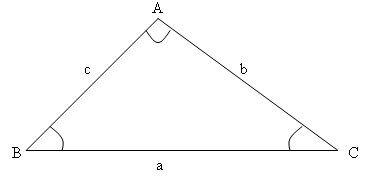
Généralement, on utilise la loi des cosinus dans deux situations :

• lorsqu'on connait les mesures de deux côtés et de l'angle qu'ils forment dans le triangle ce qui permet de trouver la mesure du troisième côté (comme dans le triangle de gauche ci-dessous);

• lorsqu'on connait les mesures des trois côtés du triangle ce qui permet de trouver la mesure d'un angle (comme dans le triangle de droite ci-dessous).

Quelle est la mesure du côté |\overline{AB}| dans le triangle ci-dessous?

||\begin{align} c^2 &= a^2 + b^2 – 2ab\cos C\\
 &= 10^2 + 8^2 – 2(10)(8)\cos 70^\circ\\
 &= 100 + 64 - 160\cos 70^\circ\\
 &= 164 - 160\cos 70^\circ\\
 &\approx 164 - 54{,}72\\
 &\approx 109{,}28\\
c &\approx 10{,}45\end{align}||

Réponse : Le côté |\overline{AB}| mesure environ |10{,}45| cm.

Quelle est la mesure de l'angle |R| dans le triangle ci-dessous?

||\begin{align}
r^2&=s^2+t^2-2st\cos R\\
4^2&=7^2+6^2-2(7)(6)\cos R\\
16&=49+36-84\cos R\\
16&=85-84\cos R\\
-69&=-84\cos R\\
0{,}821&\approx\cos R\\
m\angle R&\approx\cos^{​-1}(0{,}821)\\
m\angle R&\approx34{,}77^\circ
\end{align}||

Réponse : L'angle |R| mesure environ |34{,}77| degrés.

​Quelle est la mesure du troisième côté du triangle ci-dessous?

Dans cet exemple, il peut être utile de se servir de la loi des cosinus. On pose d’abord l’équation mettant en relation la mesure du troisième côté et les mesures connues :

||b^2 = a^2 + c^2 – 2ac\cos B||

dans laquelle :

||\begin{align} a& =10{,}6\ \mathrm{cm} \\
b &=16\ \mathrm{cm} \\
 c &= \ \text{mesure du troisième côté} \\
m\angle B &=120°\end{align}||

En utilisant la formule, on obtient,
||\begin{align} 16^2 &= 10{,}6^2 + c^2 - 2(10{,}6)(c)\cos 120° \\
256 &= 112{,}36 + c^2 - 21{,}2(c)(-0,5) \\
256 &= 112{,}36 + c^2 + 10{,}6c \\
0 &= 112{,}36 - 256 + c^2 + 10{,}6c \\
0 &= c^2 + 10{,}6c - 143{,}64\\\\
\Rightarrow c &= \frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\\\
&= \frac{-10{,}6\pm\sqrt{10{,}6^{2}-4\times 1\times-143{,}64}}{2\times 1}\\\\
&= \frac{-10{,}6\pm\sqrt{686{,}92}}{2} \\\\
&\approx \frac{-10{,}6\pm26{,}21}{2}\\\\
&\approx 7{,}80 \ \text{ou} \ \text{-}18{,}40\end{align}||

La valeur négative est à rejeter puisqu'on cherche une mesure de côté.

Réponse : Le côté |\overline{AB}| mesure environ |7{,}80| cm.