Operations on functions are performed in the same way as operations on numbers are performed.
Given two real functions |f| and |g,| the product of them is defined as:
||(f \times g)(x)=f(x)\times g(x)||
The domain of the product of functions corresponds to the intersection of the domains of the functions in question. If there is a denominator, the restrictions on it must be excluded from the final domain.
The symbol sometimes used for multiplication should not be confused with the symbol for the composition of functions.
-
Multiplication: |\cdot|
-
Composition: |\circ|
Function |s| is defined by |s(x)=\dfrac{1}{(x^{2}-1)}| and function |t| is defined by |t(x)=x^{2}-x.| Multiplying the functions will result in: ||\begin{align}(s\times t)(x) &= s(x)\times t(x) \\ &=\dfrac{1}{(x^{2}-1)}\times (x^{2}-x) \\ &=\dfrac{1}{(x+1)(x-1)}\times (x)(x-1) \\ &= \dfrac{(x)\cancel{(x-1)}}{(x+1)\cancel{(x-1)}} \\ &= \dfrac{x}{x+1} \\ &=\frac{-1}{x+1}+1 \end{align}||
The domain of function |s| corresponds to |\mathbb{R}\backslash \lbrace -1,1 \rbrace| and the domain of function |t| corresponds to |\mathbb{R}.| The domain of the function given by |s\times t| will correspond to the intersection of the two initial domains. Next, we add the restriction to the denominator before the simplification |x \neq \lbrace -1, 1 \rbrace.| The result is |\mathbb{R} \backslash \lbrace -1,1 \rbrace.|
Function |u| is defined by |u(x)=\dfrac{2x^{2}-1}{x+3}| and function |v| is defined by |v(x)=-1.| ||\begin{align} (u\times v)(x) &= u(x)\times v(x) \\ &=\dfrac{2x^{2}-1}{x+3}\times -1 \\ &=\frac{-2x^{2}+1}{x+3} \end{align}||
The domain of function |u| corresponds to |\mathbb{R} \backslash \lbrace -3 \rbrace| and the domain of function |v| corresponds to |\mathbb{R}|. The domain of the function given by |u\times v| will correspond to the intersection of the two initial domains, to which we must add the restriction to the denominator |x \neq -3.| Therefore, this function’s domain will be |\mathbb{R} \backslash \lbrace -3 \rbrace.|
To find the product of functions in a graph, multiply the range of the first function by the range of the second function.
To produce the graph, create a table of values or use the peculiarities of the resulting function.
In the first example, a table of values of the functions |s(x)=\dfrac{1}{(x^{2}-1)},| |t(x)=x^{2}-x| and |(s\times t)(x)=\dfrac{x}{x+1},| will result in:
| |x| | |s(x)| | |t(x)| | |(s\times t)(x)| |
|---|---|---|---|
| |0| | |-1| | |0| | |0| |
| |1| |
undefined |
|0| |
undefined |
| |2| | |\dfrac{1}{3}| | |2| | |\dfrac{2}{3}| |
|
|3| |
|\dfrac{1}{8}| | |6| | |\dfrac{3}{4}| |
| |4| | |\dfrac{1}{15}| | |12| | |\dfrac{4}{5}| |
Since the resultant is a rational function, its peculiarities can be used to plot the equation.
||(s\times t)(x)=\dfrac{-1}{(x+1)}+1||
-
There are two asymptotes: |x=-1| et |y =1.|
-
Since |ab<0,| the function is located in the 2nd and 4th quadrant. The result is the following graph:
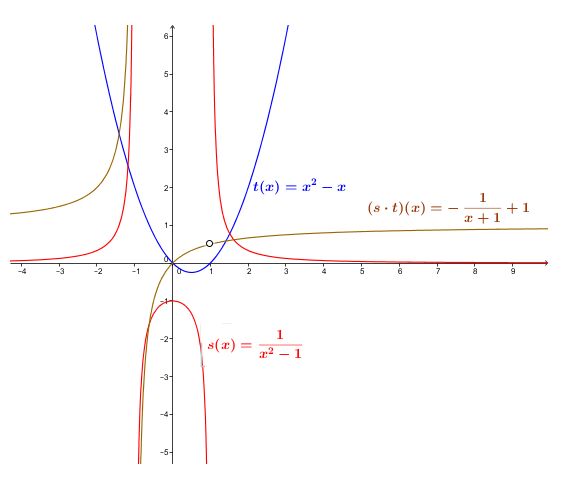
Do not forget the restriction of |x=1.| The other restriction corresponds to the asymptote of equation |x=-1.|
Pour valider ta compréhension des opérations sur les fonctions de façon interactive, consulte la MiniRécup suivante :
