On effectue des opérations sur les fonctions de la même manière que l’on effectue des opérations sur les nombres.
Étant donné deux fonctions réelles |f| et |g,| on définit le produit de celles-ci comme suit :||(f \times g)(x)=f(x)\times g(x)||
Le domaine de la fonction produit correspond à l’intersection des domaines des fonctions sur lesquelles on opère. S'il y a un dénominateur, il faut exclure du domaine final les restrictions sur ce dernier.
Il ne faut pas confondre le symbole parfois utilisé pour la multiplication avec le symbole de la composition de fonctions.
-
multiplication : |\cdot|
-
composition : |\circ|
La fonction |s| est définie par |s(x)=\dfrac{1}{(x^{2}-1)}| et la fonction |t| est définie par |t(x)=x^{2}-x|. La multiplication de ces fonctions donnera le résultat suivant : ||\begin{align}(s\times t)(x) &= s(x)\times t(x) \\ &=\dfrac{1}{(x^{2}-1)}\times (x^{2}-x) \\ &=\dfrac{1}{(x+1)(x-1)}\times (x)(x-1) \\ &= \dfrac{(x)\cancel{(x-1)}}{(x+1)\cancel{(x-1)}} \\ &= \dfrac{x}{x+1} \\ &=\frac{-1}{x+1}+1 \end{align}||
Le domaine de la fonction |s| correspond à |\mathbb{R}\backslash \lbrace -1,1 \rbrace| et le domaine de la fonction |t| correspond à |\mathbb{R}|. Le domaine de la fonction |s\times t| correspondra à l’intersection des deux domaines initiaux auquel on doit ajouter la restriction au dénominateur avant la simplification |x \neq \lbrace -1, 1 \rbrace|. On obtient alors |\mathbb{R} \backslash \lbrace -1,1 \rbrace|.
La fonction |u| est définie par |u(x)=\dfrac{2x^{2}-1}{x+3}| et la fonction |v| est définie par |v(x)=-1.| ||\begin{align} (u\times v)(x) &= u(x)\times v(x) \\ &=\dfrac{2x^{2}-1}{x+3}\times -1 \\ &=\frac{-2x^{2}+1}{x+3} \end{align}||
Le domaine de la fonction |u| correspond à |\mathbb{R} \backslash \lbrace -3 \rbrace| et le domaine de la fonction |v| correspond à |\mathbb{R}|. Le domaine de la fonction |u\times v| correspondra à l’intersection des deux domaines initiaux auquel on doit ajouter la restriction au dénominateur |x \neq -3.| Le domaine de la fonction sera donc |\mathbb{R} \backslash \lbrace -3 \rbrace.|
Pour trouver le produit de fonctions dans un graphique, on multiplie l’image de la première fonction par l'image de la deuxième fonction.
Pour être en mesure de produire le graphique, on peut faire une table des valeurs ou on peut utiliser les particularités de la fonction résultante.
Dans le premier exemple, si on fait une table des valeurs des fonctions |s(x)=\dfrac{1}{(x^{2}-1)},| |t(x)=x^{2}-x| et |(s\times t)(x)=\dfrac{x}{x+1},| on obtient :
| |x| | |s(x)| | |t(x)| | |(s\times t)(x)| |
|---|---|---|---|
| |0| | |-1| | |0| | |0| |
| |1| | non défini | |0| | non défini |
| |2| | |\dfrac{1}{3}| | |2| | |\dfrac{2}{3}| |
|
|3| |
|\dfrac{1}{8}| | |6| | |\dfrac{3}{4}| |
| |4| | |\dfrac{1}{15}| | |12| | |\dfrac{4}{5}| |
Puisque la résultante est une fonction rationnelle, on peut utiliser ses particularités pour tracer l'équation.
||(s\times t)(x)=\dfrac{-1}{(x+1)}+1||
-
On a deux asymptotes : |x=-1| et |y =1.|
-
Puisque |ab<0,| la fonction se retrouve dans le 2e et le 4e quadrant. On obtient le graphique suivant :
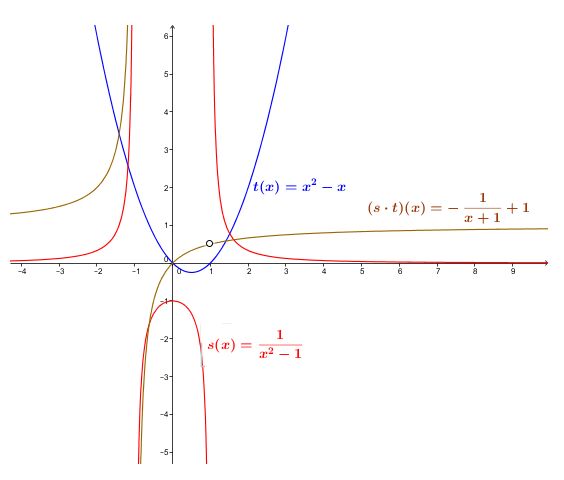
Il ne faut pas oublier la restriction en |x=1|. L'autre restriction correspond à l'asymptote d'équation |x=-1.|
Pour valider ta compréhension des opérations sur les fonctions de façon interactive, consulte la MiniRécup suivante :
