In the following animation, experiment with the values of parameters |a| and |b| of the first-degree polynomial function (linear function) and observe the effect on the function’s properties.
|
Properties |
Linear function of the form |y=ax+b| |
|---|---|
|
Domain |
|\mathbb{R}| or depending on the context |
|
Range (codomain) |
|\mathbb{R}| or depending on the context |
|
|x|-intercept |
|\displaystyle x = \frac{-b}{a}| or replace |y| with |0|, and then isolate |x| |
|
Sign of the function |
If |a>0| , the function is negative over |(-∞,\frac{-b}{a}]| and positive over |[\frac{-b}{a},+∞).| If |a<0| , the function is positive over |(-∞,\frac{-b}{a}]| and negative over |[\frac{-b}{a},+∞).| |
|
|y|-intercept |
The value of |b|. |
|
Extrema |
None, or depending on the context. |
|
Increasing intervals |
If the slope is positive |(a>0),| the function is increasing over its entire domain. |
|
Decreasing intervals |
If the slope is negative |(a<0),| the function is decreasing over its entire domain. |
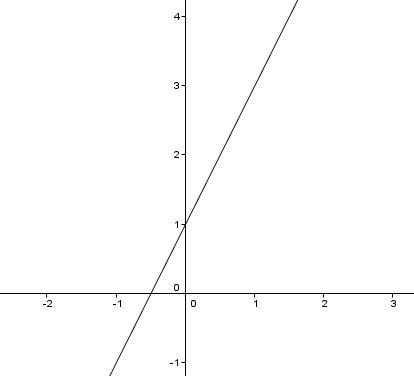
Determine the various properties of the function |y = 2x + 1|.
It is very useful to draw a graph to help determine the properties.
-
The domain of the function is the set of real numbers, denoted |\mathbb{R}|, since the function has no restrictions on its domain.
-
The range of the function is the set of real numbers, denoted |\mathbb{R}|, since the function outputs every real number.
-
The |x|-intercept of the function is calculated as follows: |\displaystyle x = \frac{-b}{a} = \frac{-1}{2}|. It is possible to replace |y| with |0|, and then isolate |x|.
||\begin{align} 0 &= 2x + 1 \\ -1 &= 2x \\ \displaystyle \frac{-1}{2} &= x \end{align}|| -
The sign of the function is negative over |(-∞,\frac{-1}{2}]| and positive over |[\frac{-1}{2},+∞).|
-
The |y|-intercept is |b = 1.|
-
The function has no extrema.
-
The function is increasing, because |a>0.|
Pour valider ta compréhension des propriétés des fonctions de façon interactive, consulte la MiniRécup suivante :
