In the following animation, select a sinusoidal function (sine or cosine), and then experiment with its parameters |a,| |b,| |h,| and |k|. Observe their effects on the function’s properties. After experimenting, read the concept sheet to understand the details of the properties of these functions.
The following table provides an analysis of the properties of the cosine function and shows examples.
|
Properties |
Standard Equation |
Example |
|---|---|---|
|
Formula |
|f(x)=a\cos\big(b(x-h)\big)+k| |
|f(x)=4\cos\big(2(x-\frac{5\pi}{4})\big)+3| |
|
Midline |
|y=k| |
|y=3| |
|
Period |
|P=\dfrac{2 \pi}{\mid b \mid }| |
|P=\dfrac{2\pi}{\mid 2 \mid}=\pi| |
|
Domain |
|\text{dom }f=\mathbb{R}| |
|\text{dom } f=\mathbb{R}| |
|
Range |
|\text{ran } f = [k-\mid a \mid ,\ k+\mid a \mid]| |
|[-1,7]| |
|
Variation |
|
Since |a| is positive, the function decreases from the point The function increases over the interval ||\left[\dfrac{3\pi}{4}+n\pi,\ \dfrac{5\pi}{4}+n\pi\right]|| The function decreases over the interval ||\left[\dfrac{5\pi}{4}+n\pi,\ \dfrac{7\pi}{4}+n\pi\right]|| |
|
Zeros of the Function |
These are the values of |x| for which |f(x)=0.| |x=x_{1}+nP| and |x=x_{2}+nP| where |P| is the period and |n\in \mathbb{Z}| |
|x=5{.}13+n\pi| |
|
y-intercept |
The value of |f(0)|. |
|f(0)=3| |
|
Sign |
The intervals where the function is positive and where the function is negative depend on the function’s zeros, the period, and the shape of the graph. |
The function is negative on the interval |[5{.}13+n\pi,\ 5{.}85+n\pi]| where |n\in\mathbb{Z}.| The function is positive on the interval |[5{.}85+n\pi,\ 8{.}28+n\pi]| where |n\in\mathbb{Z}.| |
|
Extrema |
Maximum : |k\ + \mid a\ \mid| |
Maximum : |7| |
Determine the following cosine function’s properties: ||f(x)=2\cos\left( \frac{3\pi}{4}(x-1)\right)+5|| It may be useful to plot a graph of the function.
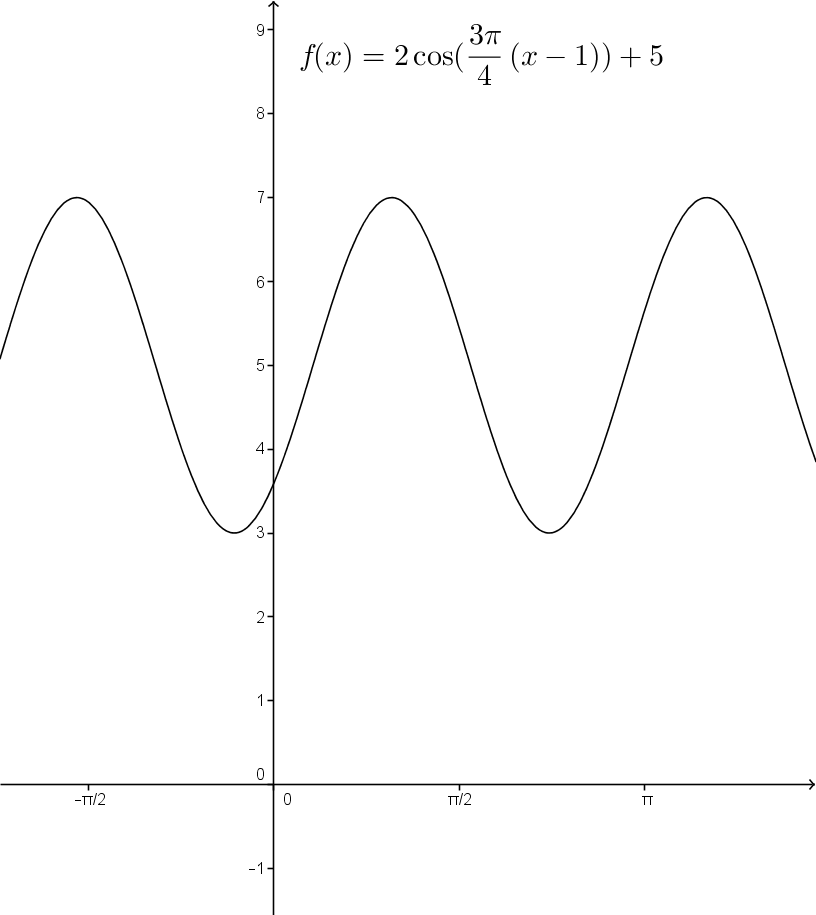
-
The equation of the midline of the function is |y=5.|
-
The parameter |b| is |\dfrac{3\pi}{4}| and the period of the function is |\displaystyle P = \frac{2\pi}{\mid b \mid} = \frac{2\pi}{\mid \frac{3\pi}{4} \mid } = \frac{8}{3}.|
-
The domain of the function is the set of real numbers, i.e. |\mathbb{R}.|
-
The range of the function is the interval |[k\ - \mid a \mid,\ k\ + \mid a \mid].| Here, |a=2| and |k=5.| Therefore, the range is |[3,\ 7].|
-
The variation: the parameter |a| is positive, so the function decreases after the point |(h,\ k\ + \mid a \mid),| i.e. after the point |(1,7).|
-
In general, the function decreases over the intervals|\left[1 + \dfrac{8n}{3}, \dfrac{7}{3} + \dfrac{8n}{3}\right]| where |n \in \mathbb{Z}.|
-
It increases over the intervals |\left[\dfrac{7}{3} + \dfrac{8n}{3}, \dfrac{11}{3} + \dfrac{8n}{3}\right]| where |n \in \mathbb{Z}.|
-
-
The function has no zero. Since the axis of oscillation is equal to 5 and the amplitude is equal to 2, the minimum of the function is 3. This can also be seen by performing calculations. Replace |f(x)| by |0.|
||\begin{align}0 &= 2\cos\left(\frac{3\pi}{4}(x-1)\right)+5\\-5 &= 2 \cos\left(\frac{3 \pi}{4}(x-1)\right)\\-2{.}5 &= \cos\left(\frac{3 \pi}{4}(x-1)\right)\end{align}||
At this stage everything stops. The values of the cosine are between -1 and 1. Therefore, the cosine can never be equal to |-2{.}5.|
-
The y-intercept is calculated by replacing |x| by |0.|
||\begin{align} f(0) &= 2\cos\left(\frac{3\pi}{4}(0-1)\right)+5\\f(0) &= 2\cos\left(-\frac{3\pi}{4}\right) + 5 \\ (\text{} &\text{consult the unit circle})\\ f(0) &= 2 \times -\frac{\sqrt{2}}{2} + 5 \\ f(0) &= -\sqrt{2} +5\approx 3{.}59 \end{align}||
-
The sign or positive and negative intervals of the function: as the function has no zero, it is positive over the whole of its domain.
-
The extrema of the function are:
-
Maximum : |k\ + \mid a \mid\, = 5+2 = 7|
-
Minimum : |k\ - \mid a \mid\, =5-2 = 3|
-
Both sine and cosine functions are sinusoidal functions. The same curve can therefore be written using either the cosine or sine function. In this case, the two equations will share the same parameters |\mid a \mid, \mid b\ \mid| and |k.| Only the parameter |h| will be different. Many of the properties of the curve can therefore be obtained the same way.
To analyse the parameters and see an example of the properties of a sinusoidal function with the sine relationship rather than with the cosine relationship, see the following concept sheet: The Properties of the Sine Function (Cosine)