Dans l'animation suivante, tu peux d'abord sélectionner la fonction sinusoïdale de ton choix (sinus ou cosinus), puis tu peux modifier les paramètres |a,| |b,| |h| et |k| et observer leurs effets sur les propriétés de la fonction. Après cette exploration, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions concernant les propriétés de ces fonctions.
Dans le tableau suivant, tu peux observer l'analyse de toutes les propriétés de la fonction cosinus à l'aide d'un exemple.
|
Propriétés |
Fonction sous la forme canonique |
Exemple |
|---|---|---|
|
Règle |
|f(x)=a\cos\big(b(x-h)\big)+k| |
|f(x)=4\cos\big(2(x-\frac{5\pi}{4})\big)+3| |
|
Équation de l'ordonnée moyenne |
|y=k| |
|y=3| |
|
Période |
|P=\dfrac{2 \pi}{\mid b \mid }| |
|P=\dfrac{2\pi}{\mid 2 \mid}=\pi| |
|
Domaine |
|\text{dom }f=\mathbb{R}| |
|\text{dom } f=\mathbb{R}| |
|
Image |
|\text{ima } f = [k-\mid a \mid ,\ k+\mid a \mid]| |
|[-1,7]| |
|
Croissance et décroissance |
|
Puisque |a| est positif, la fonction est décroissante à partir du point |(h,\ k+a)=\left(\frac{5\pi}{4},\ 7\right).| La fonction est croissante sur l'intervalle ||\left[\dfrac{3\pi}{4}+n\pi,\ \dfrac{5\pi}{4}+n\pi\right]||où |n \in \mathbb{Z}| La fonction est décroissante sur l'intervalle ||\left[\dfrac{5\pi}{4}+n\pi,\ \dfrac{7\pi}{4}+n\pi\right]||où |n \in \mathbb{Z}| |
|
Zéros de la fonction |
Ce sont les valeurs de |x| pour lesquelles |f(x)=0.| |x=x_{1}+nP| et |x=x_{2}+nP| où |P| est la période et |n\in \mathbb{Z}| |
|x=5{,}13+n\pi| et |x=5{,}85+n\pi| où |n\in \mathbb{Z}| |
|
Ordonnée à l'origine |
C'est la valeur de |f(0).| |
|f(0)=3| |
|
Signe de la fonction |
Les intervalles où la fonction est positive et où la fonction est négative dépendent des zéros de la fonction, de la période et de l'allure du graphique. |
La fonction est négative sur les intervalles de la forme |[5{,}13+n\pi,\ 5{,}85+n\pi]| où |n\in\mathbb{Z}.| La fonction est positive sur les intervalles de la forme |[5{,}85+n\pi,\ 8{,}28+n\pi]| où |n\in\mathbb{Z}.| |
|
Extrémums |
Maximum : |k\ + \mid a\ \mid| |
Maximum : |7| |
Détermine les propriétés de la fonction cosinus suivante : ||f(x)=2\cos\left( \frac{3\pi}{4}(x-1)\right)+5|| Il peut être utile de tracer le graphique de la fonction.
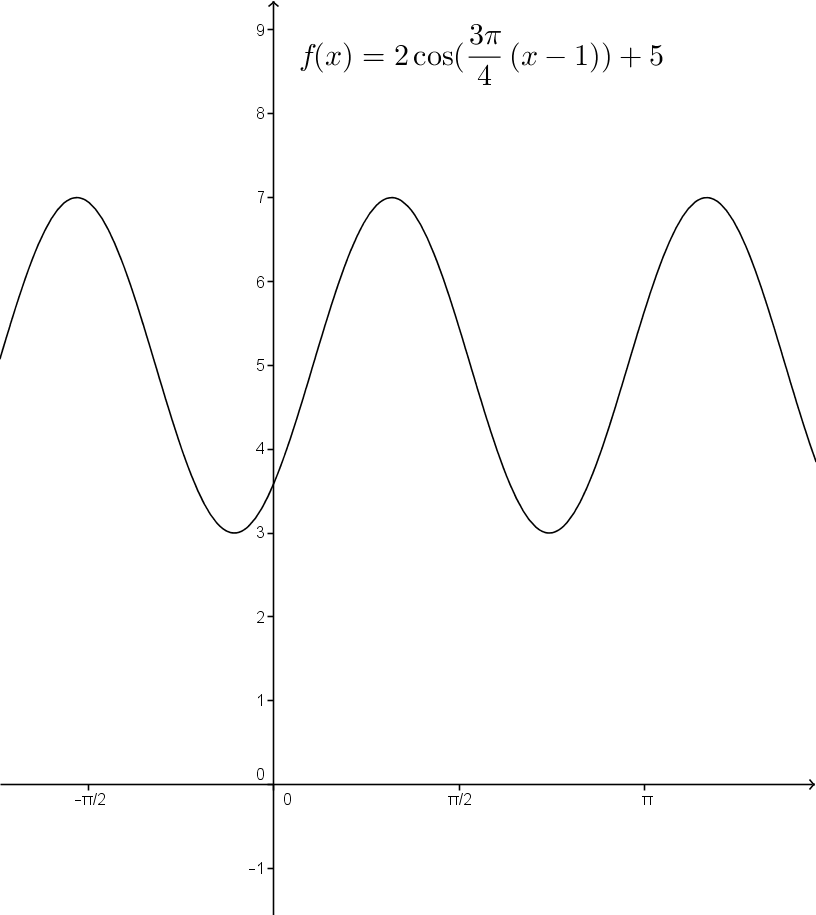
-
L'équation de l'axe d'oscillation de la fonction est |y=5.|
-
Le paramètre |b| valant |\dfrac{3\pi}{4}|, la période de la fonction est |\displaystyle P = \frac{2\pi}{\mid b \mid} = \frac{2\pi}{\mid \frac{3\pi}{4} \mid } = \frac{8}{3}.|
-
Le domaine de la fonction est l'ensemble des nombres réels, c'est-à-dire |\mathbb{R}.|
-
L'image de la fonction est un intervalle de la forme |[k\ - \mid a \mid,\ k\ + \mid a \mid].|
Ici, |a=2| et |k=5.| L'image est donc |[3,\ 7].| -
La variation : le paramètre |a| étant positif, la fonction est décroissante après le point |(h,\ k\ + \mid a \mid),| c'est-à-dire après le point |(1,7).|
-
De manière générale, la fonction est décroissante sur les intervalles de la forme |\left[1 + \dfrac{8n}{3}, \dfrac{7}{3} + \dfrac{8n}{3}\right]| où |n \in \mathbb{Z}.|
-
Elle est croissante sur les intervalles de la forme |\left[\dfrac{7}{3} + \dfrac{8n}{3}, \dfrac{11}{3} + \dfrac{8n}{3}\right]| où |n \in \mathbb{Z}.|
-
-
La fonction n'a aucun zéro. En effet, l'axe d'oscillation étant égal à 5 et l'amplitude valant 2, alors le minimum de la fonction est 3. On peut aussi le constater en faisant des calculs. On remplace |f(x)| par |0.| ||\begin{align}0 &= 2\cos\left(\frac{3\pi}{4}(x-1)\right)+5\\-5 &= 2 \cos\left(\frac{3 \pi}{4}(x-1)\right)\\-2{,}5 &= \cos\left(\frac{3 \pi}{4}(x-1)\right)\end{align}||C'est à cette étape que tout s'arrête. En effet, les valeurs du cosinus sont entre -1 et 1. Donc, le cosinus ne peut jamais valoir |-2{,}5.|
-
L'ordonnée à l'origine se calcule en remplaçant |x| par |0.| ||\begin{align} f(0) &= 2\cos\left(\frac{3\pi}{4}(0-1)\right)+5\\f(0) &= 2\cos\left(-\frac{3\pi}{4}\right) + 5 \\ (\text{il faut} &\text{ consulter le cercle trigonométrique})\\ f(0) &= 2 \times -\frac{\sqrt{2}}{2} + 5 \\ f(0) &= -\sqrt{2} +5\approx 3{,}59 \end{align}||
-
Les signes de la fonction : comme la fonction ne possède aucun zéro, elle est positive sur l'ensemble de son domaine.
-
Les extrémums de la fonction sont :
-
Maximum : |k\ + \mid a \mid\, = 5+2 = 7|
-
Minimum : |k\ - \mid a \mid\, =5-2 = 3|
-
Les fonctions sinus et cosinus sont toutes les deux des fonctions sinusoïdales. Une même courbe peut donc être écrite avec le rapport cos ou avec le rapport sin. Dans ce cas, les deux règles partageront les mêmes paramètres |\mid a \mid, \mid b\ \mid| et |k.| Seul le paramètre |h| sera différent. Plusieurs propriétés de la courbe sont donc obtenues de la même façon.
Pour comprendre l'analyse des paramètres et pour voir un exemple d'étude des propriétés d'une fonction sinusoïdale écrite avec le rapport sin plutôt qu'avec le rapport cos, consulte la fiche suivante : Les propriétés de la fonctions sinus