In the following animation, experiment with the parameters |a,| |b,| |c,| |h,| and |k| of the exponential function and observe their effects on the function’s properties. Afterwards, read the concept sheet to learn more about the properties of the function.
|
Properties |
Basic exponential function |
Exponential function in standard form |
|---|---|---|
|
Equation |
||f(x)=c^x|| |
||f(x)= ac^{b(x-h)}+k|| Asymptote at |y=k| |
|
Domain |
|\mathbb{R}| or depending on the context. |
|\mathbb{R}| or depending on the context. |
|
Range |
The range is the interval|(0,+\infty).| |
If |a>0| and |b>0,| the range is the interval |(k,+\infty).| |
|
|x|-intercept (zero of the function) |
|\forall x,\ f(x)\neq 0| |
Exists if |a>0| and |k<0| or |a<0| and |k>0.| |
|
Sign of the Function |
With |c>0| and |c\neq 1,| the function is positive over all its domain. |
According to the equation of the function and the existence of an |x|-intercept. |
|
|y|-intercept |
If |x=0,| so |f(x)=1.| |
This is the value of |f(x)| when |x=0.| |
|
Extrema |
None or depending on the context. |
None or depending on the context. |
|
Increasing interval |
If |c>1,| the function is increasing on its domain. |
If |c>1| and |a| and |b| have the same sign. If |0<c<1| and |a| and |b| have opposite signs. |
|
Decreasing interval |
If |0<c<1,| the function decreases on its domain. |
If |0<c<1| and |a| and |b| have If |c>1| and |a| and |b| have opposite signs. |
Determine the different properties of the function |f(x)=-2 (3)^{x+1}+3.|
It is useful to sketch a graph to clarify the problem.
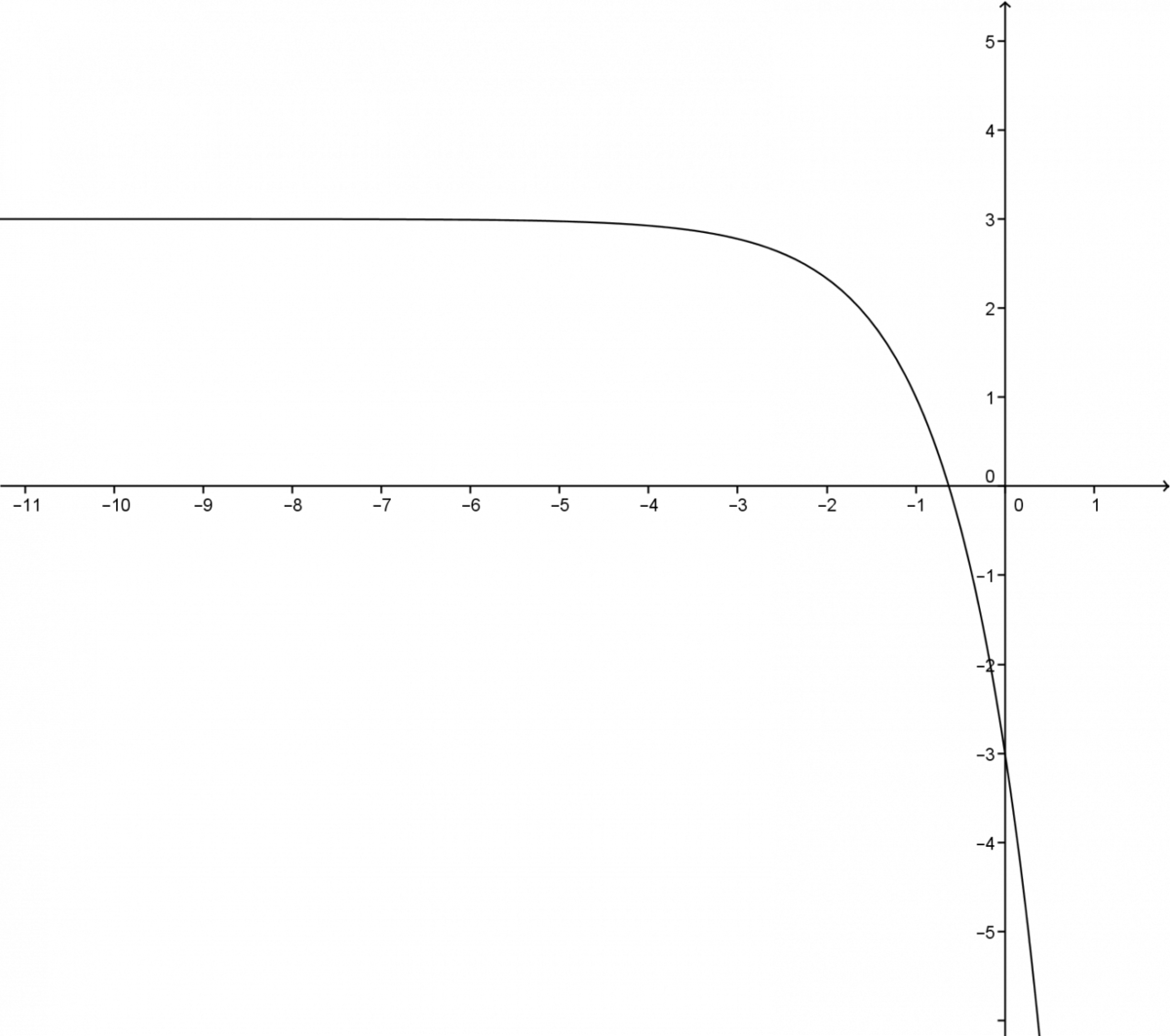
-
The asymptote of this function is |y=3.|
-
The domain of the function is the set of real numbers, denoted by |\mathbb{R}.|
-
The range of the function is the interval |(-\infty, 3).|
-
The |x|-intercept of the function is calculated by replacing |f(x)| with |0| and isolating |x.| ||\begin{align} 0 &= -2 (3)^{x+1}+3\\-3 &= -2 (3)^{x+1}\\ 1.5 &= 3^{x+1}\end{align}|| As shown here, use the logarithm to isolate |x|. ||\begin{align}\log_3 1.5 &= x+1\\ \log_3 1.5 - 1 &= x\\ -0.63 &\approx x\end{align}||
So the |x|-intercept is approximately |-0.63.| -
The sign of the function is positive when |x| is in the interval |(-\infty;-0.63]| and negative when |x| is in the interval |[-0.63; +\infty).|
-
To calculate the |y|-intercept, replace |x| with |0.| ||\begin{align}f(0) &= -2 (3)^{0+1} + 3\\ f(0) &= -3\end{align}|| The |y|-intercept of the function is |-3.|
-
The function has no extrema.
-
The variation: the function is decreasing everywhere, since |c>1,| and |a| and |b| have opposite signs.