The inverse (or preimage) of a quadratic (or second-degree polynomial) function is not a function. Here is how to find it.
To find the inverse of a quadratic function using a graph, simply draw the line with equation |y = x|. Then find the curve that is symmetrical with respect to this axis. The new parabola is the inverse of the quadratic function. Here are two examples.
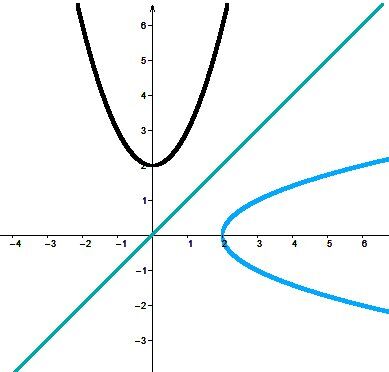
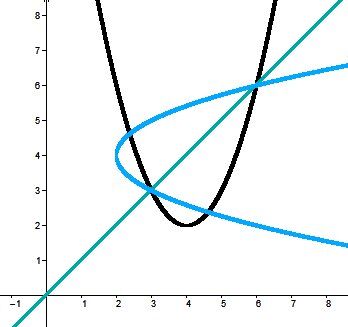
The definition of a function states that for the same value of |x|, there cannot be more than one value of |y|.
By carefully observing the graphs, we conclude that the inverses are not functions, because for the same |x|-value, there are two different |y|-values.
The inverse of a quadratic function is not a function as mentioned above. However, it is possible to determine the equation of the inverse.
The inverse of a quadratic function is formed by two branches of a square root function.
-
Invert |x| and |y|.
-
If the equation of the function is in the general form, complete the square (stop at this stage when a difference of squares or a positive term is obtained after factoring the perfect square trinomial).
-
If the equation of the function is in standard form, the |y| can be isolated directly.
It is helpful to look at two examples.
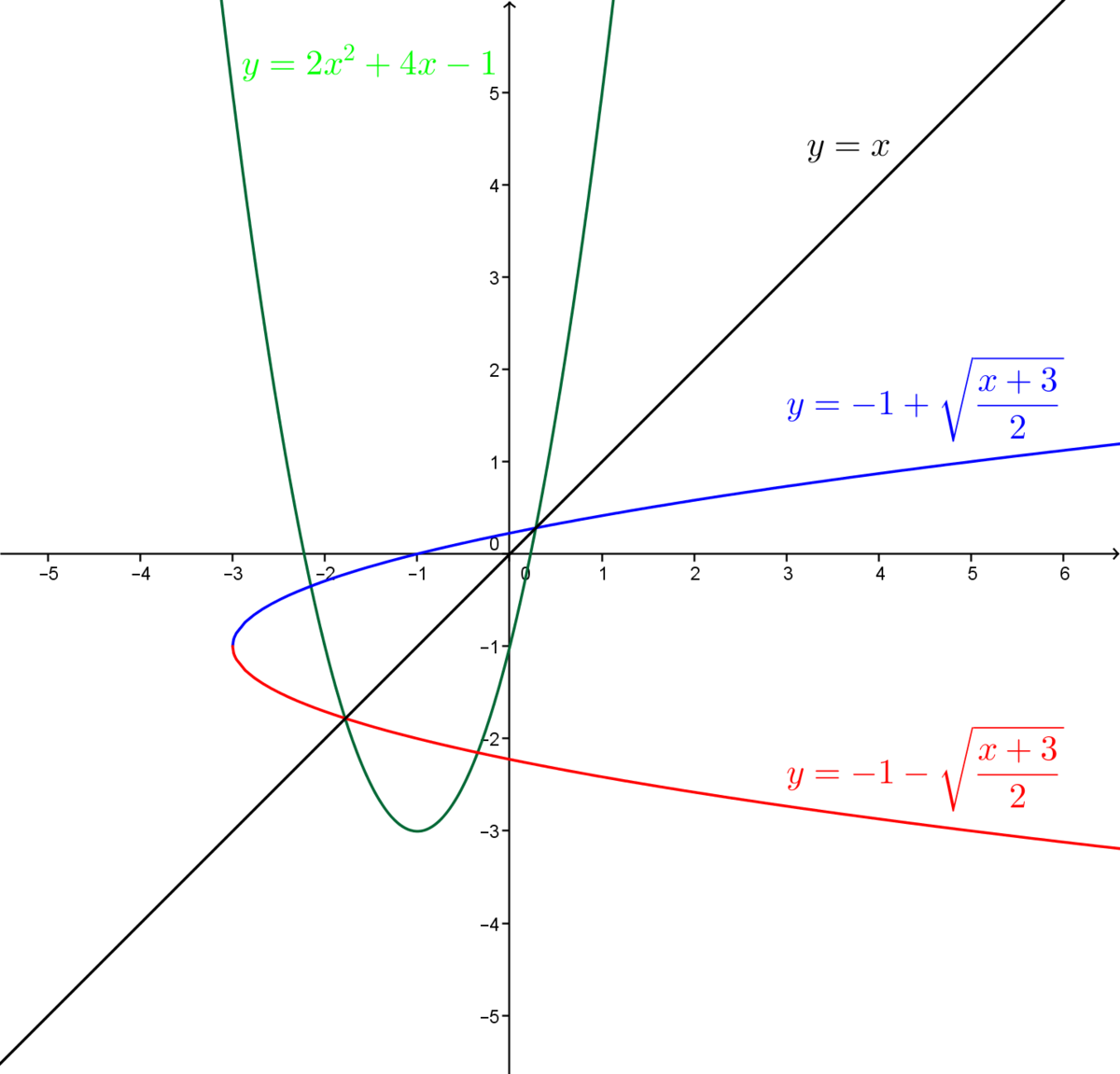
Consider the function |y=2x^2+4x-1|.
First interchange |x| and |y|.
||y=2x^2+4x-1 \rightarrow x=2y^2+4y-1||
Here, it is necessary to complete the square on the right-hand side.
||x=2(y^2+2y-\frac{1}{2})||
|b=2|, so |\displaystyle \left( \frac{b}{2}\right)^2 = \left( \frac{2}{2} \right)^2 = 1| has to be added and subtracted.
||x=2(y^2+2y+1 -\frac{1}{2} -1)||
||x=2((y+1)^2-\frac{3}{2}))||
Stop completing the square here.
At this stage, isolate the expression |(y+1)^2|.
||x=2(y+1)^2-3||
||x+3 = 2(y+1)^2||
||\displaystyle \frac{x+3}{2} = (y+1)^2||
Then take the square root of both sides of the equation. Don’t forget the |\pm| on the left side.
||\pm \displaystyle \sqrt{\frac{x+3}{2}} = y+1||
||-1 \pm \displaystyle \sqrt{\frac{x+3}{2}} = y||
This is the inverse of the starting function. This inverse has two branches.
Here is the graph representing the initial function and its inverse.
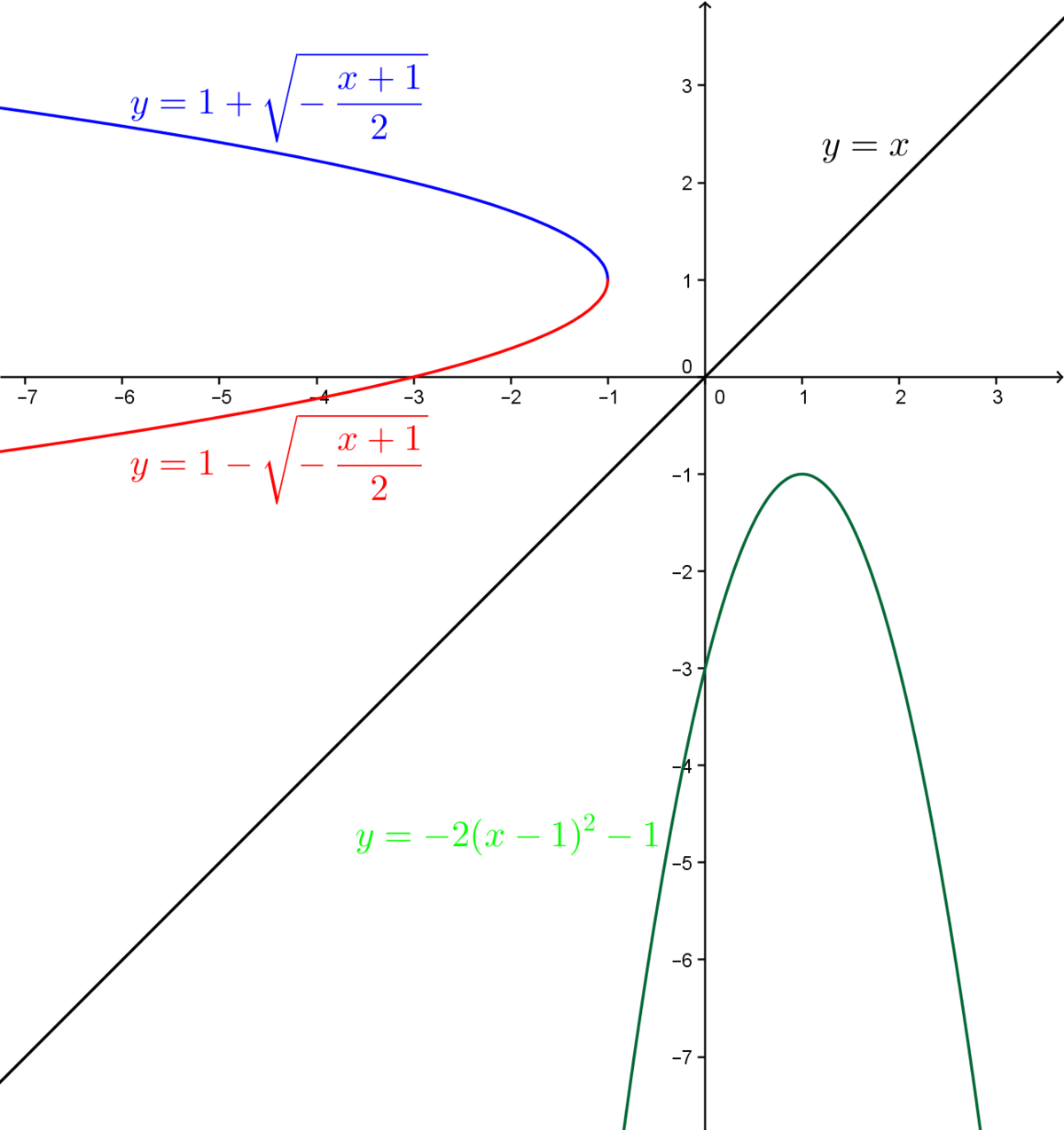
Consider the function |y=-2(x-1)^2-1|.
First interchange |x| and |y|.
||y=-2(x-1)^2-1 \rightarrow x=-2(y-1)^2-1||
We can directly isolate |y|.
||x+1 = -2(y-1)^2||
||\displaystyle - \frac{x+1}{2} = (y-1)^2||
At this stage, take the root of both sides of the equation. Don’t forget the |\pm| in front of the root.
||\displaystyle \pm \sqrt{-\frac{x+1}{2}} = y-1||
||\displaystyle 1 \pm \sqrt{-\frac{x+1}{2}}=y||
Here is the inverse of the initial function which has two branches.
Here is the graph representing the initial function and its inverse.