La réciproque d'une fonction polynomiale du second degré n'est pas une fonction. Toutefois voici comment la trouver :
Pour trouver la réciproque d’une fonction polynomiale du second degré à l’aide d’un graphique, il nous suffit de tracer la droite d’équation |y = x|, puis d’effectuer une symétrie par rapport à cet axe. La parabole ainsi trouvée est la réciproque de notre fonction polynomiale du second degré. Voici deux exemples :
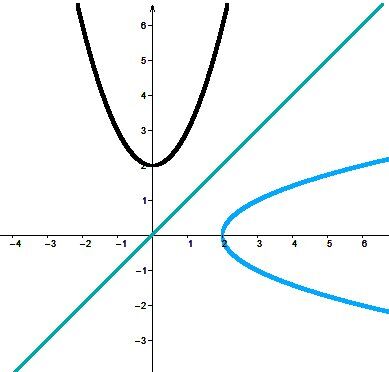
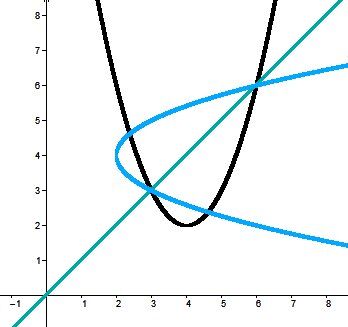
La définition d'une fonction stipule que pour une même valeur de |x|, il ne peut y avoir plus d'une valeur de |y|.
Si on observe attentivement les graphiques, on se rend compte que les réciproques ne sont pas des fonctions, car pour un même |x|, il y a deux valeurs différentes pour les |y|.
La réciproque d'une fonction polynomiale du second degré n'est pas une fonction comme il a été mentionné plus haut. Il est toutefois possible de déterminer l'équation de la réciproque.
La réciproque d'une fonction polynomiale du second degré est constituée de deux branches d'une fonction racine carrée.
-
Intervertir |x| et |y|.
-
Si l'équation de la fonction est sous la forme générale, il faut compléter le carré (il faut arrêter à l'étape où l'on arrive à une différence de carrés ou à un terme positif, après avoir factorisé le trinôme carré parfait).
-
Si l'équation de la fonction est sous la forme canonique, on peut isoler |y| directement.
Il est utile de regarder deux exemples.
Soit la fonction |y=2x^2+4x-1.|
Il faut d'abord intervertir |x| et |y.| ||y=2x^2+4x-1 \rightarrow x=2y^2+4y-1||
Rendu ici, il faut compléter le carré dans le membre de droite. ||x=2\left(y^2+2y-\dfrac{1}{2}\right)||
Le |b=2,| donc ce qu'on doit ajouter et retrancher est |\left(\dfrac{b}{2}\right)^2 = \left(\dfrac{2}{2} \right)^2 = 1.| ||\begin{align}x &= 2\left(y^2+2y+1 -\dfrac{1}{2} -1\right) \\ x &= 2\left((y+1)^2-\dfrac{3}{2}\right) \end{align}||Il faut arrêter la complétion ici.
À cette étape, on isole l'expression |(y+1)^2.| ||\begin{align} x &= 2(y+1)^2-3\\ x+3 &= 2(y+1)^2 \\ \dfrac{x+3}{2} &= (y+1)^2 \end{align}||
On extrait la racine carrée des deux côtés de l'égalité. Il ne faut pas oublier le |\pm| du côté gauche. ||\begin{align} \pm \sqrt{\dfrac{x+3}{2}} &= y+1 \\ -1 \pm \sqrt{\dfrac{x+3}{2}} &= y \end{align}||
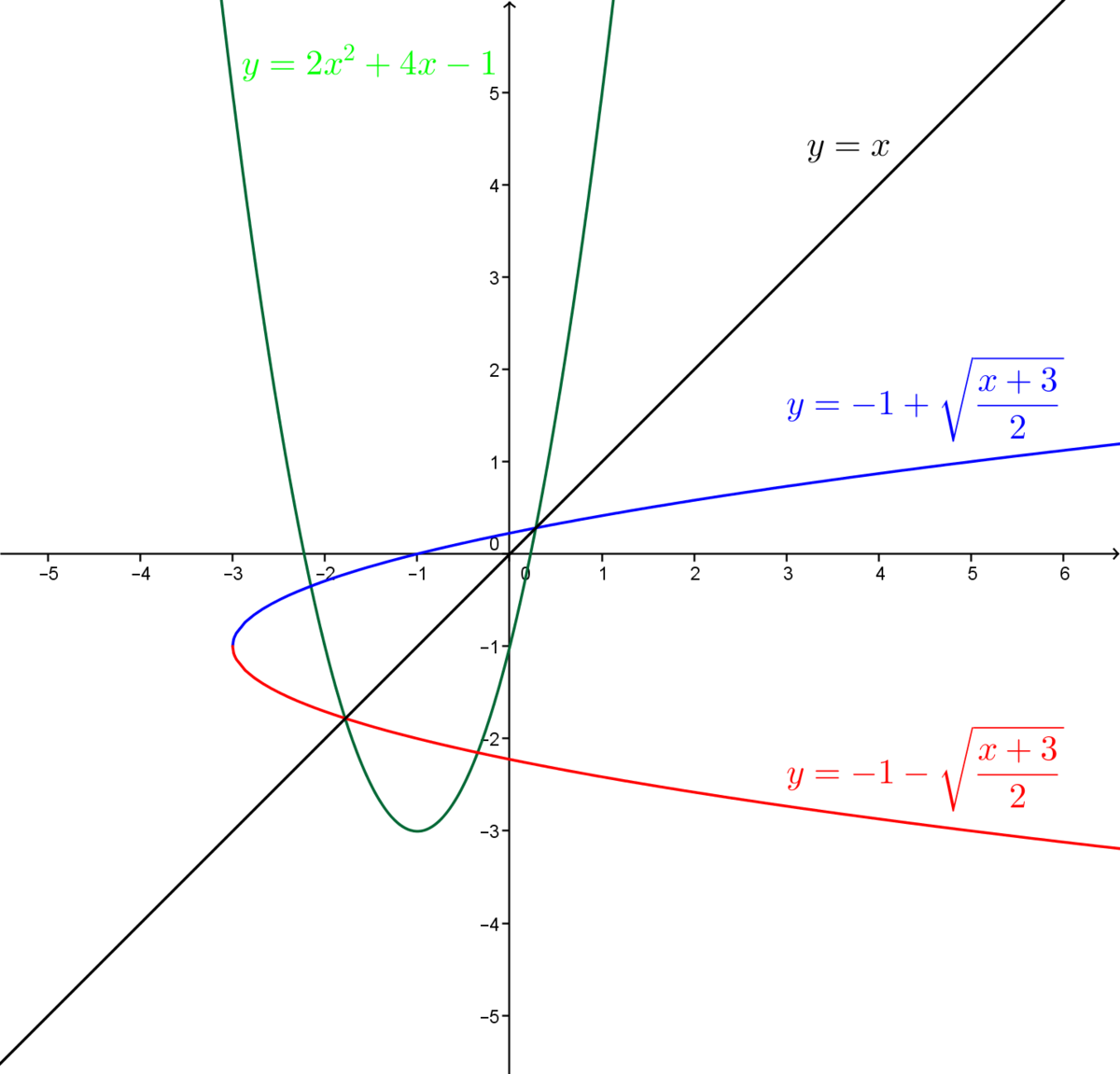
On a donc l'équation de la réciproque de la fonction de départ. Cette réciproque comporte deux branches.
Voici le graphique de la fonction initiale et de sa réciproque.
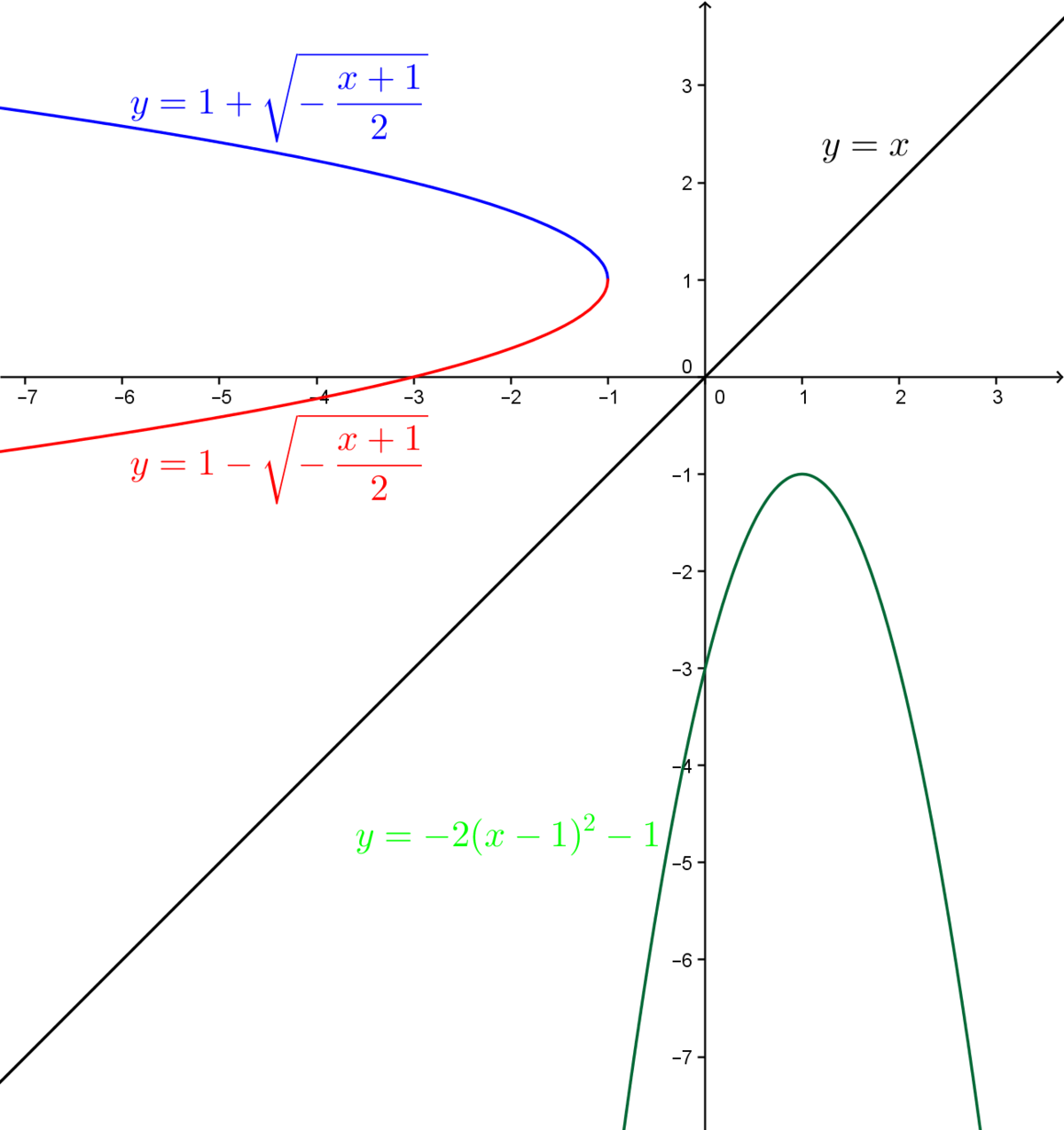
Soit la fonction |y=-2(x-1)^2-1.|
Il faut d'abord intervertir |x| et |y.| ||y=-2(x-1)^2-1 \rightarrow x=-2(y-1)^2-1||
On peut isoler directement le |y.| ||\begin{align} x+1 &= -2(y-1)^2 \\ - \dfrac{x+1}{2} &= (y-1)^2 \end{align}||
Rendu ici, on extrait la racine carrée des deux côtés de l'égalité. Il ne faut pas oublier le |\pm| du côté gauche. ||\begin{align} \pm \sqrt{-\dfrac{x+1}{2}} &= y-1 \\ 1 \pm \sqrt{-\frac{x+1}{2}} &= y \end{align}||
On a donc l'équation de la réciproque de notre fonction de départ. Cette réciproque comporte deux branches.
Voici le graphique de la fonction initiale et de sa réciproque.