Adding the parameters |a,| |b,| |h,| and |k| to the basic function |f(x)=\cos(x)| results in what is called the standard form (also called the transformed form) of the cosine function.
The standard form of a cosine function is: ||f(x)=a \cos\big(b(x-h)\big)+k|| where |a,| |b,| |h,| and |k| are real numbers that function as parameters.
Note: The parameters |a| and |b| are always non-zero.
Experiment with the parameters |a,| |b,| |h,| and |k| in the interactive animation to see their effects on the cosine function. Observe the changes that take place on the transformed curve (in green) compared to the base function (in black). Afterwards, keep reading the concept sheet to learn more about each of the parameters.
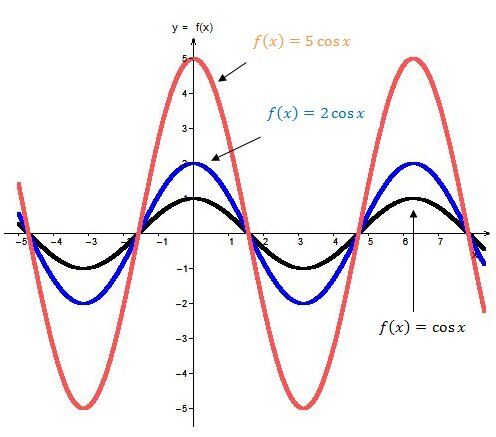
When |{\mid}a{\mid}>1|
The larger the absolute value of the parameter |a|, the greater the amplitude of the cosine function.
When |0< {\mid}a{\mid} < 1|
The smaller the absolute value of the parameter |a| (nearer |0|), the smaller the amplitude of the cosine function.
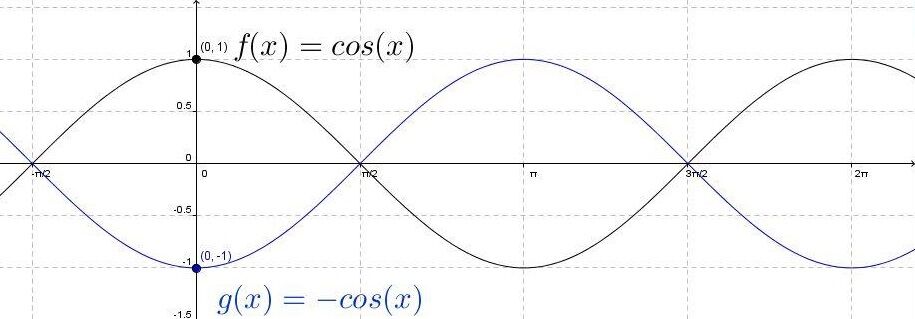
When |a| is positive |(a>0)|
The point |(h,k+a)| is a maximum of the curve and the function decreases after this point.
When |a| is negative |(a<0)|
The point |(h,k+a)| is a minimum of the curve and the function increases after this vertex.
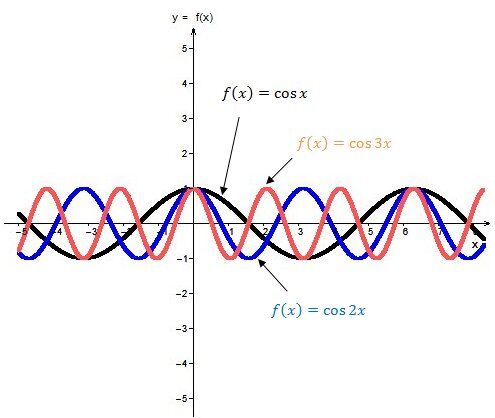
When |{\mid}b{\mid} >1|
The larger the absolute value of the parameter |b|, the smaller the period and the smaller the distance between two maxima or minima of the function.
When |0< {\mid}b{\mid} <1|:
The smaller the absolute value of the parameter |b| (closer to |0|), the greater the period and the distance between two maxima or two minima of the function.
A cosine function with the same value of |b|, but the opposite sign, superimposes onto the other function.

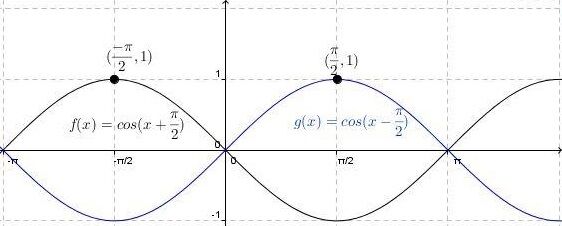
The parameter |h| is responsible for the horizontal displacement of the curve. This is also called the phase shift in a sinusoidal function.
When |h| is positive |(h>0)|
The curve of the cosine function moves to the right.
When |h| is negative |(h<0)|
The curve of the cosine function moves to the left.
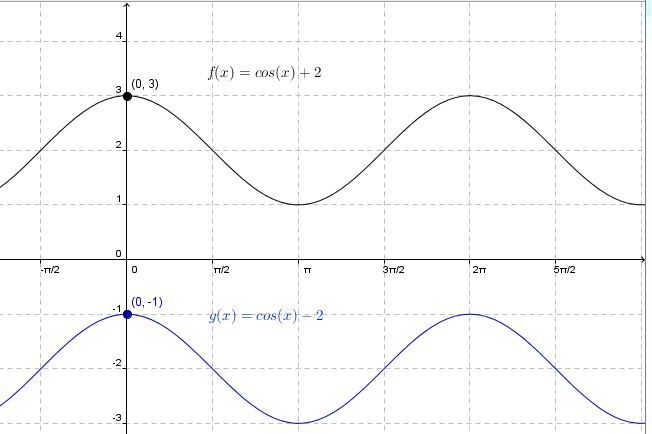
When |k| is positive |(k>0)|
The cosine function moves upwards.
When |k| is negative |(k<0)|
The cosine function moves downwards.