This concept sheet illustrates the different parameters of a quadratic function in its standard form, general form, and factored form.
The basic form of a quadratic (or second-degree polynomial) function is |f(x)=x^{2}.|
Transforming this basic shape results in an equation with different parameters.
Standard form: |f(x)=a(x−h)^2+k| where |h| and |k| are the coordinates of the vertex.
General form: |f(x)=ax^2+bx+c| where |c| is the |y|-intercept.
Factored form: |f(x)=a(x−x_1)(x−x_2)| where |x_1| and |x_2| are the zeroes of the parabola.
Note: The parameter |a| is always the same no matter the form, and it can never be zero.
In the following animation, modify the parameters of the quadratic function. Observe the changes that take place on the transformed curve (in black) and compare them with the base function (in green). Take notice of how changing the parameters affects the function’s properties. Afterwards, keep reading the concept sheet to understand the parameters of each form.
The parameter |a| is responsible for the vertical stretching or scaling of the parabola.
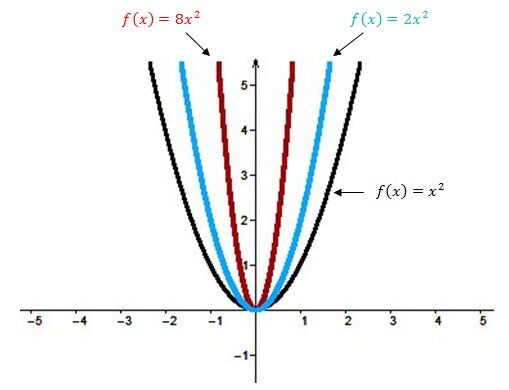
When |a| is greater than |1\ (a>1)|
The larger the parameter |a|, the narrower the opening of the parabola, i.e. the two branches of the curve approach the |y|-axis. Therefore, the function is stretched vertically.
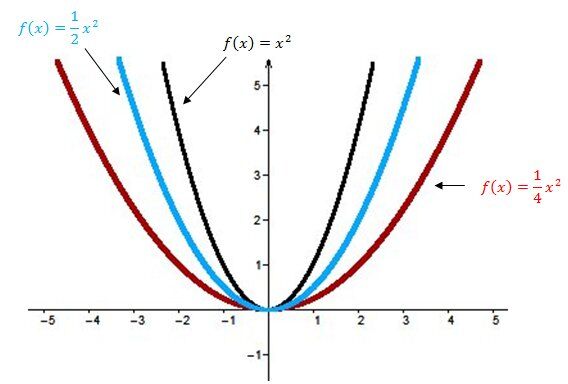
When |a| is between |0| and |1\ (0<a<1)|
The smaller |a| is (closer to |0|), the larger the opening of the parabola, i.e. the two branches of the curve move away from the |y|-axis. Therefore, the function is compressed vertically.
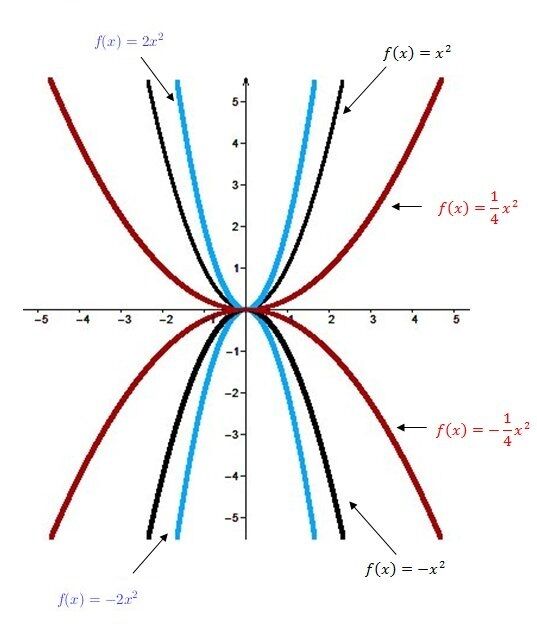
When |a| is positive |(a>0)|
The parabola opens upwards.
When |a| is negative |(a<0)|
The parabola opens downwards.
Standard form: |f(x)=a(x−h)^2+k| where |a|, |h|, and |k| are the parameters of the function.
Note: The parameter |a| cannot be zero.
When |h| is positive |(h>0)|
The curve of the quadratic function is translated to the right.
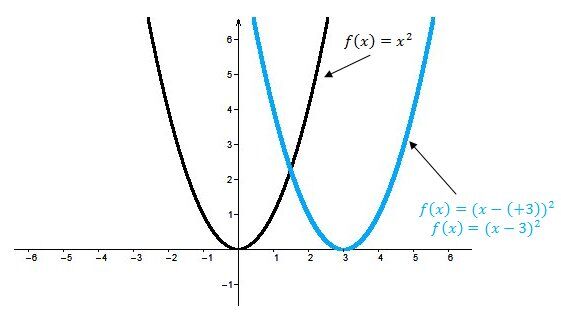
When |h| is negative |(h<0)|
The curve of the quadratic function is translated horizontally to the left.
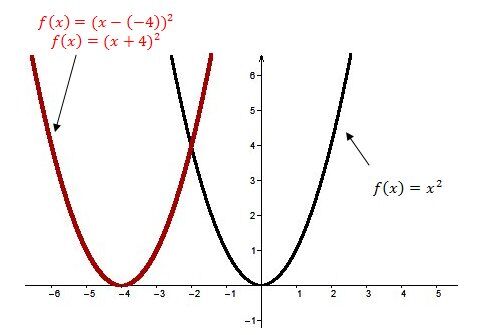
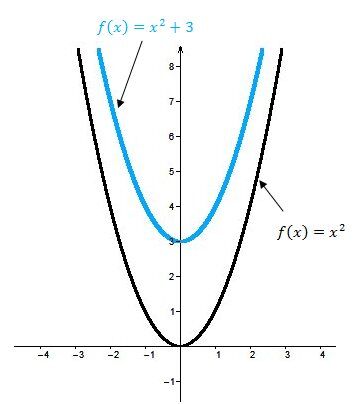
When |k| is positive |(k>0)|
The curve of the quadratic function is translated vertically upwards.
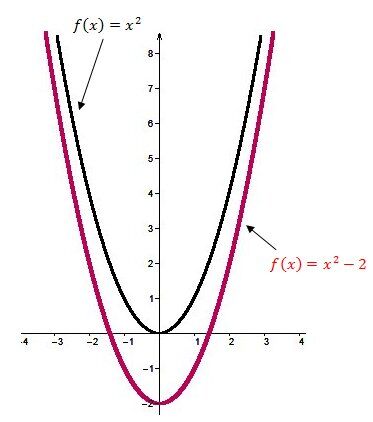
When |k| is negative |(k<0)|
The curve of the quadratic function is translated vertically downwards.
In standard form, the parameters |h| and |k| provide the coordinates of the vertex of the parabola in the Cartesian plane.
||\text{Vertex}=(h,k)||
General form: |f(x)=ax^2+bx+c| where |a|, |b|, and |c| are the parameters of a function.
Note: The parameter |a| cannot equal zero.
In the general form, the parameter |a| is the same as in factored and standard form. Therefore, it has the same effects on the parabola. See the following examples.
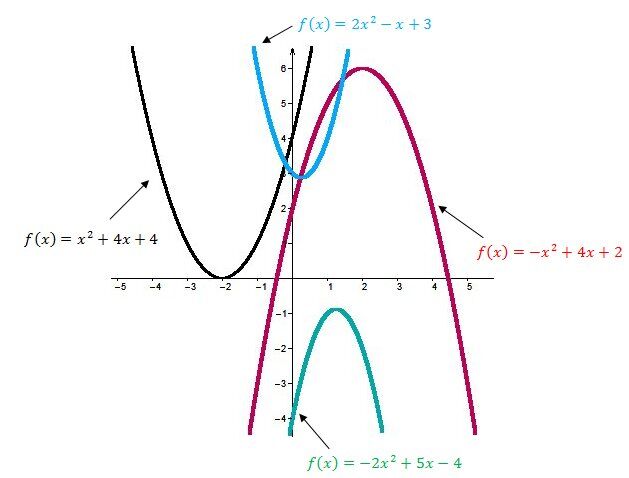
When we change the parameter |b| of a quadratic function in general form, the vertex is translated on a slant (it follows a line that has the shape of a parabola). Be careful, as the influence of the parameter |b| on the graph depends first and foremost on the sign of the parameter |a|. The direction of the parabola’s movement will be different depending on whether the parameter |a| is positive or negative.
When |b| is positive |(b>0)|
The parabola moves to the left and downwards if |a>0|. It moves to the right and upwards if |a<0|.
In the following example, the values of |a| and |c| are fixed |(a=1| and |c=0)| and the value of |b| varies.
When |b| is negative |(b<0)|
The parabola moves to the right and downwards if |a>0|. It moves to the left and upwards if |a<0|.
In the following example, the values of |a| and |c| are fixed |(a=1| and |c=0)| and the value of |b| varies.
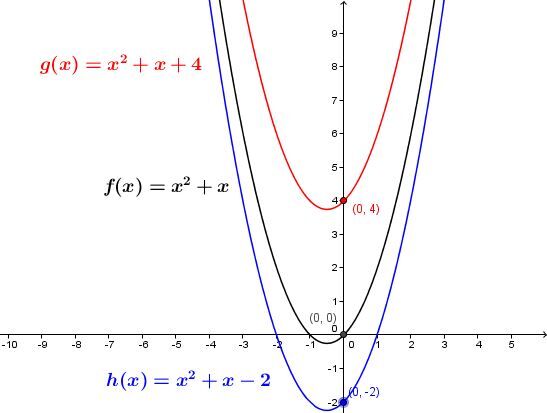
In general form, the parameter |c| gives the value of the |y|-intercept, i.e. the value of |y| when |x=0.|
If the value of the parameter |c| increases, the curve is translated upwards. If the value of |c| decreases, the curve is translated downwards.
Factored form: |f(x)=a(x−{ x }_{ 1 })(x−{ x }_{ 2 })| where |a,| |{ x }_{ 1 },| and |{ x }_{ 2 }| are the parameters of the function.
Note: The parameter |a| cannot be zero.
In factored form, the parameter |a| is the same as in general form and standard form. Therefore, it has the same effects on the parabola.
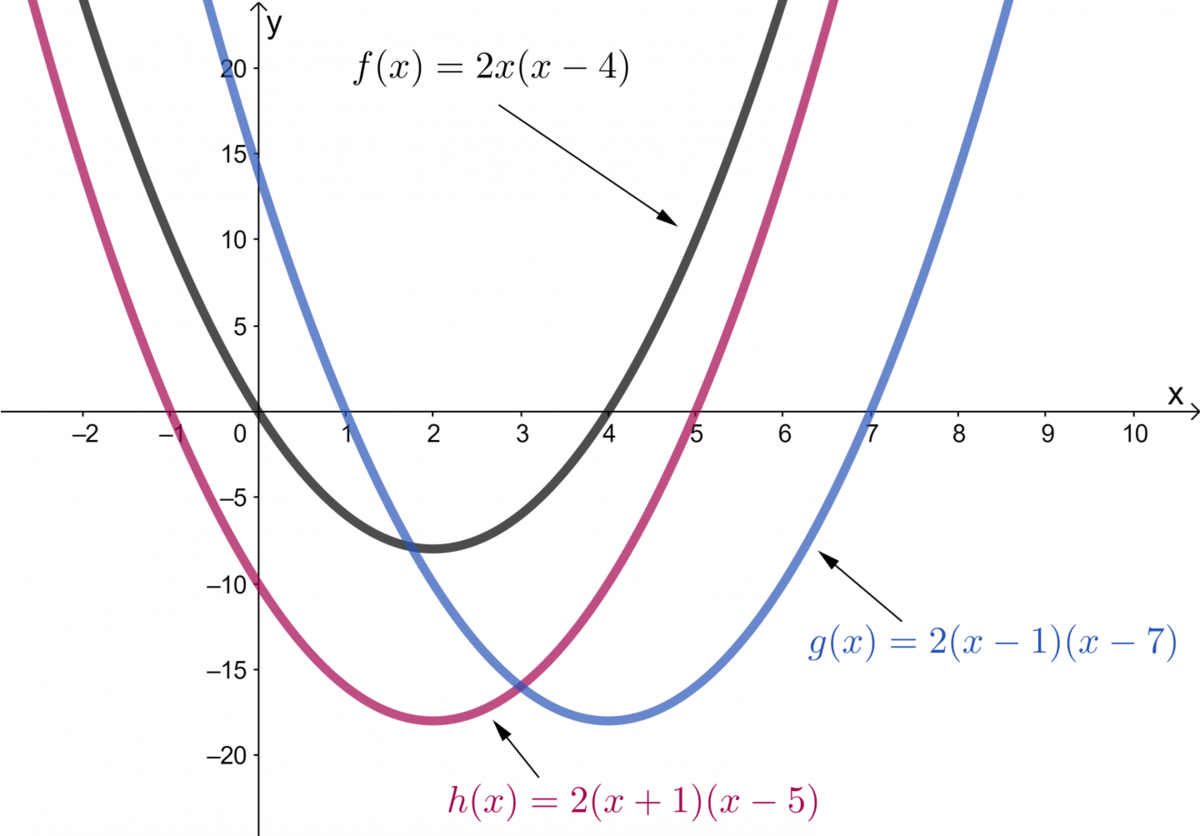
In factored form, the parameters |{ x }_{ 1 }| and |{ x }_{ 2 }| give the value of the zeroes of the function, i.e. the values of |x| when |y=0.|
A quadratic function cannot be written in factored form when the curve does not cross the |x|-axis, i.e. when there are no zeroes.