After adding the parameters |a,| |b,| |h|, and |k| to the basic square root function |f(x)=\sqrt{x},| we obtain the standard form (also called the transformed form) of the square root function.
The standard form of a square root function is: ||f(x)=a\sqrt{b(x-h)}+k||
where |a,| |b,| |h,| and |k| are real numbers that function as parameters.
Note: The parameters |a| and |b| are always non-zero.
Experiment with the parameters |a|, |b|, |h|, and |k| in the interactive animation to see their effects on the square root function. Observe the changes that take place on the transformed curve (in black) compared to the basic function (in blue). Notice the effect of modifying the parameters on the function’s properties. Afterwards, keep reading the concept sheet for more information about each parameter.
When |{\mid}a{\mid}>1|:
The square root function is stretched vertically compared to the graph of the basic function. In essence, the larger the absolute value of the parameter |a|, the closer the square root function is to the |y|-axis.

When |0< {\mid}a{\mid} < 1|:
The square root function shrinks vertically relative to the graph of the base function. The smaller (nearer to |0|) the absolute value of the parameter |a|, the closer the curve of the square root function is to the |x|-axis.
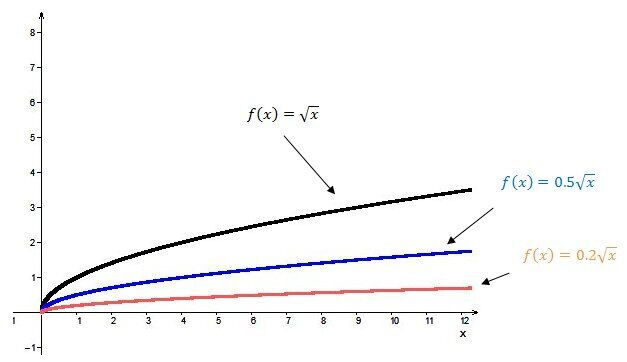
When |a| is positive |(a>0)|:
The square root function is increasing.
When |a| is negative |(a<0)|:
The square root function is decreasing.

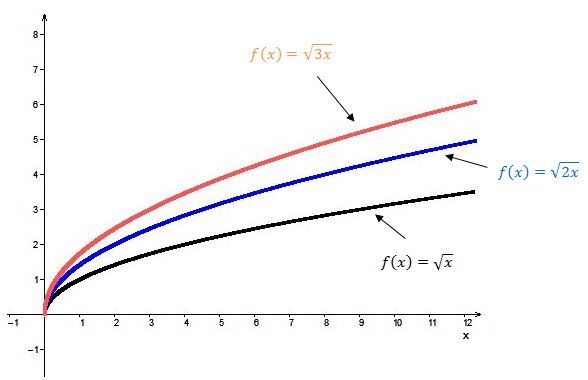
When |{\mid}b{\mid} >1|:
The square root function undergoes a horizontal contraction relative to the base function. The larger the absolute value of the parameter |b|, the more the branch of the graph of the square root function moves away from the |x|-axis.
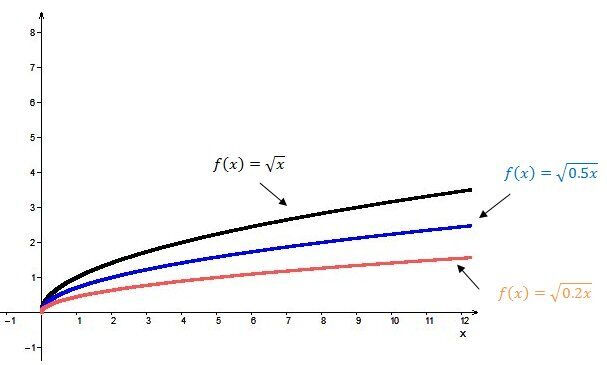
When |0< {\mid}b{\mid} < 1|:
The square root function is stretched horizontally relative to the base function. The smaller (closer to |0|) the absolute value of the parameter |b|, the closer the square root function is to the |x|-axis.
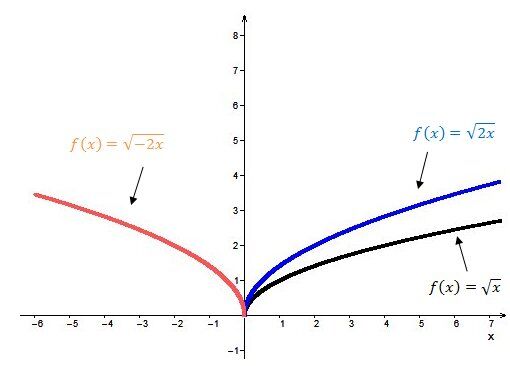
When |b| is positive |(b>0)|:
The graph of the square root function is oriented to the right.
When |b| is negative |(b<0)|:
The graph of the square root is oriented to the left.
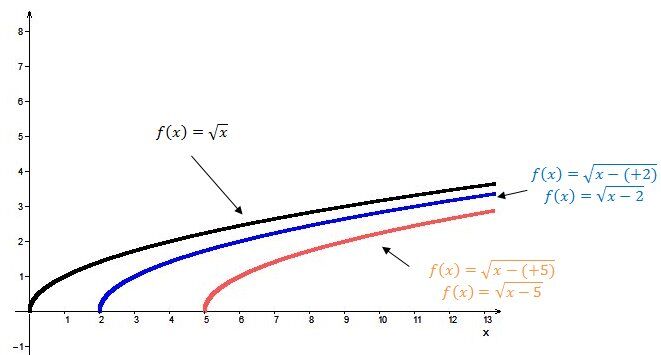
When |h| is positive |(h>0)|:
The curve of the function moves to the right.
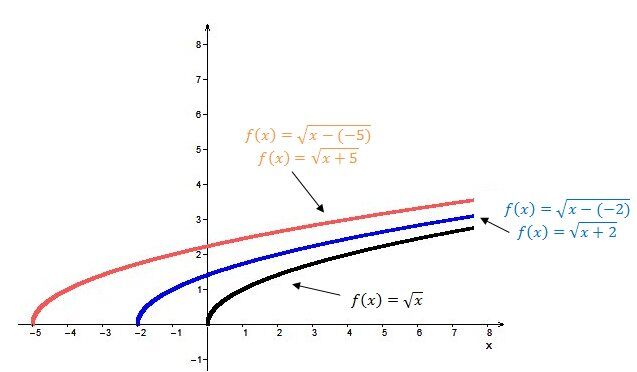
When |h| is negative |(h<0)|:
The curve of the function moves to the left.
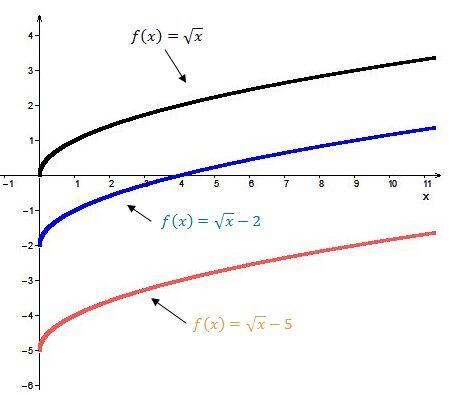
When |k| is positive |(k>0)|:
The curve of the function moves upwards.

When |k| is negative |(k<0)|:
The curve of the function moves downward.