A pattern rule is a mathematical relationship used to find the value of each term in a sequence.
To describe certain sequences, a pattern rule can be established. This is an algebraic equation that enables you to quickly find the value of a term in a sequence using its rank.
The pattern rule of an arithmetic sequence can be written as follows.
|\text{Term = pattern} \times \text{term rank + term when rank is 0}|
In the formula, we can change the word pattern to rate of change.
|\text{Term = rate of change} \times \text{term rank + term when rank is 0}|
You can also write the formula using an abbreviated form.

Use the following procedure to find the pattern rule of an arithmetic sequence.
-
Determine the rate of change by calculating the difference between two consecutive terms.
-
Determine the value of the term when the rank is equal to |0| (rank 0).
-
Write the pattern rule.
Consider the following table of values.
-
Determine the rate of change
The distance between two consecutive terms represents the pattern of the rule.
|7 - 5 = 2|
|9 - 7 = 2|
|11 - 9 = 2|
Therefore, the rate of change is +2. Thus, write: |t = 2\times n + \text{rank} \,0.| -
Determine the value of rank 0
Method 1:
Find the number to add or subtract by replacing the term and the rank by a point (number pair) in the table of values.Take the point |(3, 9).| Replace |t| by |9| and |n| by |3.|
|9= 2\times 3 + \text{rank }\,0|
|9= 6 + \text{rank }\,0|Replace the rank 0 with |3| to respect the equality.
|9=6+3|
Method 2:
The value of the term located at rank 0 can be determined. To do so, subtract the rate of change from the term located at rank 1.
|5 - (+2) = 3|
Therefore, rank 0 is |3.| -
Write the rule
Therefore, the rule is |t=2n+3.|
Consider the following table of values.
-
Determine the rate of change
The distance between two consecutive terms represents the pattern of the rule.
|-14 - (-12) = -2|
|-16 - (-14) = -2|
|-18 - (-16) = -2|
Therefore, the rate of change is |-2.| Then, write: |t = -2\times n + \text{rank }\,0.| -
Determine the value of rank 0
Find the number to add or subtract by replacing the term and the rank by a point (number pair) in the table of values.
Take the point |(1, -12).| Replace |t| by |-12| and |n| by |1.|
|-12= -2\times 1 + \text{rank }\,0|
|-12= -2 + \text{rank }\,0|Replace the rank 0 with |-10| to respect the equality.
|-12=-2+ -10| -
Write the rule
Therefore, the rule is |t=-2n-10.|
The pattern rule of a geometric sequence can be written in the following form.
|\text{Term} = 1^{st}\,\text{term}\times \text{rate of change}^{(\text{term rank} - 1)}|
The rule can be simplified by using variables.
|t = 1^{st}\,\text{term}\times \text{rate of change}^{(n - 1)}|
Follow these steps to find the pattern rule of a geometric sequence.
-
Determine the rate of change between two consecutive terms.
-
Determine the first term of the sequence.
-
Write the pattern rule.
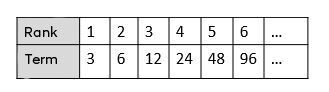
Consider the table of values below.
-
Determine the rate of change
To go from one term to the next, we multiply by a factor of |2.| Therefore, the rate of change is |2.|
-
Determine the first term
The first term in the sequence is |3.|
-
Write the rule
Therefore, the rule is |t = 3\times 2^{(n - 1)}.|
To find the term that occupies the |12^{\text{th}}| rank using the following rule: |t = 4n + 7,| we replace |n| by its value |(12).| ||\begin{align} t &= 4(12) + 7 \\ t &= 48 + 7 \\ t &= 55 \end{align}|| The |12^{\text{th}}| term in the sequence is |55.|
To find the rank of the term |167| using the following rule: |t = 4n + 7,| we replace |t| by its value |(167).| ||\begin{align} 167 &= 4n + 7 \\ 167 \color{#ec0000}{- 7} &= 4n + 7 \color{#ec0000}{- 7} \\ 160 &= 4n \\ \color{#ec0000}{\dfrac{\color{black}{160}}{4}} &= \color{#ec0000}{\dfrac{\color{black}{4n}}{4}} \\ 40 &= n \end{align}|| Term |167| is located at the |40^{\text{th}}| rank.
Pour valider ta compréhension à propos des situations de proportionnalité, des situations inversement proportionnelles et des suites arithmétiques, consulte la MiniRécup suivante.
