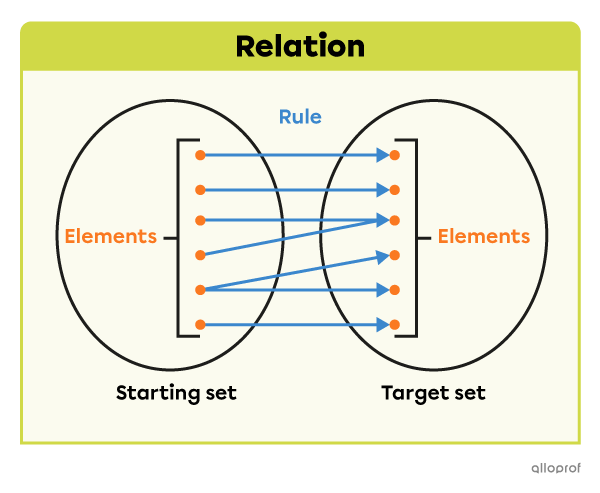
In mathematics, a relation is a statement that defines a link between several elements. Each relation has a rule that establishes the correspondence between the elements of a starting set and the elements of a target set.
A function is a relationship between 2 variables where each value of the independent variable (starting set) is associated with only one value of the dependent variable (target set).
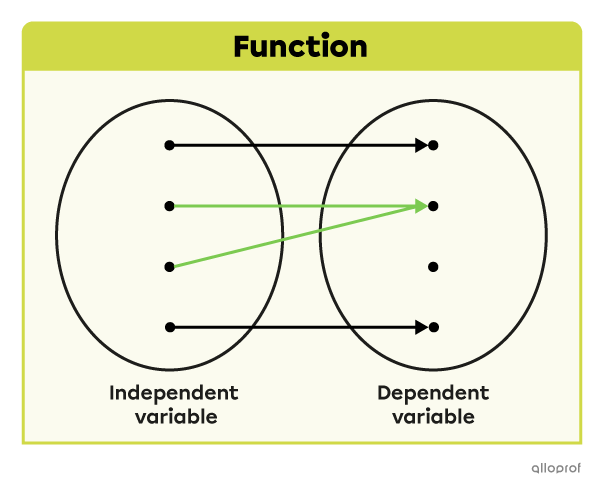
This relation is a function, since each element of the independent variable is associated with only one element of the dependent variable.
This relation is not a function, since one element of the independent variable is associated with several elements of the dependent variable.
You can determine if a relation is a function by looking at its graph. To do so, simply apply the vertical line test.
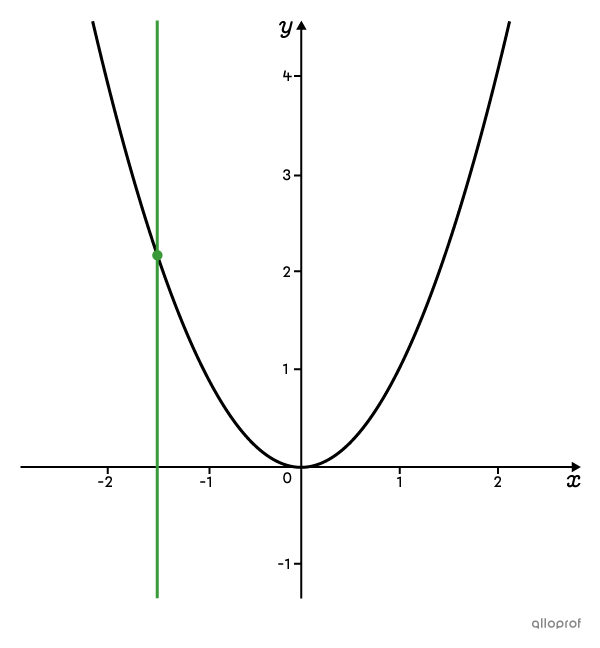
This relation is a function, since the vertical line intersects the curve at only one point, no matter where it is placed.
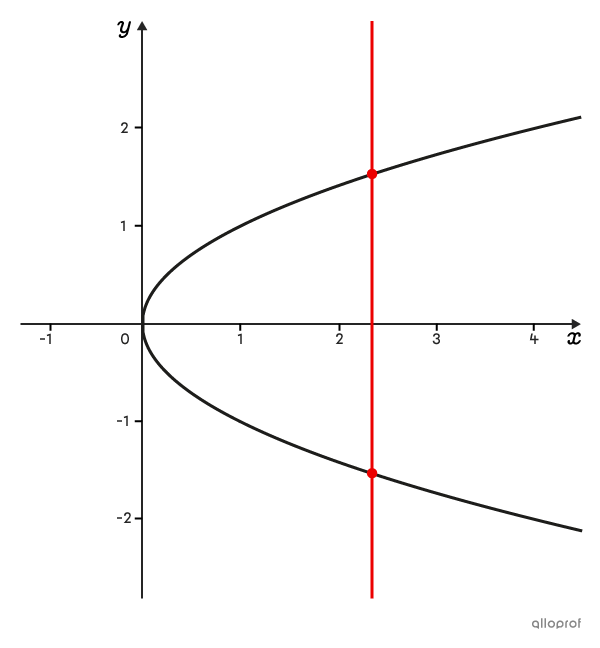
This relation is not a function, since the vertical line can be placed so that it intersects the curve at 2 different points.
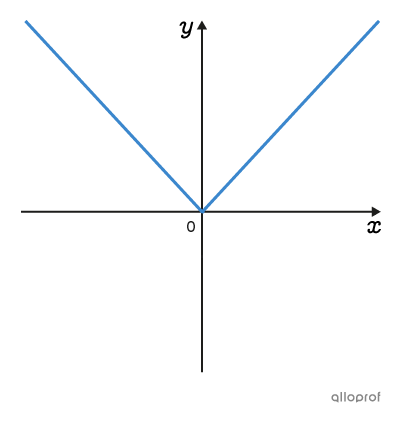
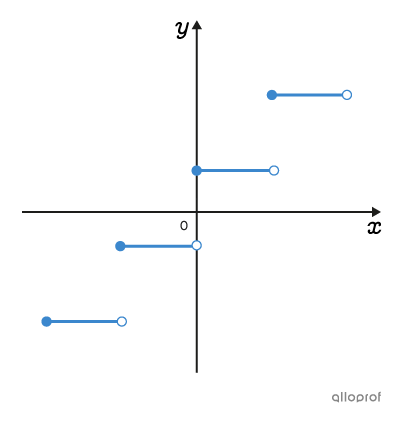
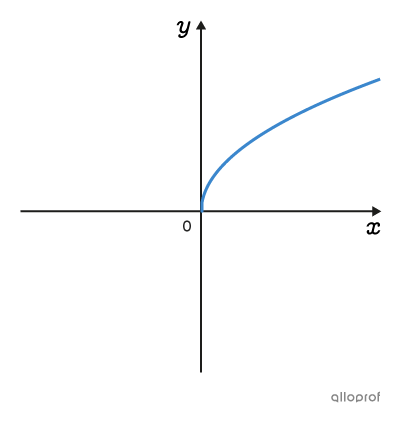
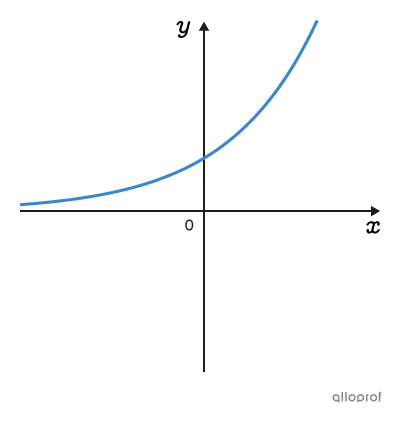
A multitude of situations can be represented graphically by several function families. Functions of the same family have graphs and rules with common characteristics.
Click on the images to know more.
Constant Function
Linear Function
Quadratic Function
Rational Function
Absolute Value Function
Step Function
Square Root Function
Exponential Function
Logarithmic Function
Piecewise Function
Periodic Function
Trigonometric Function
We often write the rule of a function as |y=\text{rule}.| However, we also use the notation |f(x)=\text{rule,}| which reads "|f| of |x|" and means "the value of |f| based on the value of |x|."
In other words, |y| and |f(x)| are 2 equivalent notations used to designate the dependent variable.
Consider the function |y=2x+3,| which can also be written as |f(x)=2x+3.|
To calculate the value of the function when |x=5,| the calculations can be written in the 2 following ways:
||\begin{align}y&=2x+3\\y&=2(5)+3\\y&=13\end{align}||
||\begin{align}f(x)&=2x+3\\f(5)&=2(5)+3\\f(5)&=13\end{align}||
Therefore, the pair |(5,13)| belongs to this function.
Functions can also be written using functional notation. This notation is used to define a function by specifying its starting set, its target set and its rule of correspondence.
||\begin{align}f:\ \ \begin{gathered}\text{Starting}\\\text{set}\end{gathered}\ \ \,&\rightarrow\quad\ \ \ \begin{gathered}\text{Target}\\\text{set}\end{gathered}\\[3pt]\begin{gathered}\text{Independent}\\\text{variable}\end{gathered}&\mapsto\begin{gathered}\text{Rule of }\\\text{correspondence}\end{gathered}\end{align}||
Consider the function |f(x)=3x+4.| Using functional notation, this function can be written as follows:||\begin{align}f:\mathbb{R}&\rightarrow\mathbb{R}\\[3pt]x&\mapsto3x+4\end{align}||The starting set is |\mathbb{R},| the target set is also |\mathbb{R}| and the rule of correspondence is |3x+4.| In addition, the independent variable is |x| and the dependent variable is |f(x).|
This functional notation is read as follows:
"Function |f| goes from |\mathbb{R}| to |\mathbb{R}| and associates an element |x| from the starting set with an element |3x+4| of the target set."
To check your understanding of the functions interactively, consult the following Crash Course:
