Operations on functions are performed the same way operations on numbers are performed.
Given the two real functions |f| and |g,| their sum is defined as follows.
||(f+g)(x)=f(x)+g(x)||
The domain of the sum of functions corresponds to the intersection of the domains of the functions in question. If there is a denominator, the restrictions on it must be included.
Function |k| is defined by |k(x)=x+1| and function |l| is defined by |l(x)=2x+1.| The sum of the functions results in the following.
||\begin{eqnarray*} (k+l)(x)&=&k(x)+l(x) \\
&=& (x+1)+(2x+1) \\
&=& 3x+2 \end{eqnarray*}||
Function |k|’s domain corresponds to |\mathbb{R}.| Function |l|’s domain also corresponds to |\mathbb{R}.| Therefore, the function given by |k+l|’s domain will correspond to the intersection of the two initial domains. Function |k+l|’s domain is |\mathbb{R}.|
Function |i| is defined by |i(x)=x+2| and function |j| is defined by |j(x)=\sqrt{x}.| The sum of the functions results in the following.
||\begin{eqnarray*} (i+j)(x) &=& i(x)+j(x) \\
&=&(x+2)+\sqrt{x} \\
&=& x+\sqrt{x}+2 \end{eqnarray*}||
Function |i|’s domain corresponds to |\mathbb{R}| and function |j|’s domain corresponds to |\mathbb{R}^{+}.| The function’s domain |i+j| will then correspond to the intersection of the two initial domains. Therefore, function |i+j|’s domain is |\mathbb{R}^{+}.|
Function |f| is defined by |f(x)=\dfrac{2}{x}| and function |g| is defined by |g(x)=2x.| The sum of the functions results in the following. ||\begin{align} (f+g)(x) &= f(x) + g(x) \\ &=\dfrac{2}{x} + 2x \\ &= \dfrac{2}{x} +\dfrac{2x^2}{x} \\ &= \dfrac{2+2x^2}{x} \\ &= \dfrac{2(1+x^2)}{x} \end{align}||
Function |f|’s domain is |\mathbb{R} \backslash \lbrace 0 \rbrace| and function’s domain |g|’s domain is |\mathbb{R}.| Therefore, the domain of their sum is |\mathbb{R} \backslash \lbrace 0 \rbrace \cap \mathbb{R} = \mathbb{R} \backslash \lbrace 0 \rbrace.|
Graphically, the sum of functions is obtained by adding the ranges of the functions of the problem.
In the first example, if we make a table of values for the functions |k(x)=x+1,| |l(x)=2x+1,| and their sum |k+l,| the result is the following.
|
|x| |
|k(x)| |
|l(x)| |
|(k+l)(x)| |
|---|---|---|---|
|
|1| |
|2| |
|3| |
|5| |
|
|2| |
|3| |
|5| |
|8| |
|
|3| |
|4| |
|7| |
|11| |
|
|4| |
|5| |
|9| |
|14| |
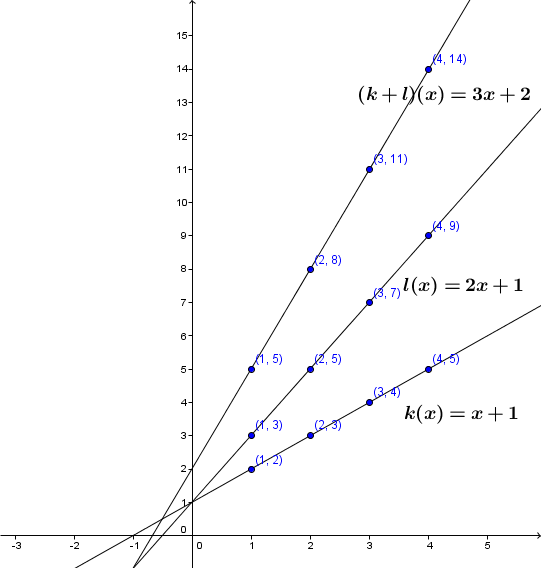
Function |k+l| is increasing and its domain is |\mathbb{R}.|
To obtain the graph of a sum of functions, add the ranges of each of the functions.
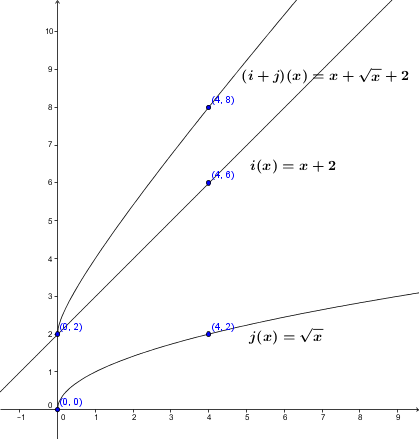
The function |i+j| is an increasing function whose domain is |\mathbb{R}^{+}.|
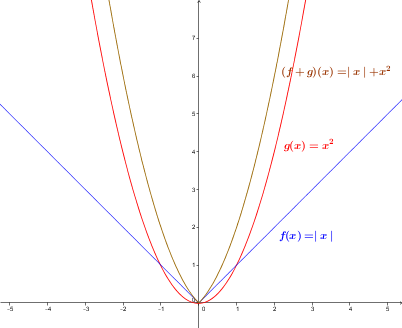
Function |f| is defined by |f(x)= {\mid}x{\mid}| and function |g| is defined by |g(x)=x^2.|
To confirm you understand of operations on functions, see the following interactive CrashLesson:
