On effectue des opérations sur les fonctions de la même manière que l’on effectue des opérations sur les nombres.
Étant donné deux fonctions réelles |f| et |g|, on définit la somme de celles-ci comme suit :||(f+g)(x)=f(x)+g(x)||
Le domaine de la fonction somme correspond à l’intersection des domaines des fonctions sur lesquelles on opère. S'il y a un dénominateur, il faut inclure les restrictions sur ce dernier.
Soit la fonction |k| définie par |k(x)=x+1| et la fonction |l| définie par |l(x)=2x+1|. La somme de ces fonctions donnera le résultat suivant : ||\begin{eqnarray*} (k+l)(x)&=&k(x)+l(x) \\
&=& (x+1)+(2x+1) \\
&=& 3x+2 \end{eqnarray*}||
Le domaine de la fonction |k| correspond à |\mathbb{R}| et le domaine de la fonction |l| correspond aussi à |\mathbb{R}|. Le domaine de la fonction |k+l| correspondra alors à l’intersection des deux domaines initiaux. Le domaine de la fonction |k+l| sera donc |\mathbb{R}|.
Soit la fonction |i| définie par |i(x)=x+2| et la fonction |j| définie par |j(x)=\sqrt{x}|. La somme de ces fonctions donnera le résultat suivant : ||\begin{eqnarray*} (i+j)(x) &=& i(x)+j(x) \\
&=&(x+2)+\sqrt{x} \\
&=& x+\sqrt{x}+2 \end{eqnarray*}||
Le domaine de la fonction |i| correspond à |\mathbb{R}| et le domaine de la fonction |j| correspond à |\mathbb{R}^{+}|. Le domaine de la fonction |i+j| correspondra alors à l’intersection des deux domaines initiaux. Le domaine de la fonction |i+j| sera donc |\mathbb{R}^{+}|.
Soit la fonction |f| définie par |f(x)=\dfrac{2}{x}| et la fonction |g| définie par |g(x)=2x|. La somme de ces fonctions donne le résultat suivant : ||\begin{align} (f+g)(x) &= f(x) + g(x) \\ &=\dfrac{2}{x} + 2x \\ &= \dfrac{2}{x} +\dfrac{2x^2}{x} \\ &= \dfrac{2+2x^2}{x} \\ &= \dfrac{2(1+x^2)}{x} \end{align}||
Le domaine de la fonction |f| est |\mathbb{R} \backslash \lbrace 0 \rbrace| et le domaine de la fonction |g| est |\mathbb{R}|. Ainsi, le domaine de la somme est |\mathbb{R} \backslash \lbrace 0 \rbrace \cap \mathbb{R} = \mathbb{R} \backslash \lbrace 0 \rbrace.|
Graphiquement, la somme de fonctions s'obtient en additionnant les images des fonctions en jeu.
Dans le premier exemple, si on fait une table des valeurs des fonctions |k(x)=x+1| , |l(x)=2x+1| et de la somme de |k+l| on obtient :
| |x| | |k(x)| | |l(x)| | |(k+l)(x)| |
|---|---|---|---|
| 1 | 2 | 3 | 5 |
| 2 | 3 | 5 | 8 |
| 3 | 4 | 7 | 11 |
| 4 | 5 | 9 | 14 |
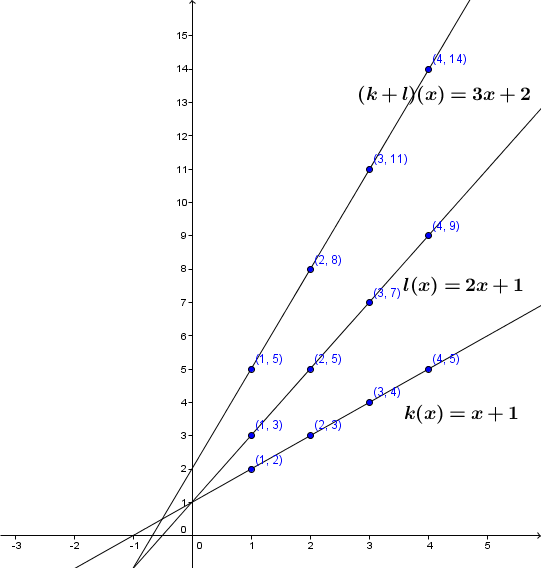
La fonction |k+l| est croissante et son domaine est |\mathbb{R}|.
Pour obtenir l’image de cette somme de fonctions, il suffit d’additionner les images de chacune des fonctions.
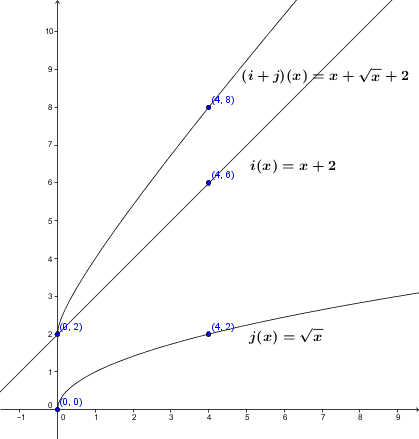
La |i+j| est aussi une fonction croissante et son domaine est |\mathbb{R}^{+}|.
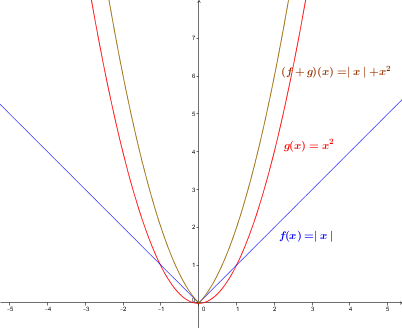
Soient la fonction |f| définie par |f(x)= {\mid}x{\mid}| et la fonction |g| définie par |g(x)=x^2.|
Pour valider ta compréhension des opérations sur les fonctions de façon interactive, consulte la MiniRécup suivante :
