Some types of problems, for example those involving networks, often require minimizing or maximizing cost or distance. In these cases it is necessary to find the tree of minimum or maximum value that connects all the vertices of a graph.
Steps for solving a problem using the tree of minimum value
-
Rewrite the vertices of the graph, next to the initial graph.
-
Draw the line segment with the least weight.
-
Among the remaining edges, repeat the second step until all the vertices of the graph are connected, without obtaining a simple circuit.
-
Calculate the weight of the resulting tree if necessary.
Steps for solving a problem using the tree of maximum value
-
Rewrite the vertices of the graph, next to the initial graph.
-
Draw the line segment with the greatest weight.
-
Among the remaining edges, repeat the second step until all the vertices of the graph are connected without obtaining a simple circuit.
-
Calculate the weight of the resulting tree if necessary.
Sidewalk construction
A contractor must connect 5 buildings with concrete sidewalks. He submits a preliminary estimate for the cost of the operation, represented by the weighted graph on the right. The costs are in the thousands of dollars.
We want to minimize the total cost of building the sidewalks by connecting all the buildings.
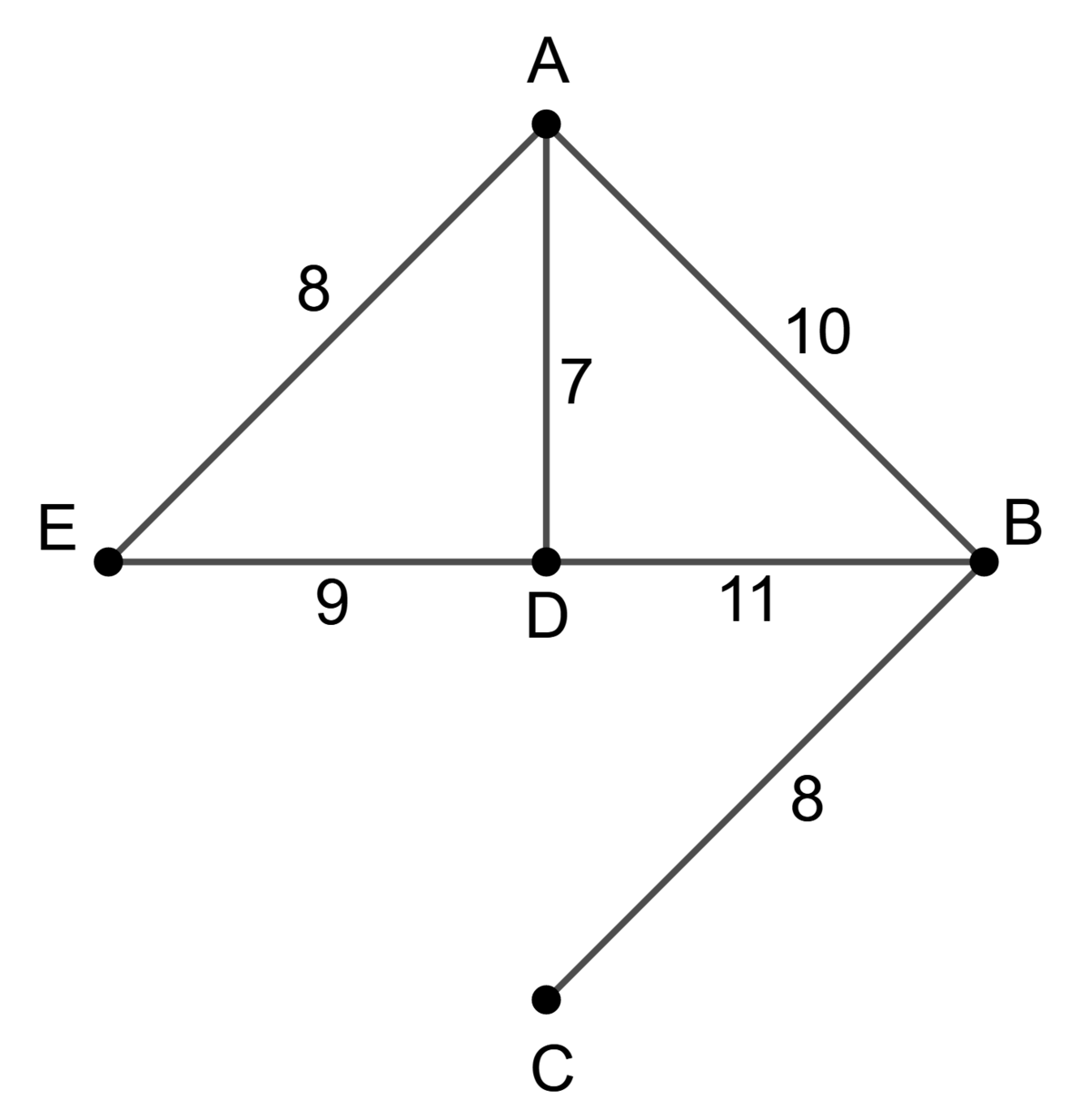
Solution
Since we want to minimize the costs, we need to determine the tree of minimum value.
Step 1
Rewrite the vertices of the graph, next to the initial graph.
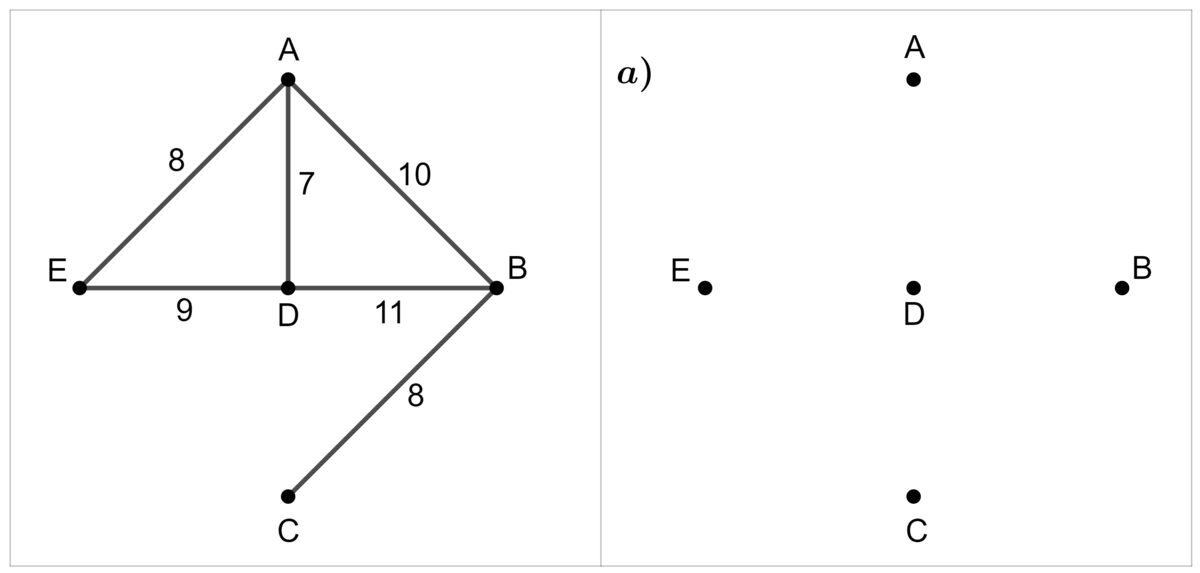
Step 2
Draw the edge with the lowest weight.
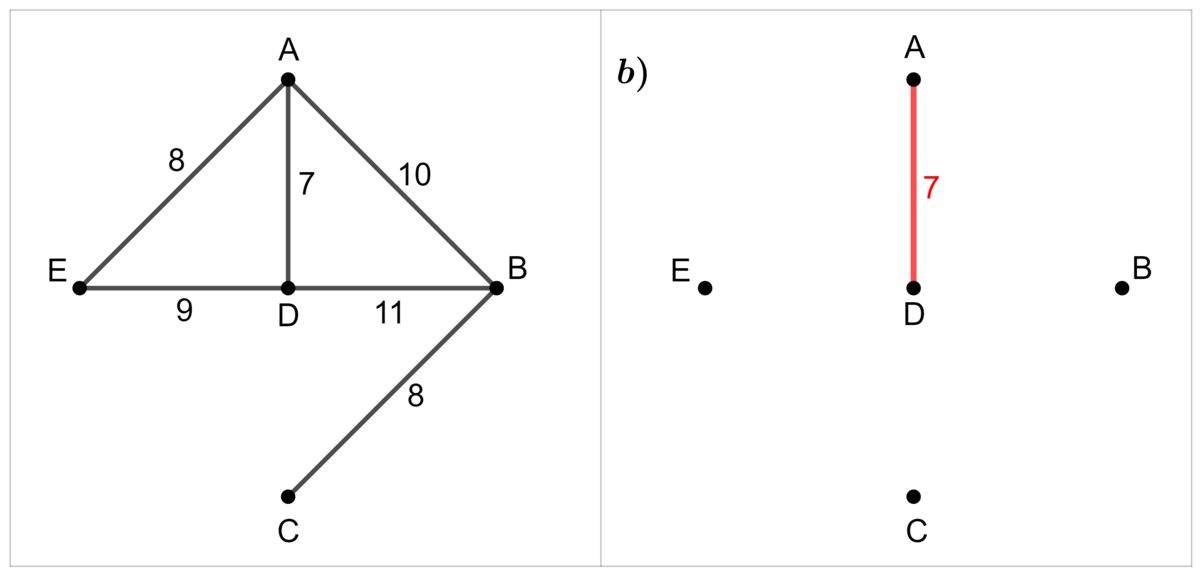
Step 3
Among the remaining edges, repeat the second step until all the vertices of the graph are connected, without obtaining a simple circuit.
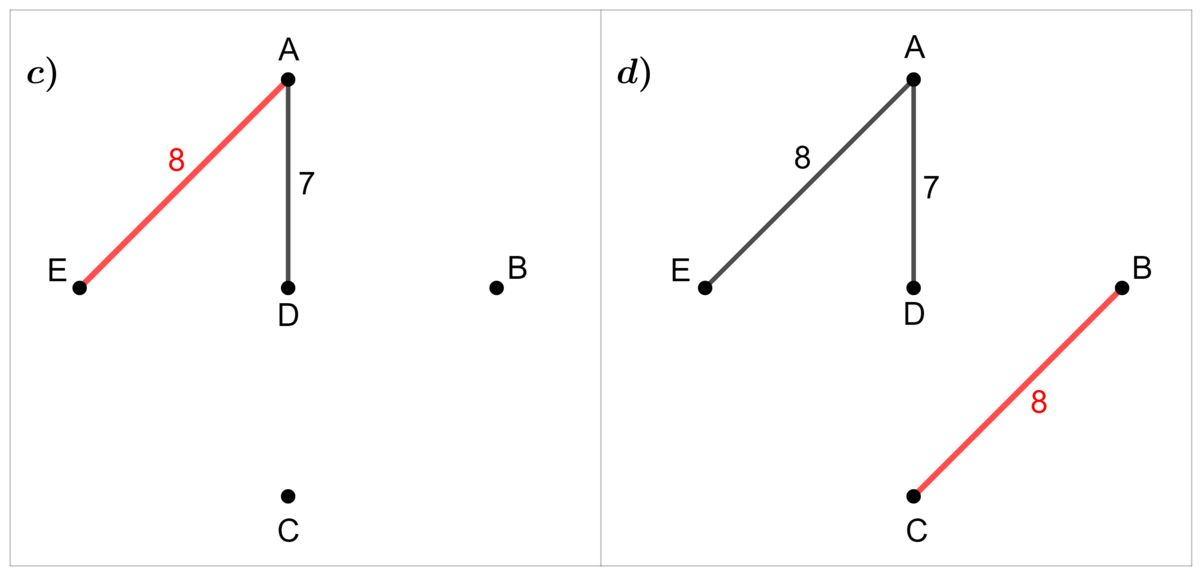
Since two edges have the same value, we select them both if they do not create a simple circuit. Then, we continue with the next value.
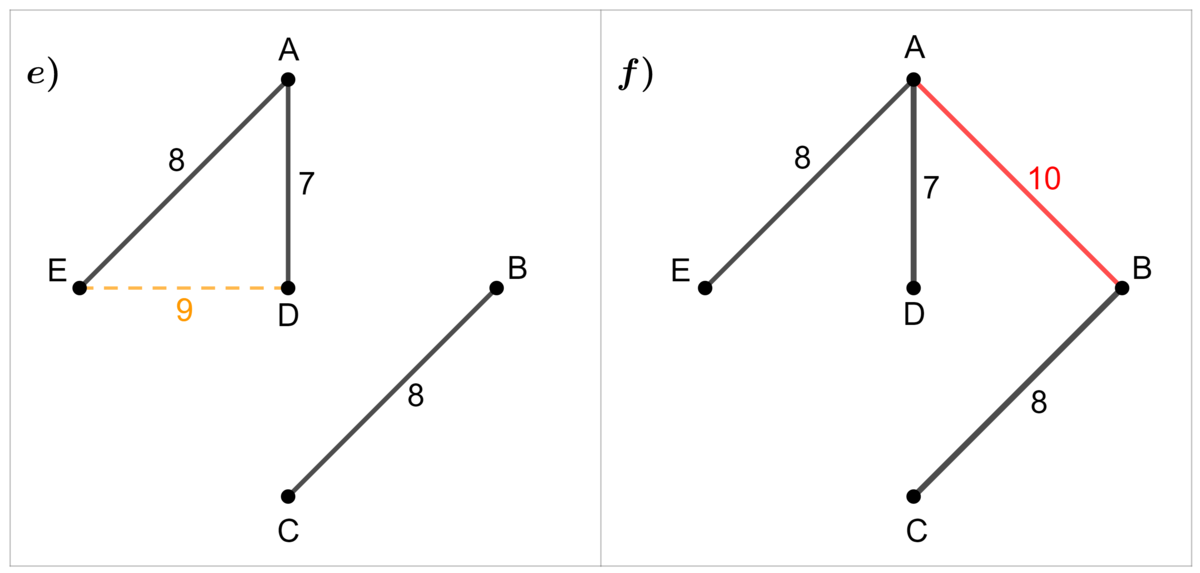
Since the edge |\overline{ED}| would create a simple circuit, we move on to the next.
After selecting the edge |\overline{AB}|, all vertices are now connected. Therefore we have the tree of minimum value.
Step 4
Calculate the weight of the resulting tree.
We need to add all the values of the selected edges to know the total cost of the work.
|\text{Cost}=7+8+8+10=33 \text{ thousand dollars}=33\ 000| $