
The unit circle is a circle with a centre corresponding to the origin of the Cartesian plane |(0,0)| and a radius measuring |1| unit:
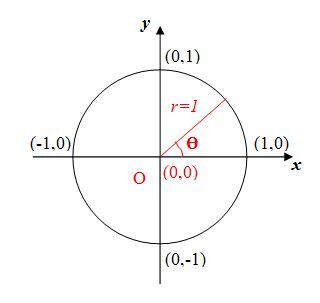
The equation of the circle with Cartesian coordinates is |x^2+y^2=1|.
Several concepts are related to the unit circle and its application in certain contexts:
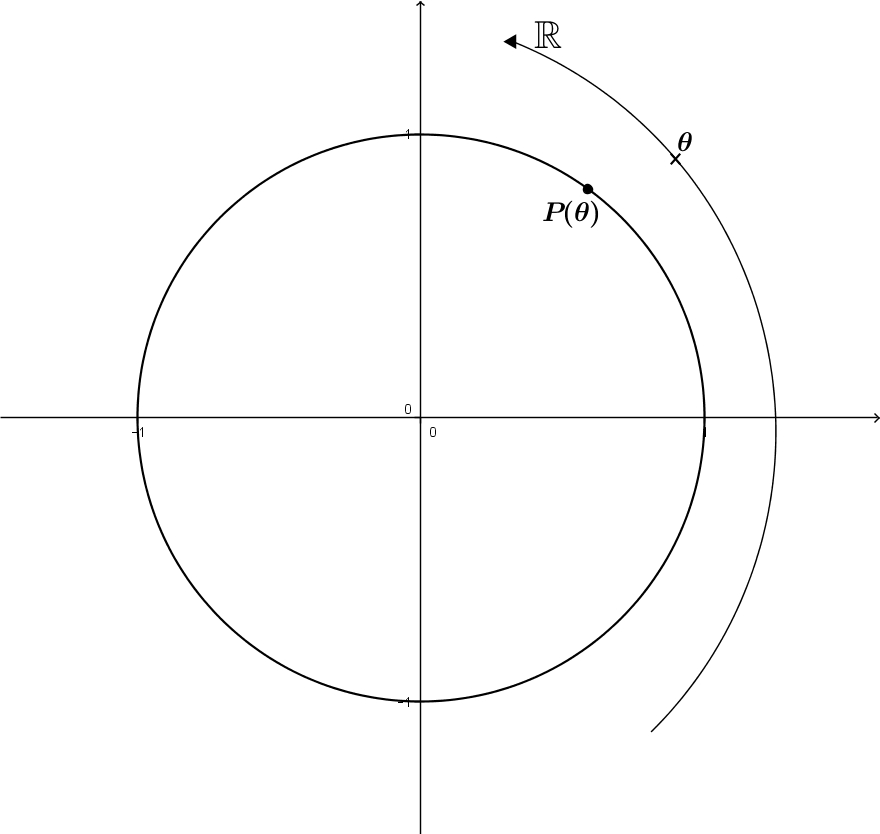
When measuring an angle in the unit circle, always start from the point |(1, 0).|
To find the coordinates of other points on the unit circle, it suffices to know the angle measurement at the centre and to apply the Pythagorean theorem in a right triangle with a hypotenuse of 1 unit.
|
Since the sum of the interior angles of a triangle is 180°, when one angle in a right triangle measures 45°, the other angle also measures 45°. Thus, we have a right-angled isosceles triangle: ||\begin{align} x^{2} + y^{2} &= r^{2} \\ x^{2} + y^{2} &= 1^2 \\ x^{2} + x^{2} &= 1 \\ 2x^{2} &= 1 \\ x^{2} &= \frac{1}{2} \\ x &= \sqrt{\frac{1}{2}} \\ x &= \frac{1}{\sqrt{2}} \\ x &= \frac{1}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ &(\text{Rationalization}) \\ x &= \frac{\sqrt{2}}{2} \end{align}|| In an isosceles triangle, both sides have the same measurement. ||y=\frac{\sqrt{2}}{2}|| |
In a right triangle with an angle of 30°, the side measure opposite the 30° angle is equal to half the hypotenuse’s measurement. Thus, since the hypotenuse is the radius and the radius is 1: |y=\dfrac{1}{2}| ||\begin{align} x^{2} + y^{2} &= r^{2} \\ x^{2} + \left(\frac{1}{2}\right)^{2} &= 1^2 \\ x^{2} + \frac{1}{4} &= 1 \\ x^{2} &= 1 - \frac{1}{4} \\ x^{2} &=\frac{3}{4} \\ x &= \sqrt{\frac{3}{4}} \\\\ x &= \frac{\sqrt{3}}{2} \end{align}|| |
|
Therefore, the coordinates of the point are: |\displaystyle P\left(\frac{\pi}{4}\right)=\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)| |
Therefore, the coordinates of the point are: |\displaystyle P\left(\frac{\pi}{6}\right)=\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)| |
From this information, here are the coordinates of some points on the unit circle that are associated with certain remarkable angles.

-
Each point is called a trigonometric point |P(\theta)| where |\theta| is the measure of an angle in radians. In short, a trigonometric point is a point on the unit circle.
-
The coordinates |(x,y)| of each of the points represent |\cos \theta| and |\sin \theta|, respectively. ||P(\theta)=(x,y)= (\cos \theta,\sin \theta)||
-
Therefore, the unit circle’s equation |x^2+y^2=1| becomes: ||\cos^2 \theta + \sin^2 \theta=1||
Notice the arrangement of the main trigonometric points on the unit circle. When the points of the Cartesian plane’s first quadrant are learnt, the other points can be obtained by carrying out a reflection in relation to the axes. Then, only the signs of the coordinates change.
For example, a point |(x,y)| of the first quadrant becomes |(-x,y)| in the second quadrant.
Therefore, it is not necessary to memorize the entire unit circle. You only have to learn the first quadrant.
|
Degrees |(°)| |
Radians |(\text{rad})| |
|x=\cos \theta| |
|y=\sin \theta| |
|\begin{align} P(\theta) &=(x,y) \\ &= (\cos \theta, \sin \theta) \end{align}| |
|---|---|---|---|---|
|
|0°| |
|0| |
|1| |
|0| |
|(1,0)| |
|
|30°| |
|\dfrac{\pi}{6}| |
|\dfrac{\sqrt{3}}{2}| |
|\dfrac{1}{2}| |
|\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)| |
|
|45°| |
|\dfrac{\pi}{4}| |
|\dfrac{\sqrt{2}}{2}| |
|\dfrac{\sqrt{2}}{2}| |
|\left(\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)| |
|
|60°| |
|\dfrac{\pi}{3}| |
|\dfrac{1}{2}| |
|\dfrac{\sqrt{3}}{2}| |
|\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)| |
|
|90°| |
|\dfrac{\pi}{2}| |
|0| |
|1| |
|(0,1)| |
|
|120°| |
|\dfrac{2\pi}{3}| |
|-\dfrac{1}{2}| |
|\dfrac{\sqrt{3}}{2}| |
|\left(-\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)| |
|
|135°| |
|\dfrac{3\pi}{4}| |
|-\dfrac{\sqrt{2}}{2}| |
|\dfrac{\sqrt{2}}{2}| |
|\left(-\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)| |
|
|150°| |
|\dfrac{5\pi}{6}| |
|-\dfrac{\sqrt{3}}{2}| |
|\dfrac{1}{2}| |
|\left(-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)| |
|
|180°| |
|\pi| |
|-1| |
|0| |
|(-1,0)| |
|
|210°| |
|\dfrac{7\pi}{6}| |
|-\dfrac{\sqrt{3}}{2}| |
|-\dfrac{1}{2}| |
|\left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)| |
|
|225°| |
|\dfrac{5\pi}{4}| |
|-\dfrac{\sqrt{2}}{2}| |
|-\dfrac{\sqrt{2}}{2}| |
|\left(-\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)| |
|
|240°| |
|\dfrac{4\pi}{3}| |
|-\dfrac{1}{2}| |
|-\dfrac{\sqrt{3}}{2}| |
|\left(-\dfrac{1}{2},-\dfrac{\sqrt{3}}{2}\right)| |
|
|270°| |
|\dfrac{3\pi}{2}| |
|0| |
|-1| |
|(0,-1)| |
|
|300°| |
|\dfrac{5\pi}{3}| |
|\dfrac{1}{2}| |
|-\dfrac{\sqrt{3}}{2}| |
|\left(\dfrac{1}{2},-\dfrac{\sqrt{3}}{2}\right)| |
|
|315°| |
|\dfrac{7\pi}{4}| |
|\dfrac{\sqrt{2}}{2}| |
|-\dfrac{\sqrt{2}}{2}| |
|\left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)| |
|
|330°| |
|\dfrac{11\pi}{6}| |
|\dfrac{\sqrt{3}}{2}| |
|-\dfrac{1}{2}| |
|\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)| |
|
|360°| |
|2\pi| |
|1| |
|0| |
|(1,0)| |
We generally use radians rather than degrees when working with the unit circle.
Knowing the main points of the unit circle is not enough. It is also necessary to be able to determine if a given point is on the unit circle.
When the Cartesian coordinates of the point are known, check whether the equation |x^2+y^2=1| is respected. If not, the given point is not on the unit circle.
Is the point |(0.6,0.8)| on the unit circle?
Replace |x| and |y| in |x^2+y^2=1| by the values of the point. ||0.6^2+0.8^2=0.36+0.64=1||
Therefore, the point |(0.6,0.8)| is on the unit circle.
Is the point |\left(\dfrac{1}{4}, \dfrac{2}{3}\right)| on the unit circle?
Replace |x| and |y| in |x^2+y^2=1| by the values of the point. ||\left(\dfrac{1}{4}\right)^2 + \left(\dfrac{2}{3}\right)^2 = \dfrac{1}{16} + \dfrac{4}{9} = \dfrac{73}{144} \neq 1||
Therefore, the point |\left(\dfrac{1}{4}, \dfrac{2}{3}\right)| is not on the unit circle.
A cyclical function associates a point |P(\theta)| on the unit circle centred in |(0,0)| with any real number |\theta| on the real number line. It is a function |f| such that |\begin{eqnarray*}f: \mathbb{R} &\to& [-1,1] \times [-1,1] \\ \theta &\mapsto & (\cos \theta, \sin \theta) \end{eqnarray*}.|
Here are some diagrams:
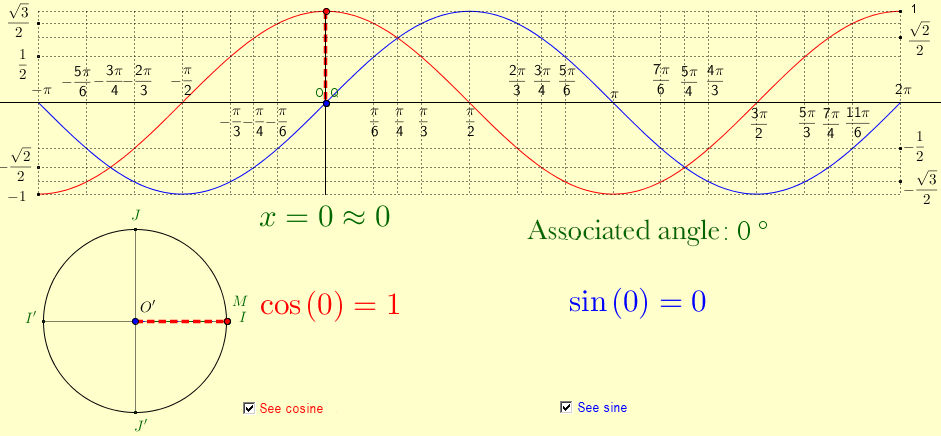
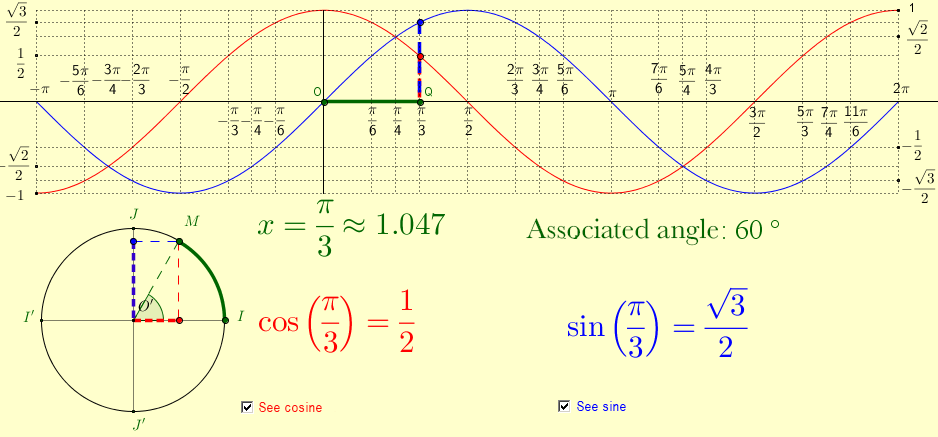
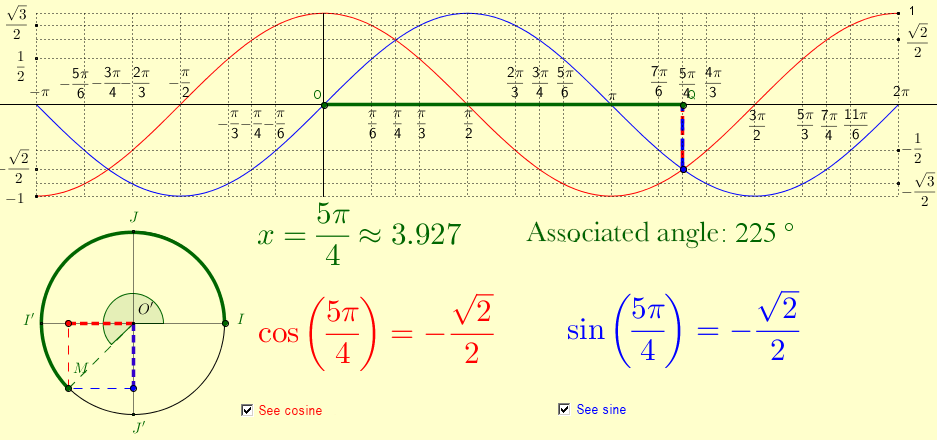
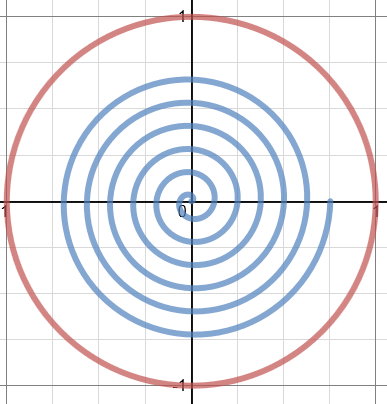
It means that, regardless of the value of |\theta|, it is always possible to associate a point |(x,y)=(\cos \theta, \sin \theta)| located on the unit circle. It can be said that the real number line wraps around the trigonometric circle. Notice that the real number line in the image on the right wraps around the circle in comparison to the image on the left.
The trigonometric points are periodic. No matter how many turns you make around the circle, it is always possible to get back to the interval |[0,2\pi].|
A period is the smallest positive real number |p|, such as |P(\theta + p) = P(\theta).|
In terms of trigonometric points, the period is |2\pi| radians.
Different formulas can be established. Here are two of them:
|\bullet| |\cos(\theta + 2\pi n) = \cos \theta|
|\bullet| |\sin(\theta + 2\pi n) = \sin \theta|
The two formulas are valid regardless of the value of |\theta|. In addition, the values of |n| must be integers.
For example, take the trigonometric point |P(\theta) = \left(\dfrac{5}{13},\dfrac{12}{13}\right).|
We want to know the value of the point when the angle is |\theta + 8 \pi| radians.
Note that |8\pi| is a multiple of |2\pi|. Indeed, |4 \times 2\pi = 8\pi.| Thus, |n=4.|
Apply the two formulas shown above:
-
|\cos(\theta + 8\pi) = \cos \theta = \dfrac{5}{13}|
-
|\sin(\theta + 8\pi) = \sin \theta = \dfrac{12}{13}|
This gives the same point |P(\theta + 8\pi) = \left(\dfrac{5}{13},\dfrac{12}{13}\right).|
To find the coordinates of a point when the angle measurement is not in the interval |[0,2\pi]| radians, subtract the angle corresponding to the number of complete rotations it contains from the given angle. Thus, the result will be brought back to the interval |[0,2\pi].|
Here are the steps in more detail:
-
Calculate the number of rotations |N| to be subtracted from the given angle |t| by dividing the angle measurement by |2\pi| and rounding the result obtained down to the nearest integer:
|\displaystyle N=\left[\frac{t}{2\pi}\right]| -
Subtract the angle formed by the number of rotations previously calculated from the given angle (thus, the measurement is |2\pi N|): |t'=t-2\pi N|
-
Locate the result of the previous subtraction, which is a number between |0| and |2\pi,| on the unit circle and indicate its coordinates.
BE CAREFUL: When the angle has a negative value, the value of |N| will also be negative. In this case, subtract a negative multiple of |2\pi,| which amounts to adding rotations to find the result in the interval |[0,2\pi].|
Determine the position of the point on the unit circle |P(\frac{31\pi}{6})| and indicate its coordinates.
-
Calculate the number of rotations
|\displaystyle N= \left[t\div2\pi\right]|
|\displaystyle N=\left[\frac{31\pi}{6}\div2\pi \right]|
|N=[2{.}583...]|
|N=2| -
Subtract the number of rotations
|t'=t-N\times2\pi|
|t'=\frac{31\pi}{6}-2\times2\pi|
|t'=\frac{31\pi}{6} -\frac{24\pi}{6}|
|t'=\frac{7\pi}{6}| -
Locate the point
The point coincides with the point |P(\frac{7\pi}{6}) = (-\frac{\sqrt{3}}{2},-\frac{1}{2})| so its coordinates are: ||P\left(\frac{31\pi}{6}\right)=\left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right)||
Determine the position of the point on the unit circle |P(\frac{-26\pi}{3})| and indicate its coordinates.
-
Calculate the number of rotations
|N=[t\div2\pi]|
|\displaystyle N= \left[\frac{-26\pi}{3}\div2\pi \right]|
|N=[-4{,}33...]|
|N=-5| -
Subtract the number of rotations
|t'=t-N\times2\pi|
|t'=\dfrac{-26\pi}{3}-(-5)\times2\pi|
|t'=\dfrac{-26\pi}{3} -(-10\pi)|
|t'=\dfrac{4\pi}{3}| -
Locate the point
The point coincides with the point |P(\frac{4\pi}{3})=(-\frac{1}{2},-\frac{\sqrt{3}}{2})| so its coordinates are: ||P\left(\frac{-26\pi}{3}\right)=\left(-\frac{1}{2},-\frac{\sqrt{3}}{2}\right)||
We may also want to find the opposite, i.e., we may want to find the value of an angle in a given interval |[a,b]| if we know its coordinates.
To find the value of an angle, first identify the angle measurement from its coordinates in the interval |[0,2\pi],| and add the number of rotations necessary to obtain the angle included in the requested interval.
Here are the steps in more detail:
-
On the unit circle, locate the point whose coordinates are known and find the value of |t’| associated with the point in the interval |[0,2\pi].|
-
Calculate the number of rotations to add to |t’| using the formula |\displaystyle N=\left[\frac{b-t'}{2\pi}\right]|, where the square brackets denote rounding down to the nearest integer and where |b| represents the upper boundary of the requested interval.
-
Add to |t’| the number of rotations calculated previously using the formula: |t=t' + 2\pi N|
Determine the value of the angle |t| in radians if |P(t) = \left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)| and if |t \in [9\pi,11\pi].|
-
Location of the point on the unit circle
Between |0| and |2\pi|, the angle at the centre corresponding to the point with coordinates |\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)| is |\frac{7\pi}{4}.|
Note the point |t’.| -
Calculation of the number of rotations
|\displaystyle N=\left[\frac{b-t'}{2\pi}\right]|
|\displaystyle N=\left[\frac{11\pi-\frac{7\pi}{4}}{2\pi}\right]|
|\displaystyle N=\left[\frac{\frac{37\pi}{4}}{2\pi}\right]|
|\displaystyle N=\left[\frac{37}{8}\right]|
|N=[4{.}625]|
|N=4| -
Add the number of rotations
|t=t'+N\times2\pi|
|t=\dfrac{7\pi}{4}+4\times2\pi|
|t=\dfrac{7\pi}{4}+8\pi|
|t=\dfrac{39\pi}{4}|
In the interval |[9\pi,11\pi]| , the point |P\left(\dfrac{39\pi}{4}\right)| has the coordinates |\left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right).|
Determine the value of the angle |t| in radians if |P(t)=(\frac{\sqrt{3}}{2},\frac{1}{2})| and if |t \in [-6\pi,-4\pi].|
-
Location of the point on the unit circle
Between |0| and |2\pi|, the central angle corresponding to the point with coordinates |(\frac{\sqrt{3}}{2},\frac{1}{2})| is |\dfrac{\pi}{6}.| Note the point |t'.| -
Calculation of the number of rotations
|\displaystyle N=\left[\frac{b-t'}{2\pi}\right]|
|\displaystyle N=\left[\frac{-4\pi-\frac{\pi}{6}}{2\pi} \right]|
|\displaystyle N=\left[\frac{\frac{-25\pi}{6}}{2\pi}\right]|
|\displaystyle N=\left[\frac{-25}{12} \right]|
|N=[-2{.}083...]|
|N=-3| -
Add the number of rotations
|t=t'+N\times2\pi|
|t=\dfrac{\pi}{6}+-3\times2\pi|
|t=\dfrac{\pi}{6}-6\pi|
|t=\dfrac{-35\pi}{6}|
In the interval |[-6\pi,-4\pi]|, the point |P\left(\dfrac{-35\pi}{6}\right)| has the coordinates |\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right).|