Le cercle trigonométrique (aussi appelé le cercle unité) est le cercle dont le centre correspond à l’origine du plan cartésien |(0,0)| et dont le rayon mesure |1| unité :
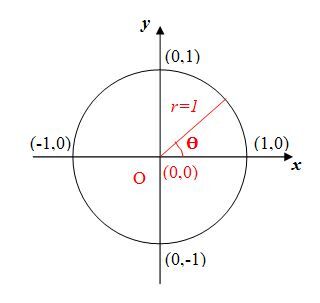
L'équation de ce cercle en coordonnées cartésiennes est |x^2+y^2=1|.
Plusieurs concepts sont reliés au cercle trigonométrique ou à son application dans des contextes donnés :
Lorsqu’on mesure un angle dans le cercle trigonométrique, on part toujours du point |(1, 0).|
Pour trouver les coordonnées d'autres points sur le cercle trigonométrique, il suffit de connaitre la mesure de l'angle au centre et d'appliquer la relation de Pythagore dans un triangle rectangle ayant une hypoténuse de 1 unité.
|
Dans un triangle rectangle dont l'un des angles mesure 45°, l'autre angle mesure 45° aussi puisque la somme des angles intérieurs de tout triangle est 180°. Nous avons donc un triangle rectangle-isocèle : ||\begin{align} x^{2} + y^{2} &= r^{2} \\ x^{2} + y^{2} &= 1^2 \\ x^{2} + x^{2} &= 1 \\ 2x^{2} &= 1 \\ x^{2} &= \frac{1}{2} \\ x &= \sqrt{\frac{1}{2}} \\ x &= \frac{1}{\sqrt{2}} \\ x &= \frac{1}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ &(\text{rationnalisation}) \\ x &= \frac{\sqrt{2}}{2} \end{align}|| Dans un triangle isocèle, les deux côtés du triangle ont la même mesure. ||y=\frac{\sqrt{2}}{2}|| |
Dans un triangle rectangle comportant un angle de 30°, la mesure du côté opposé à l’angle de 30° est égale à la demi-mesure de l’hypoténuse. Ainsi, comme l'hypoténuse est le rayon et que le rayon mesure 1 : |y=\dfrac{1}{2}| ||\begin{align} x^{2} + y^{2} &= r^{2} \\ x^{2} + \left(\frac{1}{2}\right)^{2} &= 1^2 \\ x^{2} + \frac{1}{4} &= 1 \\ x^{2} &= 1 - \frac{1}{4} \\ x^{2} &=\frac{3}{4} \\ x &= \sqrt{\frac{3}{4}} \\\\ x &= \frac{\sqrt{3}}{2} \end{align}|| |
|
Les coordonnées du point sont donc : |\displaystyle P\left(\frac{\pi}{4}\right)=\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)| |
Les coordonnées du point sont donc : |\displaystyle P\left(\frac{\pi}{6}\right)=\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)| |
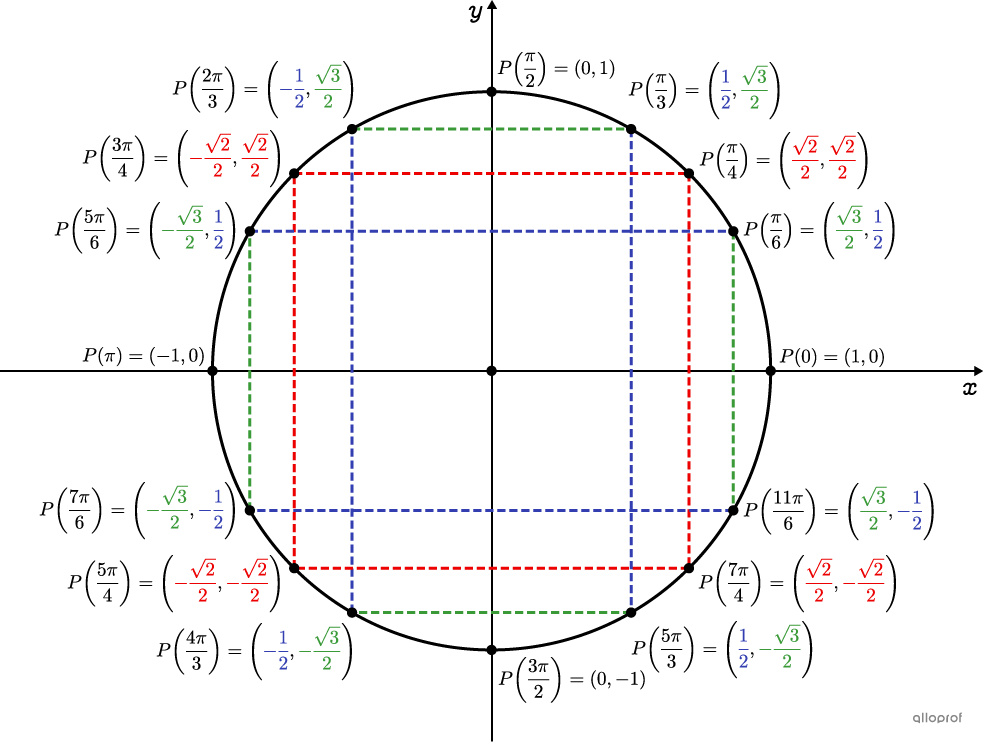
À partir de ces informations, voici les coordonnées de quelques points du cercle trigonométrique associées à certains angles remarquables.
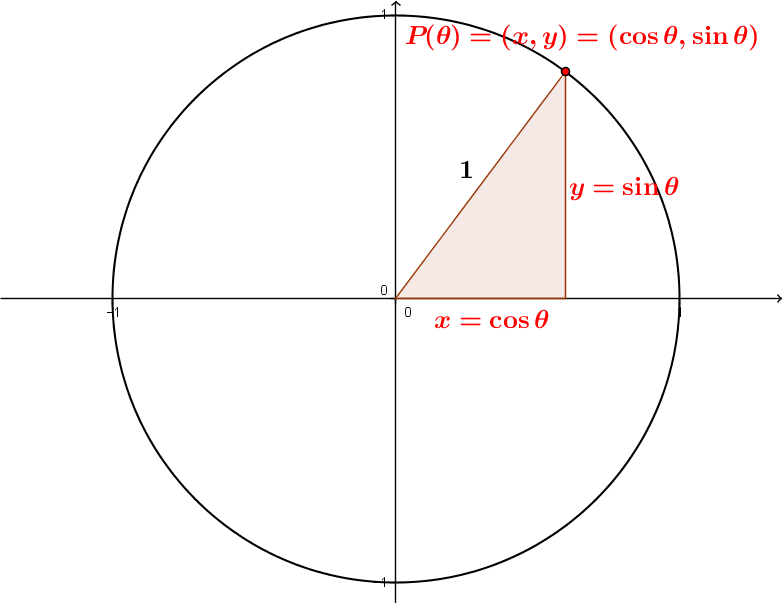
-
Chacun de ces points est appelé point trigonométrique |P(\theta)| où |\theta| est la mesure d'un angle en radians. En bref, un point trigonométrique est un point situé sur le cercle trigonométrique.
-
Les coordonnées |(x,y)| de chacun de ces points représentent respectivement |\cos \theta| et |\sin \theta|. ||P(\theta)=(x,y)= (\cos \theta,\sin \theta)||
-
L'équation du cercle trigonométrique |x^2+y^2=1| devient donc : ||\cos^2 \theta + \sin^2 \theta=1||
Il est intéressant de remarquer l'agencement des points trigonométriques remarquables comme on peut le voir sur le cercle trigonométrique. En effet, lorsqu'on connait les points du premier quadrant du plan cartésien, on obtient les autres points en effectuant des réflexions par rapport aux axes. Il n'y a alors que les signes des coordonnées qui changent.
Par exemple, un point |(x,y)| du premier quadrant deviendra |(-x,y)| dans le second quadrant.
Il n'est donc pas nécessaire de mémoriser en entier le cercle trigonométrique. Il faut seulement apprendre le premier quadrant.
|
Degrés |(°)| |
Radians |(\text{rad})| |
|x=\cos \theta| |
|y=\sin \theta| |
|\begin{align} P(\theta) &=(x,y) \\ &= (\cos \theta, \sin \theta) \end{align}| |
|---|---|---|---|---|
| |0°| | |0| | |1| | |0| | |(1,0)| |
| |30°| | |\dfrac{\pi}{6}| | |\dfrac{\sqrt{3}}{2}| | |\dfrac{1}{2}| | |\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)| |
| |45°| | |\dfrac{\pi}{4}| | |\dfrac{\sqrt{2}}{2}| | |\dfrac{\sqrt{2}}{2}| | |\left(\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)| |
| |60°| | |\dfrac{\pi}{3}| | |\dfrac{1}{2}| | |\dfrac{\sqrt{3}}{2}| | |\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)| |
| |90°| | |\dfrac{\pi}{2}| | |0| | |1| | |(0,1)| |
| |120°| | |\dfrac{2\pi}{3}| | |-\dfrac{1}{2}| | |\dfrac{\sqrt{3}}{2}| | |\left(-\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)| |
| |135°| | |\dfrac{3\pi}{4}| | |-\dfrac{\sqrt{2}}{2}| | |\dfrac{\sqrt{2}}{2}| | |\left(-\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)| |
| |150°| | |\dfrac{5\pi}{6}| | |-\dfrac{\sqrt{3}}{2}| | |\dfrac{1}{2}| | |\left(-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)| |
| |180°| | |\pi| | |-1| | |0| | |(-1,0)| |
| |210°| | |\dfrac{7\pi}{6}| | |-\dfrac{\sqrt{3}}{2}| | |-\dfrac{1}{2}| | |\left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)| |
| |225°| | |\dfrac{5\pi}{4}| | |-\dfrac{\sqrt{2}}{2}| | |-\dfrac{\sqrt{2}}{2}| | |\left(-\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)| |
| |240°| | |\dfrac{4\pi}{3}| | |-\dfrac{1}{2}| | |-\dfrac{\sqrt{3}}{2}| | |\left(-\dfrac{1}{2},-\dfrac{\sqrt{3}}{2}\right)| |
| |270°| | |\dfrac{3\pi}{2}| | |0| | |-1| | |(0,-1)| |
| |300°| | |\dfrac{5\pi}{3}| | |\dfrac{1}{2}| | |-\dfrac{\sqrt{3}}{2}| | |\left(\dfrac{1}{2},-\dfrac{\sqrt{3}}{2}\right)| |
| |315°| | |\dfrac{7\pi}{4}| | |\dfrac{\sqrt{2}}{2}| | |-\dfrac{\sqrt{2}}{2}| | |\left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)| |
| |330°| | |\dfrac{11\pi}{6}| | |\dfrac{\sqrt{3}}{2}| | |-\dfrac{1}{2}| | |\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)| |
| |360°| | |2\pi| | |1| | |0| | |(1,0)| |
Lorsqu'on travaille avec le cercle trigonométrique, on utilise généralement les radians plutôt que les degrés.
Ce n'est pas tout de connaitre les points remarquables du cercle trigonométrique. Il faut également pouvoir déterminer si un point donné est sur le cercle trigonométrique.
Lorsqu'on connait les coordonnées cartésiennes du point, il faut vérifier si la relation |x^2+y^2=1| est respectée. Si ce n'est pas le cas, le point donné n'est pas sur le cercle trigonométrique.
Le point |(0{,}6\ ;\ 0{,}8)| est-il sur le cercle trigonométrique?
On remplace |x| et |y| dans |x^2+y^2=1| par les valeurs du point donné. ||0{,}6^2 + 0{,}8^2 = 0{,}36 + 0{,}64 = 1||
On peut donc affirmer que le point |(0{,}6\ ;\ 0{,}8)| est sur le cercle trigonométrique.
Le point |\left(\dfrac{1}{4}, \dfrac{2}{3}\right)| est-il sur le cercle trigonométrique?
On remplace |x| et |y| dans |x^2+y^2=1| par les valeurs du point donné. ||\left(\dfrac{1}{4}\right)^2 + \left(\dfrac{2}{3}\right)^2 = \dfrac{1}{16} + \dfrac{4}{9} = \dfrac{73}{144} \neq 1||
Ainsi, le point |\left(\dfrac{1}{4}, \dfrac{2}{3}\right)| n'est pas sur le cercle trigonométrique.
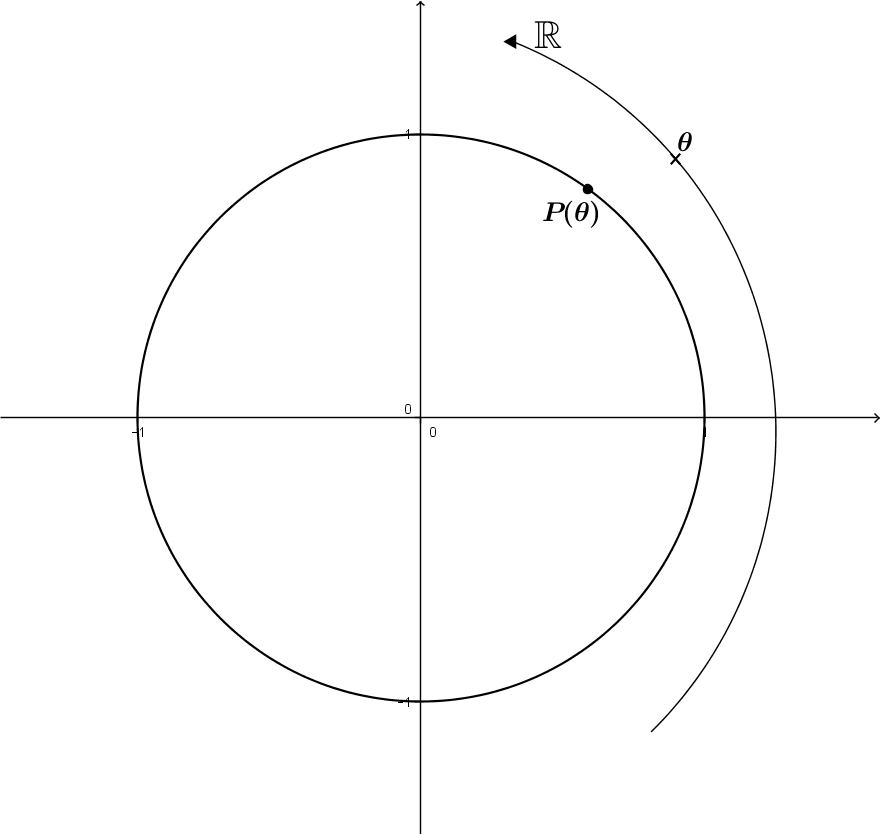
On appelle fonction d'enroulement une fonction qui, à tout nombre réel |\theta| de la droite réelle, associe un point |P(\theta)| sur le cercle trigonométrique centré en |(0,0)|. C'est donc une fonction |f| telle que |\begin{eqnarray*}f: \mathbb{R} &\to& [-1,1] \times [-1,1] \\ \theta &\mapsto & (\cos \theta, \sin \theta) \end{eqnarray*}.|
Voici quelques schémas :
C'est donc dire que, peu importe la valeur de |\theta|, il est toujours possible de lui associer un point |(x,y)=(\cos \theta, \sin \theta)| situé sur le cercle trigonométrique. On dit alors que la droite réelle s'enroule autour du cercle trigonométrique. Dans l'image de gauche, on aperçoit la droite réelle et dans l'image de droite cette dernière s'enroule autour du cercle.
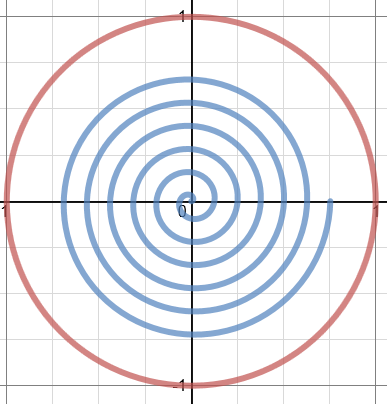
Les points trigonométriques sont périodiques, c'est-à-dire que, peu importe le nombre de tours qu'on effectue autour du cercle, il est toujours possible de se ramener dans l'intervalle |[0,2\pi].|
On appelle période le plus petit nombre réel positif |p| tel que |P(\theta + p) = P(\theta).|
Dans le cas des points trigonométriques, la période est de |2\pi| radians.
Il est possible d'établir différentes formules, en voici deux :
|\cos(\theta + 2\pi n) = \cos \theta|
|\sin(\theta + 2\pi n) = \sin \theta|
Ces deux formules sont valides peu importe la valeur de |\theta.| De plus, les valeurs de |n| doivent être entières.
Soit le point trigonométrique |P(\theta) = \left(\dfrac{5}{13},\dfrac{12}{13}\right).|
On veut savoir la valeur du point lorsque l'angle est plutôt |\theta + 8 \pi| radians.
On remarque que |8\pi| est un multiple de |2\pi|. En effet, |4 \times 2\pi = 8\pi.| Donc, |n=4.|
On peut donc appliquer les deux formules vues plus haut :
-
|\cos(\theta + 8\pi) = \cos \theta = \dfrac{5}{13}|
-
|\sin(\theta + 8\pi) = \sin \theta = \dfrac{12}{13}|
On obtient le même point |P(\theta + 8\pi) = \left(\dfrac{5}{13},\dfrac{12}{13}\right).|
Pour trouver les coordonnées d’un point lorsque la mesure de l’angle n'est pas dans l'intervalle |[0,2\pi]| rad, il faut retrancher de l’angle donné l’angle correspondant au nombre de rotations complètes qu’il contient. Le résultat sera ainsi ramené dans l’intervalle |[0,2\pi].|
Voici plus en détail les étapes à suivre :
-
Calculer le nombre de rotations |N| à retrancher de l’angle donné |t| en divisant cette mesure d’angle par |2\pi| et en conservant la partie entière du résultat obtenu :
|\displaystyle N=\left[\frac{t}{2\pi}\right]|
-
Soustraire de l’angle donné l’angle formé par le nombre de rotations précédemment calculées (dont la mesure est donc de |2\pi N|) : |t'=t-2\pi N|
-
Situer le résultat de la soustraction précédente, qui est un nombre compris entre |0| et |2\pi,| sur le cercle trigonométrique et indiquer ses coordonnées.
ATTENTION : Lorsque l’angle aura une valeur négative, la valeur de |N| sera elle aussi négative. Donc, il faudra soustraire un multiple négatif de |2\pi|, ce qui reviendra à additionner des rotations pour trouver le résultat dans l’intervalle |[0,2\pi].|
Déterminer la position, sur le cercle trigonométrique, du point |P\left(\dfrac{31\pi}{6}\right)| et indiquer ses coordonnées.
-
Calculer le nombre de rotations ||\begin{align} N&= \left[t\div2\pi\right]\\ &=\left[\dfrac{31\pi}{6}\div2\pi \right]\\ &=[2{,}583...]\\&=2\end{align}||
-
Soustraire le nombre de rotations ||\begin{align} t'&=t-N\times2\pi\\&=\dfrac{31\pi}{6}-2\times2\pi\\&=\dfrac{31\pi}{6} -\dfrac{24\pi}{6}\\&=\frac{7\pi}{6}\end{align}||
-
Localiser le point
Le point coïncide avec le point |P\left(\dfrac{7\pi}{6}\right) = \left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)| de sorte que ses coordonnées sont : ||P\left(\dfrac{31\pi}{6}\right)=\left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)||
Déterminer la position, sur le cercle trigonométrique, du point |P\left(\dfrac{-26\pi}{3}\right)| et indiquer ses coordonnées.
-
Calculer le nombre de rotations ||\begin{align}N&=[t\div2\pi]\\&= \left[\dfrac{-26\pi}{3}\div2\pi \right]\\&=[-4{,}33...]\\&=-5\end{align}||
-
Soustraire le nombre de rotations ||\begin{align}t'&=t-N\times2\pi\\&=\dfrac{-26\pi}{3}-(-5)\times2\pi\\&=\dfrac{-26\pi}{3} -(-10\pi)\\&=\dfrac{4\pi}{3}\end{align}||
-
Localiser le point
Le point coïncide avec le point |P\left(\dfrac{4\pi}{3}\right)=\left(-\dfrac{1}{2},-\dfrac{\sqrt{3}}{2}\right)| de sorte que ses coordonnées sont : ||P\left(\dfrac{-26\pi}{3}\right)=\left(-\dfrac{1}{2},-\dfrac{\sqrt{3}}{2}\right)||
On peut aussi vouloir trouver l’inverse, c’est-à-dire qu’on peut vouloir trouver la valeur d’un angle dans un intervalle donné |[a,b]| en connaissant ses coordonnées.
Pour trouver la valeur d’un angle, on doit d’abord identifier la mesure de l’angle à partir de ses coordonnées dans l’intervalle |[0,2\pi],| puis lui ajouter le nombre de rotations nécessaires afin d’obtenir l’angle compris dans l’intervalle demandé.
Voici plus en détail les étapes à suivre :
-
Localiser, sur le cercle trigonométrique, le point dont on connait les coordonnées et trouver la valeur de |t’| associée à ce point dans l’intervalle |[0,2\pi].|
-
Calculer le nombre de rotations à ajouter à |t’| à l’aide de la formule |\displaystyle N=\left[\frac{b-t'}{2\pi}\right]| où les crochets désignent la partie entière et où |b| représente la seconde borne de l’intervalle demandé.
-
Additionner à |t’| le nombre de rotations calculé précédemment à l’aide de la formule: |t=t' + 2\pi N|
Déterminer la valeur de l'angle |t| en radians si |P(t) = \left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)| et si |t \in [9\pi,11\pi].|
-
Localisation du point sur le cercle trigonométrique
Entre |0| et |2\pi,| l’angle au centre correspondant au point de coordonnées |\left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)| est de |\dfrac{7\pi}{4}.|
On notera ce point |t’.| -
Calcul du nombre de rotations ||\begin{align}N&=\left[\dfrac{b-t'}{2\pi}\right]\\ &=\left[\dfrac{11\pi-\frac{7\pi}{4}}{2\pi}\right]\\ &=\left[\dfrac{\frac{37\pi}{4}}{2\pi}\right]\\ &=\left[\dfrac{37}{8}\right]\\&=[4{,}625]\\&=4\end{align}||
-
Additionner le nombre de rotations ||\begin{align}t&=t'+N\times2\pi\\&=\dfrac{7\pi}{4}+4\times2\pi\\ &=\dfrac{7\pi}{4}+8\pi\\ &=\dfrac{39\pi}{4}\end{align}||Dans l’intervalle |[9\pi,11\pi],| c’est le point |P\left(\dfrac{39\pi}{4}\right)| qui possède les coordonnées |\left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right).|
Déterminer la valeur de l'angle |t| en radians si |P(t)=\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)| et si |t \in [-6\pi,-4\pi].|
-
Localisation du point sur le cercle trigonométrique
Entre |0| et |2\pi,| l’angle au centre correspondant au point de coordonnées |\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)| est de |\dfrac{\pi}{6}.| On notera ce point |t'.| -
Calcul du nombre de rotations ||\begin{align}N&=\left[\dfrac{b-t'}{2\pi}\right]\\ &=\left[\dfrac{-4\pi-\frac{\pi}{6}}{2\pi} \right]\\ &=\left[\dfrac{\frac{-25\pi}{6}}{2\pi}\right]\\ &=\left[\dfrac{-25}{12} \right]\\&=[-2{,}083...]\\&=-3\end{align}||
-
Additionner le nombre de rotations ||\begin{align}t&=t'+N\times2\pi\\&=\dfrac{\pi}{6}+-3\times2\pi\\ &=\dfrac{\pi}{6}-6\pi\\&=\dfrac{-35\pi}{6}\end{align}||Dans l’intervalle |[-6\pi,-4\pi],| c’est le point |P\left(\dfrac{-35\pi}{6}\right)| qui possède les coordonnées |\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right).|