In statistics, graphs are very useful for looking at how data is distributed.
A bar graph is used to represent observed frequencies. It can represent both qualitative data and discrete quantitative data. The characteristics of the bar graph are the following:
-
Each bar is associated with a value and a category.
-
The length of the bar is proportional to its frequency.
-
The distance between each bar must be the same and the first bar must not be directly attached to the parallel axis.
-
The width of the bars should be uniform.
-
The graph should have a title and the axes should be labelled with what they represent.
-
The bars can be vertical or horizontal.
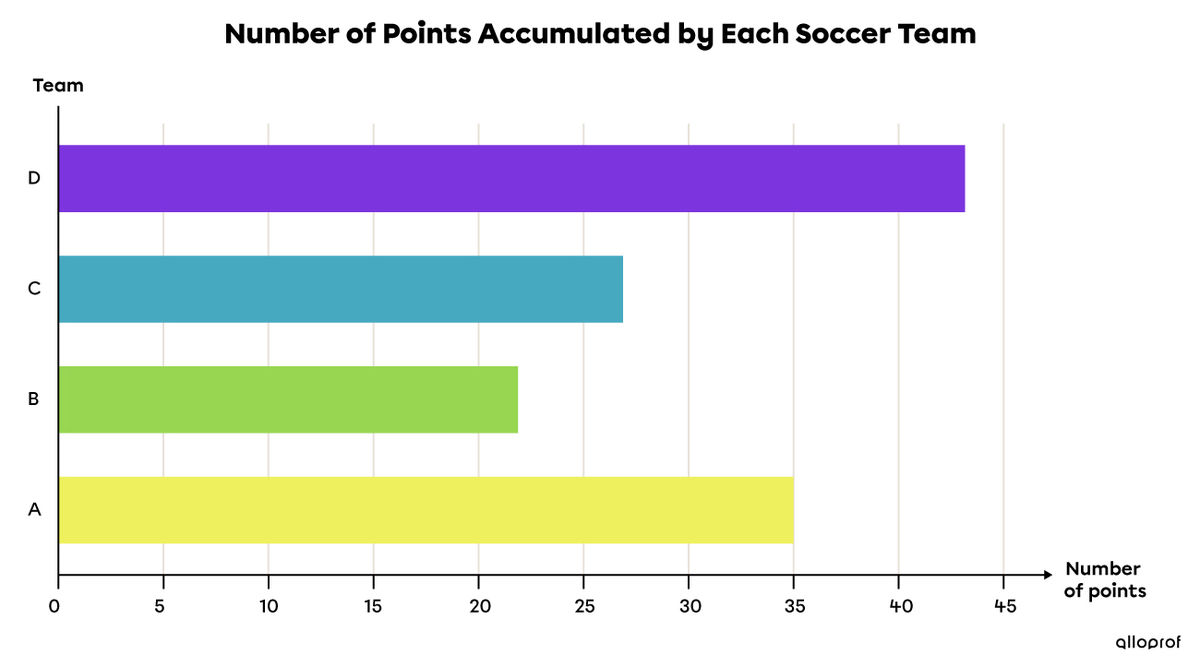
Here is a table of values, along with a horizontal bar graph, representing the number of points accumulated during the soccer season by four different teams.
|
Soccer teams |
A |
B |
C |
D |
|---|---|---|---|---|
|
Number of points accumulated |
|35| |
|22| |
|27| |
|43| |
The same rules must be followed with vertical bar graphs. Essentially, only the orientation of the bars will be different.
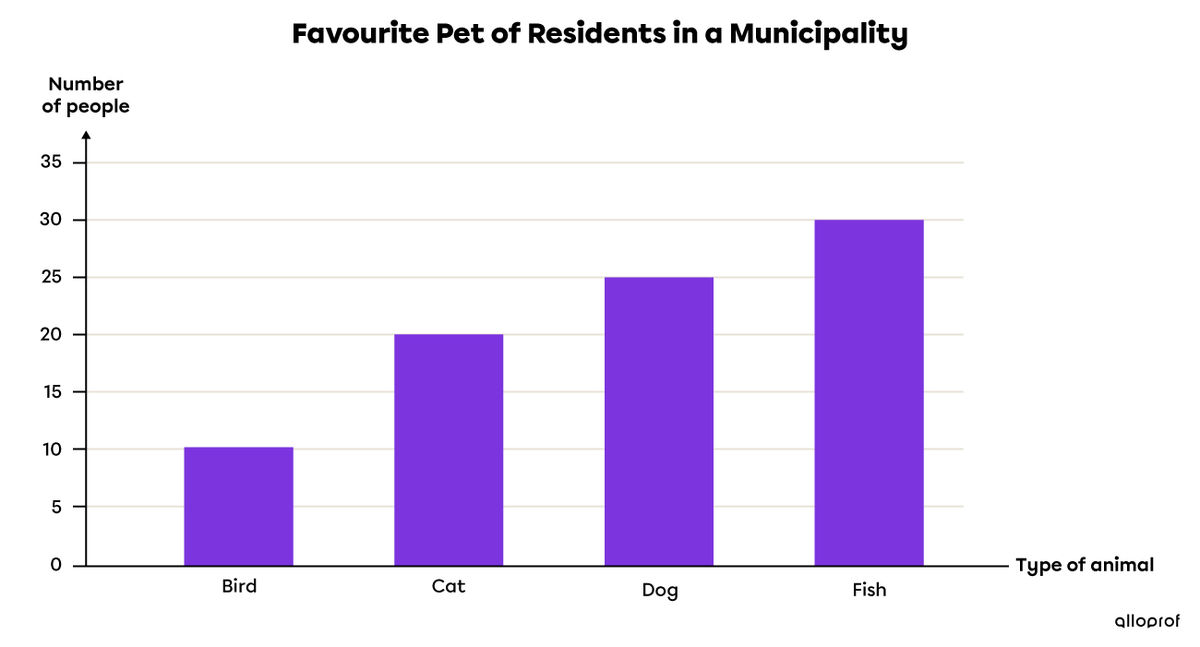
A survey was conducted to determine the favourite pet of the residents in a municipality. Here is a table of values and a vertical bar graph displaying the results.
|
Favourite Pet |
Bird |
Cat |
Dog |
Fish |
|---|---|---|---|---|
|
Number of people |
|10| |
|20| |
|25| |
|30| |
The broken-line graph is used to show discrete quantitative and continuous quantitative data that changes over time. The characteristics of the broken-line graph are the following:
-
Each point is plotted according to the |x|- and |y|-axis.
-
Usually, this kind of graph represents a situation that changes over time (years, months, days, etc.).
-
Starting from the first point, connect each consecutive point using straight lines.
-
The graph must have a title and the axes must be labelled with what they represent.
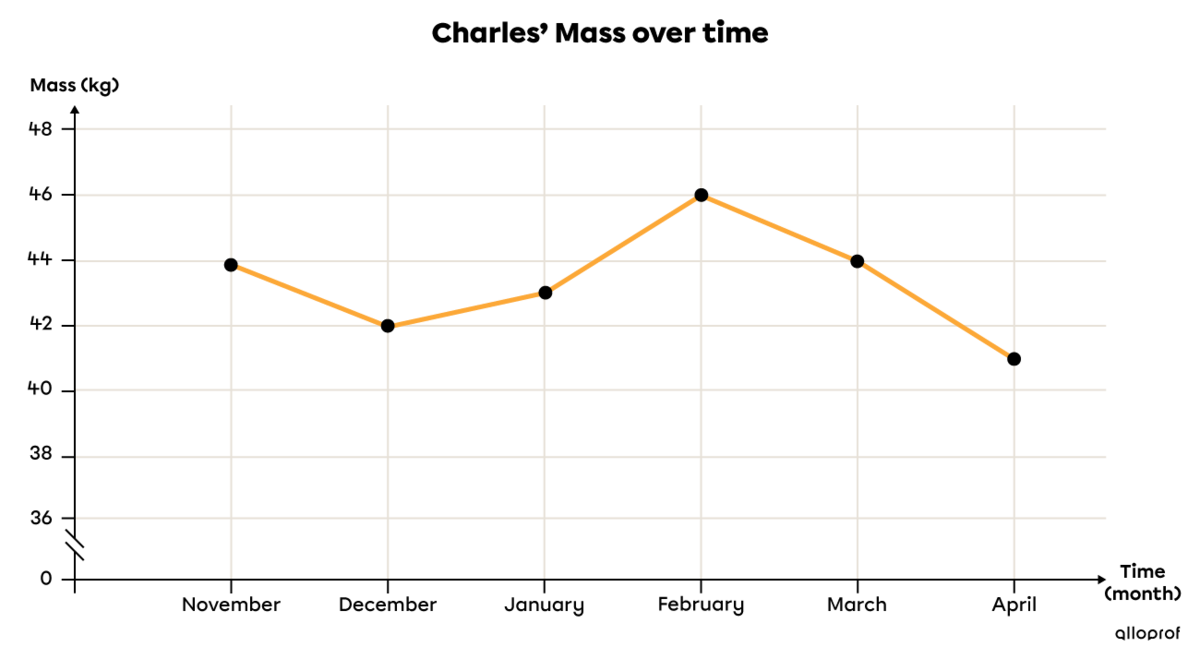
This winter, Charles, a middle school student, experienced serious health problems. His mass fluctuation is shown in a table of values and a broken-line graph.
|
Month |
Nov. |
Dec. |
Jan. |
Feb. |
Mar. |
Apr. |
|---|---|---|---|---|---|---|
|
Mass (kg) |
|44| |
|42| |
|43| |
|46| |
|44| |
|41| |
Frequencies can also be represented in the form of pictographs. In contrast to other diagrams, these consist of drawings that are associated with quantities.
On a beautiful summer evening, Marie and Simon count all the stars they see. Marie sees |65,| while Simon sees |70.| The situation can be represented as follows.
|
Number of stars observed by Marie |
|
|---|---|
|
Number of stars observed by Simon |
|
Legend: each star in the pictograph represents |10| stars.
Interpreting pictographs requires first reading and understanding the legend. In this case, a star represents |10| real stars. From this, it can also be deduced that a half-star represents half of |10| stars, which is |5| stars.
In the pictograph above, there are |6.5| stars, which correspond to the |65| stars observed by Mary.
The pie chart is useful for showing a whole divided into parts. It is used to represent qualitative data. The characteristics of a pie chart are the following:
-
Each circle sector is linked to a category that is usually presented as a percentage.
-
The central angle of each section of the circle represents the proportion of a category with respect to the whole |(360^\circ).|
-
There must be a title and a legend describing the category of each section.
|160| high school students are asked which season is their favourite. Here is the frequency table illustrating the results.
|
Season |
Students |
Relative frequency |(\%)| |
Central angle |(^\circ)| |
|---|---|---|---|
|
Winter |
|48| |
|30| |
|108| |
|
Fall |
|24| |
|15| |
|54| |
|
Spring |
|16| |
|10| |
|36| |
|
Summer |
|72| |
|45| |
|162| |
|
Total |
|160| |
|100| |
|360| |
The relative frequency of a data value can be calculated using the following proportion.||\dfrac{\text{Relative frequency}}{100}=\dfrac{\text{Frequency}}{\text{Total frequency}}||The central angle can be calculated using one of the 2 following proportions.
||\dfrac{\text{Central angle of a section}}{360^\circ}=\dfrac{\text{Frequency}}{\text{Total frequency}}||
||\dfrac{\text{Central angle of a section}}{360^\circ}=\dfrac{\text{Relative frequency}}{100}||
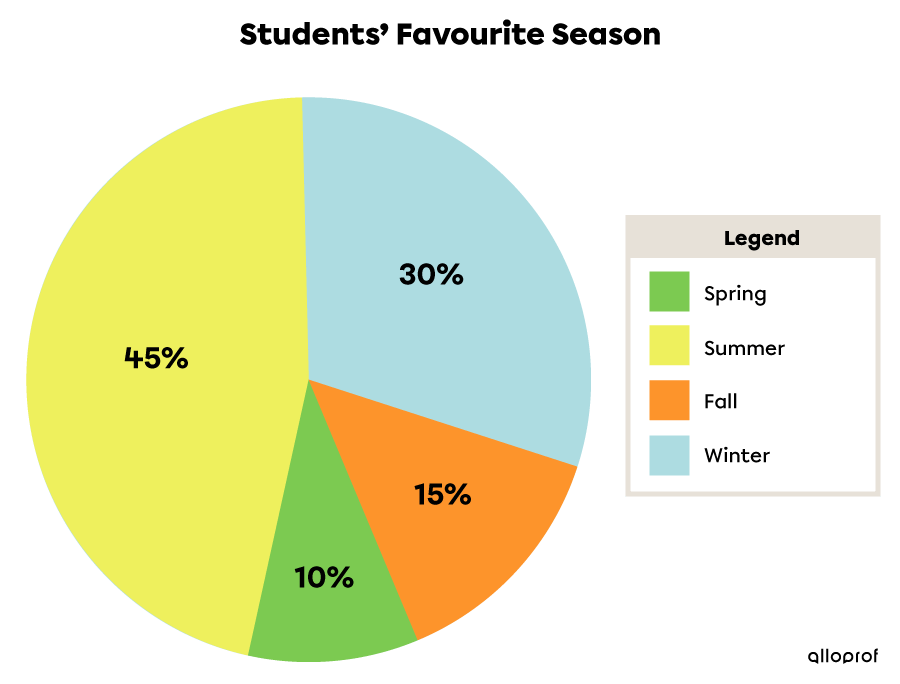
Since the pie chart is made by drawing a circle, we can use certain properties of the circle to find missing quantities.
Here is the incomplete data table of a pie chart.
|
Season |
Students |
Relative frequency |(\%)| |
Central angle |(^\circ)| |
|---|---|---|---|
|
Winter |
|48| |
|30| |
|108| |
|
Fall |
|
|
|
|
Spring |
|16| |
|
|36| |
|
Summer |
|
|45| |
|
|
Total |
|
|100| |
|360| |
To find the value of the green box, use the following proportion.||\begin{align}\dfrac{30}{15}&=\dfrac{108}{\color{#3a9a38}{\text{green box}}}\\\\\color{#3a9a38}{\text{green box}}&=15\times108\div30\\&=54\end{align}||
A histogram is used to represent different frequencies. It can represent discrete quantitative and continuous quantitative data grouped into classes. The characteristics of histograms are the following:
-
The bars are stuck together.
-
The frequency of each value is represented on the vertical axis.
-
The data is grouped into classes, which are labelled on the horizontal axis.
The following histogram represents the number of people who attended a concert, grouped by age.
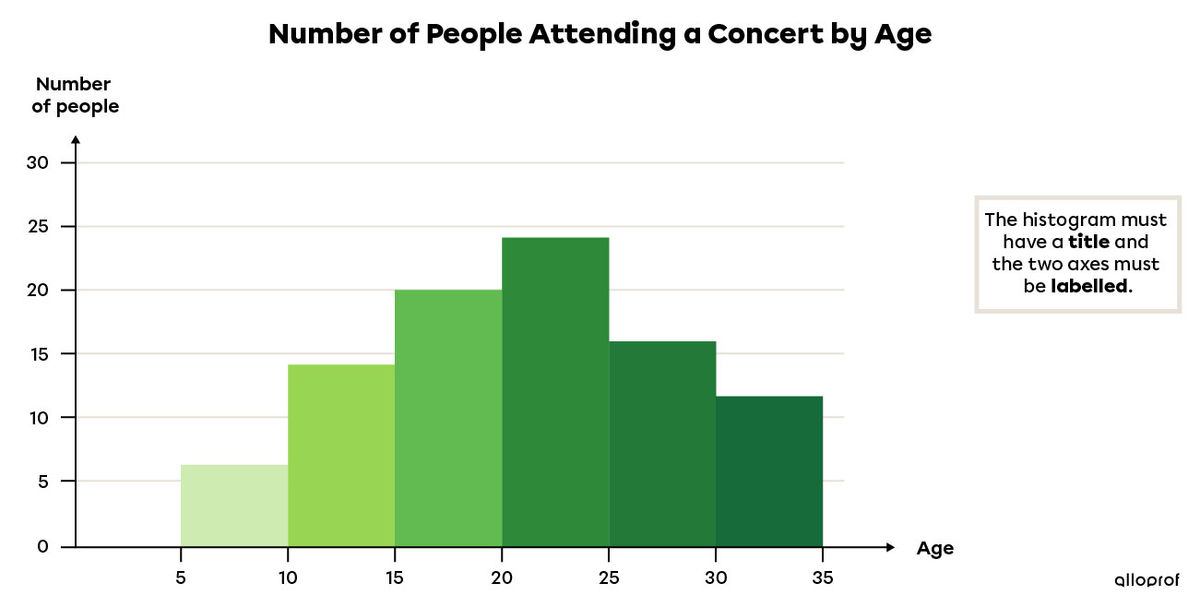
Using this histogram, we can deduce the following distribution table.
|
Age range |
Number of people |
|---|---|
|
|[0,5[| |
|0| |
|
|[5,10[| |
|7| |
|
|[10,15[| |
|14| |
|
|[15,20[| |
|20| |
|
|[20,25[| |
|24| |
|
|[25,30[| |
|16| |
|
|[30,35[| |
|12| |
A stem-and-leaf plot is used to represent different observed frequencies. It can represent discrete quantitative data. The characteristics of the stem-and-leaf plot are the following:
-
Each row is associated with a range of data.
-
Each data value is decomposed into two parts (the stem and the leaf) located on the same line.
To read the stem-and-leaf plot, always associate a number from the stem (centre column) with a number from the leaf (left or right column). The leaves with the smallest numbers are closer to the stem, while those with the largest numbers are further from the stem.
Here is a stem-and-leaf plot that displays the ages of 37 people.
|
Women |
|
Men |
|---|---|---|
|
|6\!-\!5\!-\!2\!-\!2| |
|0| |
|2\!-\!3\!-\!4\!-\!5| |
|
|4\!-\!3\!-\!3\!-\!1| |
|1| |
|0\!-\!0\!-\!1\!-\!6\!-\!8| |
|
|9\!-\!9\!-\!8\!-\!4\!-\!3| |
|2| |
|2\!-\!2\!-\!5\!-\!7\!-\!8| |
|
|9\!-\!8\!-\!7\!-\!6\!-\!5| |
|3| |
|1\!-\!8\!-\!8\!-\!8\!-\!9| |
In this case, the middle column indicates the first number, that is to say, the number in the tens position, of the age of each person. The numbers in the columns on the left (women) and right (men) represent the number found in the ones position of each age.
For example, there are five men in this sample who are in their twenties (number |2| in the centre column). More precisely, the men are |22,| |22,| |25,| |27| and |28| years old.
In the same age group, the five women in this sample are |23,| |24,| |28,| |29| and |29| years old.
On the other hand, it is also possible to construct a stem-and-leaf plot for a distribution of just one group.
On her return from a fishing trip, Gitane noted the length of each of her catches, in millimetres, and here is the list.
|203,| |204,| |206,| |209,| |210,| |212,| |212,| |218,| |226,| |234,| |239,| |240,| |242,| |242,| |242,| |245,| |249,| |250,| |251,| |252,| |257,| |258,| |260,| |262,| |263,| |264|
To simplify her list, she uses a stem and leaf plot. In this case, the stem is composed of the digits of the tens and hundreds position, while the leaves are composed of the ones digits of each data value. She gets the following table.
|
Stem |
Leaf |
|---|---|
|
|20| |
|3\!-\!4\!-\!6\!-\!9| |
|
|21| |
|0\!-\!2\!-\!2\!-\!8| |
|
|22| |
|6| |
|
|23| |
|4\!-\!9| |
|
|24| |
|0\!-\!2\!-\!2\!-\!2\!-\!5\!-\!9| |
|
|25| |
|0\!-\!1\!-\!2\!-\!7\!-\!8| |
|
|26| |
|0\!-\!2\!-\!3\!-\!4| |
