Capacity is a measure of the volume something can hold. For example, the containers below hold a certain quantity of milk and flour.

In everyday life, capacity is used to measure quantities. Among other things, this measurement is very useful in cooking.
The basic unit of capacity, in the International System (SI), is the litre (L).
Here is a table of the most commonly used units:
| Préfixe | kilo- | hecto- | deca- | deci- | centi- | milli- | |
|---|---|---|---|---|---|---|---|
| Capacity | kilolitre (kL) | hectolitre (hL) | decalitre (daL) | litre (L) | decilitre (dL) | centilitre (cL) | millilitre (mL) |
| Equivalent value in litres | 0.001 | 0.01 | 0.1 | 1 | 10 | 100 | 1 000 |
In this table, each unit is 10 times larger than the unit that follows it. So, 1 litre is 10 decilitres, 1 decilitre is 10 centilitres and so on.

Converting a unit of measure means changing the unit of measurement of a quantity to a smaller or larger unit.
The “jump” method or a metric conversion table can be used to convert from one unit of measurement to another.
According to this method, it is necessary to:
-
multiply the unit by 10 when going from a larger unit to a smaller unit
-
divide the unit by 10 when going from a smaller unit to a larger unit
Multiply or divide by 10 as many times as the number of positions moved.

For example, to go from cL to mL, multiply by 10. To go from mL to cL, divide by 10.
Generally, when moving to units to the right, multiply by 10 for each jump taken. When moving to units to the left, divide by 10 for each jump.
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 10}&=\text{centilitres}\\[4pt] 10\ \text{mL} &= 1\text{cL}\end{align}|
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 100}&=\text{decilitres}\\[4pt] 100\ \text{mL} &= 1\text{dL}\end{align}|
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 1\,000}&=\text{litres}\\[4pt] 1\,000\ \text{mL} &= 1\text{L}\end{align}|
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 1\,000\,000}&=\text{kilolitres}\\[4pt] 1\,000\,000\ \text{mL} &= 1\text{kL}\end{align}|
A metric conversion table can also be used to make conversions.
According to this method, it is necessary to:
-
Place the digit found in the ones position in the position of the given unit of measure. Place the other numbers (if there are any) to the left of it.
-
Put a 0 in each column up to the column of the new unit of measurement.
To convert 34 litres into centilitres, place the digit in the ones position in the litre column (the unit of measure of the starting number). Therefore, place the 4 in the litres column and the 3 in the decalitres column. Next, put 0’s in each column up to the centilitres column (the unit of measure sought).
This gives 3400 cL.

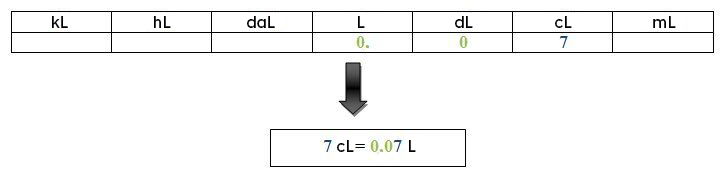
Convert 7 centilitres to litres. Place the digit 7 in the centilitres column (the unit of measure of the starting number). Next, put a 0 in each column up to the litres column (unit of measure sought). Finally, put a decimal point in the litres column.
The result is 0.07 L.
Units of capacity can be converted into units of volume. To do so, there are a number of important relationships to keep in mind:
||\begin{align}1\ \text{mL} &= 1\ \text{cm}^3\\ 1\ \text{L} &= 1\ \text{dm}^3\\ 1\ \text{kL} &= 1\ \text{m}^3\end{align}||
Convert |125\ \text{hL}| to |\text{hm}^3.|
-
Convert |\text{hL}| into one of the three known units (see previous box): |\text{kL},| |\text{L}| or |\text{mL}.| ||125\text{ hL}\times100 = 12\ 500 \text{L}||
-
Convert the litres into |\text{dm}^3.|
Since |1\text{ L} = 1\text{ dm}^3|:||12\ 500\text{ L} = 12\ 500\ \text{dm}^3|| -
Convert |\text{dm}^3| to |\text{hm}^3| ||12\ 500\div1000^3=0.0000125\text{ hm}^3||