La capacité est la mesure du volume qu'un récipient peut contenir. Par exemple, les contenants ci-dessous contiennent une certaine quantité de lait et de farine.

Dans la vie courante, on se sert de la capacité pour mesurer des quantités. Cette mesure est, entre autre, très utile en cuisine.
L'unité de mesure de base de la capacité est le litre (L).
Voici un tableau des unités les plus souvent utilisées :
| Préfixe | kilo- | hecto- | déca- | déci- | centi- | milli- | |
|---|---|---|---|---|---|---|---|
| Capacité | kilolitre (kL) | hectolitre (hL) | décalitre (daL) | litre (L) | décilitre (dL) | centilitre (cL) | millilitre (mL) |
| Valeur équivalente en litre | 0,001 | 0,01 | 0,1 | 1 | 10 | 100 | 1 000 |
Dans ce tableau, chaque unité est 10 fois plus grande que l'unité qui la suit. Ainsi, 1 litre vaut 10 décilitres, 1 décilitre vaut 10 centilitres, et ainsi de suite.
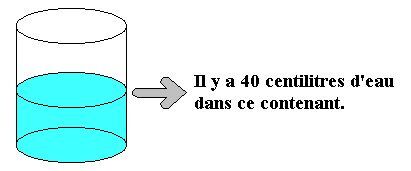
La conversion d'une unité de mesure consiste à exprimer une grandeur dans une unité de mesure inférieure ou supérieure.
On peut utiliser la méthode des bonds ou encore le tableau des unités de mesure pour convertir une mesure en une autre.
Selon cette méthode, il faut :
- multiplier l'unité par 10 lorsqu'on la transforme en une unité plus petite;
- diviser l'unité par 10 lorsqu'on la transforme en une unité plus grande.
Il faut multiplier ou diviser par 10 autant de fois qu'on se déplace de position.

Par exemple, pour passer de cL à mL, on doit multiplier par 10. Pour passer de mL à cL, on doit diviser par 10.
Généralement, quand on se déplace vers des unités situées vers la droite, on multiplie par 10 à chaque bond effectué. Quand on se déplace vers les unités situées vers la gauche, on divise par 10 à chaque bond effectué.
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 10}&=\text{centilitres}\\[4pt] 10\ \text{mL} &= 1\text{cL}\end{align}|
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 100}&=\text{décilitres}\\[4pt] 100\ \text{mL} &= 1\text{dL}\end{align}|
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 1\,000}&=\text{litres}\\[4pt] 1\,000\ \text{mL} &= 1\text{L}\end{align}|
-
|\begin{align}\text{Mililitres}\boldsymbol{\div 1\,000\,000}&=\text{kilolitres}\\[4pt] 1\,000\,000\ \text{mL} &= 1\text{kL}\end{align}|
On peut aussi utiliser un tableau pour faire les conversions.
Selon cette méthode, il faut :
- placer l'unité du nombre à la position de l'unité de mesure donnée et on place les autres nombres à gauche de celui-ci;
- mettre un 0 dans chaque colonne jusqu’à la colonne de l'unité de mesure recherchée.
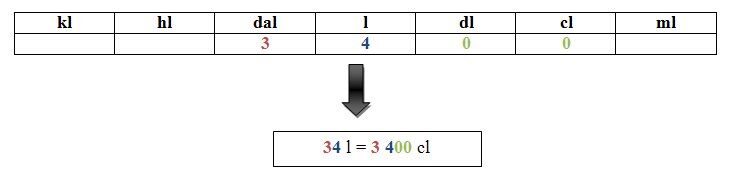
Si on veut convertir 34 litres en centilitres, on place le chiffre à la position de l’unité dans la colonne des litres (puisqu'il s'agit de l'unité de mesure du chiffre de départ). On place donc le 4 dans la colonne des litres et le 3 dans la colonne des décalitres. Ensuite, il ne reste plus qu’à mettre des 0 dans chaque colonne jusqu’à la colonne des centilitres (l'unité de mesure recherchée).
On obtient 3 400 cL.
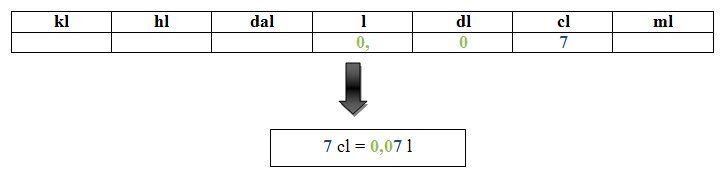
On veut convertir 7 centilitres en litres. On place le chiffre 7 dans la colonne des centilitres (unité de mesure de départ). On ajoute ensuite un 0 dans chaque colonne jusqu’à la colonne des litres (unité de mesure demandée). On ajoute finalement une virgule dans la colonne des litres.
On obtient 0,07 L.
Il est possible de transformer les unités de capacité en unités de volume. Pour cela, on doit retenir quelques relations importantes.
||\begin{align}1\ \text{mL} &= 1\ \text{cm}^3\\ 1\ \text{L} &= 1\ \text{dm}^3\\ 1\ \text{kL} &= 1\ \text{m}^3\end{align}||
On veut transformer |125\ \text{hL}| en |\text{hm}^3.|
-
On doit transformer les |\ \text{hL}| en l’une des trois unités connues (voir l'encadré précédent) : |\ \text{kL,}| |\text{L}| ou |\text{mL.}| ||125\ \text{hL} \times 100 = 12\ 500\ \text{L}||
-
On transforme les litres en |\ \text{dm}^3.|
Étant donné que |1\ \text{L} = 1\ \text{dm}^3,| on obtient : ||12\ 500\ \text{L} = 12\ 500\ \text{dm}^3|| -
On transforme les |\ \text{dm}^3| en |\ \text{hm}^3.| ||12\ 500\div1\ 000^3=0{,}000\,012\,5\ \text{hm}^3||