Length is the measurement of an object’s longest dimension (side).
In addition to being an object’s longest dimension, length is also used to physically measure the distance between two objects.
There are different units of measurement for length. Before 1971, the Imperial System was the official system used in Canada. This system’s units of measurement are feet, inches, and ounces, among others. However, since 1971 Canada has officially adopted the metric system, which is based on the metre.
The basic unit of measurement for length in the International System of Units (SI) is the metre (m).
The following is a table with the most commonly used units:
|
Prefix |
Kilo- |
Hecto- |
Deca- |
|
Deci- |
Centi- |
Milli- |
|---|---|---|---|---|---|---|---|
|
Longueur |
kilometre (km) |
hectometre (hm) |
Decametre (dam) |
Metre (m) |
Decimetre (dm) |
Centimetre (cm) |
Millimetre (mm) |
|
Equivalent value to 1 metre |
0.001 |
0.01 |
0.1 |
1 |
10 |
100 |
1 000 |
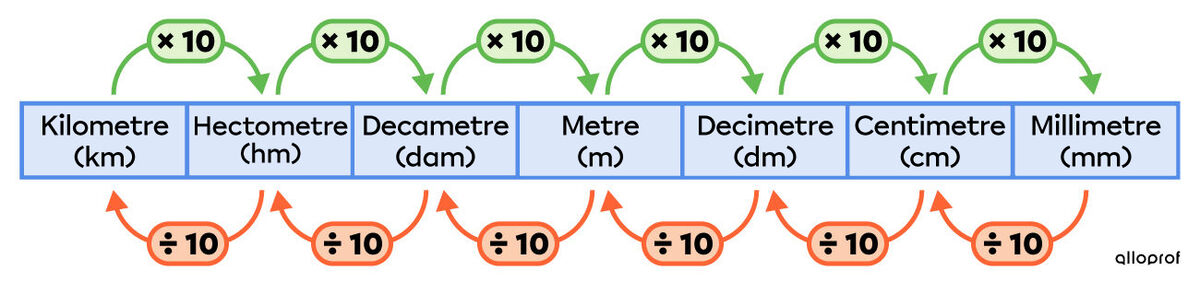
In the table, each unit is 10 times larger than the unit that follows it. Thus, 1 metre is equivalent to 10 decimetres, 1 decimetre is equivalent to 10 centimetres, etc.
-
Kilometres (km) are used to measure distances traveled by car.
-
Metres (m) are used to measure buildings.
-
Centimetres (cm) are used to measure everyday objects, such as a pencil or a desk.
-
Millimetres (mm) are used to measure very small objects.
Converting a unit of measurement involves expressing it using a smaller or larger unit of measurement.
The jump method or the metric conversion table can be used to convert one measurement to another.
The jump method or the metric conversion table can be used to convert one measurement to another.
When using this method, it is necessary to:
-
Multiply the unit by 10 when converting to a smaller unit;
-
Divide the unit by 10 when converting to a larger unit.
Multiply or divide by 10 based on the number of “jumps” made.
We want to convert 2.3 kilometres to metres.
To go from km to m, multiply by 10 each time the unit is changed.

|2{.}3\ \text{km}\times10 = 23\ \text{hm}|
|23\ \text{hm}\times10 = 230\ \text{dam}|
|230\ \text{dam}\times10 = 2\ 300\ \text{m}|
OR
|2{.}3\times10\times10\times10 = 2{.}3\times 1\ 000 = 2\ 300\ \text{m}|
Answer: |2{.}3\ \text{km} = 2\ 300\ \text{m}|
When using this method, it is necessary to:
-
Place the ones digit of the number in the position of the given unit of measurement. The other numbers are placed to the left of it.
-
Put a 0 in each column up to the column of the new unit of measurement.
We want to convert 34 metres to centimetres.
-
The number 4 is the ones digit of the number, so place it in the metres’ position in the table.
-
Place the 3 in the column to the left of the metres because it is to the left of the 4 in the starting number.
-
Put 0s in each column on the right, up to the centimetres column (since we want to convert to centimetres).
The number 3 400 is obtained. Thus, there are 3 400 cm in 34 m.

Converting from a smaller unit of measurement to a larger unit requires putting a decimal point in the column of the new unit of measurement.
We want to convert 17 millimetres to metres.
- The number 7 is the ones digit of the number, so place it in the millimetre’s position in the table.
-
Place the 1 in the column to the left of the millimetres because it is to the left of the 7 in the starting number.

-
Then add a 0 in each column up to the metres column (since we want to convert to metres).
-
Finally, add a decimal point in the metres column to the right of the 0. The number 0.017 is obtained. Thus, there are 0.017 metres in 17 millimetres.
