Momentum is a physical quantity of motion associated with the mass and speed of an object.
It is used to study the behavior of objects that collide with each other. As with energy, momentum must be the same at the beginning and end of a problem.
To determine the momentum of an object, the following equation must be used:
|\overrightarrow{p} = m \cdot \overrightarrow{v}|
where
|\overrightarrow{p}| represents the object's momentum |\text {kg}\cdot \text {m/s}|
|m| represents the mass of the object |\text {kg}|
|\overrightarrow{v}| represents the velocity of the object |\text {m/s}|
Collisions are classified into three categories.
An inelastic collision is a collision between two objects in which the momentum is conserved, but the kinetic energy is not.
A perfectly inelastic collision is one in which the two objects remain attached to each other.
An elastic collision is a collision between two objects in which both the momentum and kinetic energy are conserved.
A cannon on wheels that weighs |2000 \: \text {kg}| fires a |25 \: \text {kg}| ball to the right. If the barrel recoils at a rate of |2 \: \text {m/s}| (to the left), what is the speed of the cannonball?
Horizontally, the sum of the momentums at the start must equal those at the end.
||\begin{align}
\overrightarrow{p}_{\text{canon}_{i}}+\overrightarrow{p}_{\text{cannonball}_{i}}&=\overrightarrow{p}_{\text{canon}_{f}}+\overrightarrow{p}_{\text{cannonball}_{f}} \\
m \cdot \overrightarrow{v}_{\text{canon}_{i}}+m \cdot \overrightarrow{v}_{\text{cannonball}_{i}}&=m \cdot \overrightarrow{v}_{\text{canon}_{f}}+m \cdot \overrightarrow{v}_{\text{cannonball}_{f}} \\
2000 \: \text {kg} \cdot 0 \: \text {m/s} + 25 \: \text {kg} \cdot 0 \: \text {m/s} &= 2000 \: \text {kg} \cdot (-2 \: \text {m/s}) + 25 \: \text {kg} \cdot \overrightarrow{v}_{cannonball_{f}} \\
0 &= - 4000 + 25 \cdot \overrightarrow{v}_{cannonball_{f}} \\
4000 &= 25 \cdot \overrightarrow{v}_{cannonball_{f}} \\
\overrightarrow{v}_{cannonball_{f}} &= + 160 \: \text {m/s}
\end{align}||
The impulse represents the momentum (or quantity of motion) transmitted to an object.
To change the momentum of an object, a force must be applied to it over a certain period of time.
The equation for determining the impulse is as follows:
|\overrightarrow{J}=\overrightarrow{F} \cdot \triangle t |
where
|\overrightarrow{J}| represents the transmitted impulse |\text {N} \cdot \text {s}|
|\overrightarrow{F}| represents the net force acting on an object |\text {N}|
|\triangle t | represents the elapsed time |\text {s}|
Impulse can also be calculated by determining the area under the curve of a graph that represents force in relation to the time elapsed.
The force applied to a sled is represented on the graph below. What impulse has been applied to the sled?
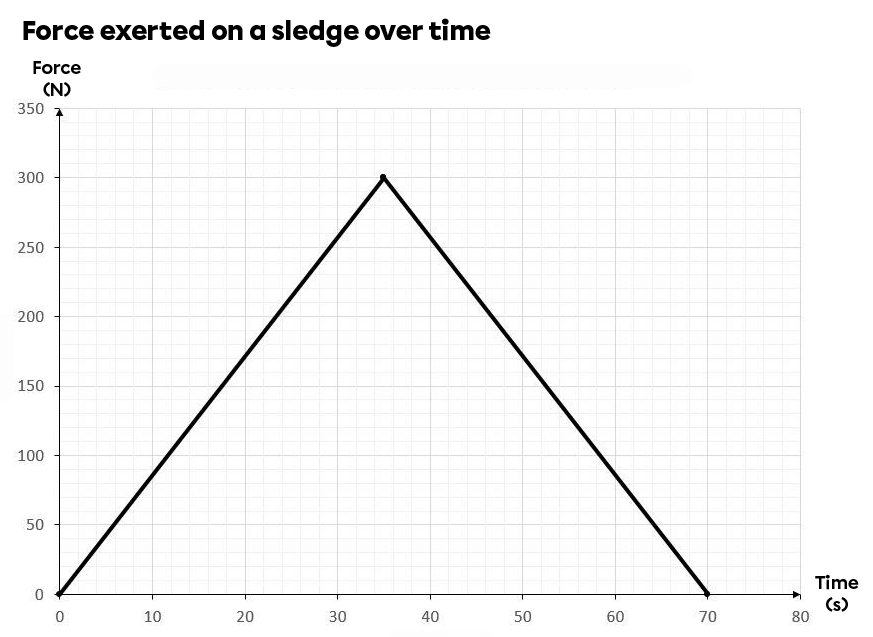
To calculate the impulse, you need to calculate the area under the curve.
||\begin{align}A = \frac {b \times h}{2} \quad \Rightarrow \quad A &= \frac {70 \: \text {s} \times 300 \: \text {N}}{2} \\
&= 10 \: 500 \: \text {N} \cdot \text {s}
\end{align}||
Since the impulse varies the momentum, it is possible to link these two variables using a formula.
The relationship between impulse and momentum is described by the following equation:
|\overrightarrow{I}=\overrightarrow{p}_{f} - \overrightarrow{p}_{i}|
where
|\overrightarrow{I}| represents the impulse |\text {N} \cdot \text {s}|
|\overrightarrow{p}_{f}| represents the final momentum |\text {kg} \cdot \text {m/s}|
|\overrightarrow{p}_{i}| represents the initial momentum |\text {kg} \cdot \text {m/s}|
Since both of these quantities of motion (momentum and impulse) are vectors in the previous equation, we will need to subtract the vectors to find the impulse. However, when these two quantities of motion are oriented in the same direction, we can just subtract their vector magnitudes.