La quantité de mouvement est une grandeur physique qui est associée à la masse et à la vitesse d’un objet.
On l’utilise pour étudier le comportement des objets qui entrent en collision les uns avec les autres. Tout comme l’énergie, la quantité de mouvement doit être la même au début et à la fin d’un problème.
Pour déterminer la quantité de mouvement d’un objet, on doit utiliser l’équation suivante :
|\overrightarrow{p} = m \cdot \overrightarrow{v}|
où
|\overrightarrow{p}| représente la quantité de mouvement de l'objet |\small (\text {kg}\cdot \text {m/s})|
|m| représente la masse de l'objet |\small (\text {kg})|
|\overrightarrow{v}| représente la vitesse de l'objet |\small (\text {m/s})|
On classe les collisions en trois catégories.
Une collision inélastique est une collision entre deux objets au cours de laquelle la quantité de mouvement est conservée, mais où l’énergie cinétique ne l’est pas.
Une collision parfaitement inélastique est une collision inélastique à la suite de laquelle deux objets restent accrochés.
Une collision élastique est une collision entre deux objets au cours de laquelle la quantité de mouvement et l’énergie cinétique sont conservées.
Un canon sur roulettes dont la masse est de |\small 2 \: 000 \: \text {kg}| tire un boulet de |\small 25 \: \text {kg}| vers la droite. Si le canon a une vitesse de recul de |\small 2 \: \text {m/s}| (vers la gauche), quelle est la vitesse du boulet?
Horizontalement, la somme des quantités de mouvement au départ doit être égale aux quantités de mouvement à la fin.
||\begin{align}
\overrightarrow{p}_{\text{canon}_{i}}+\overrightarrow{p}_{\text{boulet}_{i}}&=\overrightarrow{p}_{\text{canon}_{f}}+\overrightarrow{p}_{\text{boulet}_{f}} \\
m \cdot \overrightarrow{v}_{\text{canon}_{i}}+m \cdot \overrightarrow{v}_{\text{boulet}_{i}}&=m \cdot \overrightarrow{v}_{\text{canon}_{f}}+m \cdot \overrightarrow{v}_{\text{boulet}_{f}} \\
2000 \: \text {kg} \cdot 0 \: \text {m/s} + 25 \: \text {kg} \cdot 0 \: \text {m/s} &= 2000 \: \text {kg} \cdot (-2 \: \text {m/s}) + 25 \: \text {kg} \cdot \overrightarrow{v}_{boulet_{f}} \\
0 &= - 4000 + 25 \cdot \overrightarrow{v}_{boulet_{f}} \\
4000 &= 25 \cdot \overrightarrow{v}_{boulet_{f}} \\
\overrightarrow{v}_{boulet_{f}} &= + 160 \: \text {m/s}
\end{align}||
L’impulsion représente la quantité de mouvement transmise à un objet.
Pour modifier la quantité de mouvement d’un objet, on doit lui appliquer une force pendant un certain temps.
L’équation pour déterminer l’impulsion est la suivante:
|\overrightarrow{J}=\overrightarrow{F} \cdot \triangle t |
où
|\overrightarrow{J}| représente l'impulsion transmise |\small (\text {N} \cdot \text {s})|
|\overrightarrow{F}| représente la force |\small (\text {N})|
|\triangle t | représente le temps |\small (\text {s})|
L’impulsion peut aussi être calculée en déterminant l’aire sous la courbe d’un graphique de la force en fonction du temps.
La force appliquée à un traîneau est représentée sur le graphique ci-dessous. Quelle impulsion lui a-t-on transmise ?
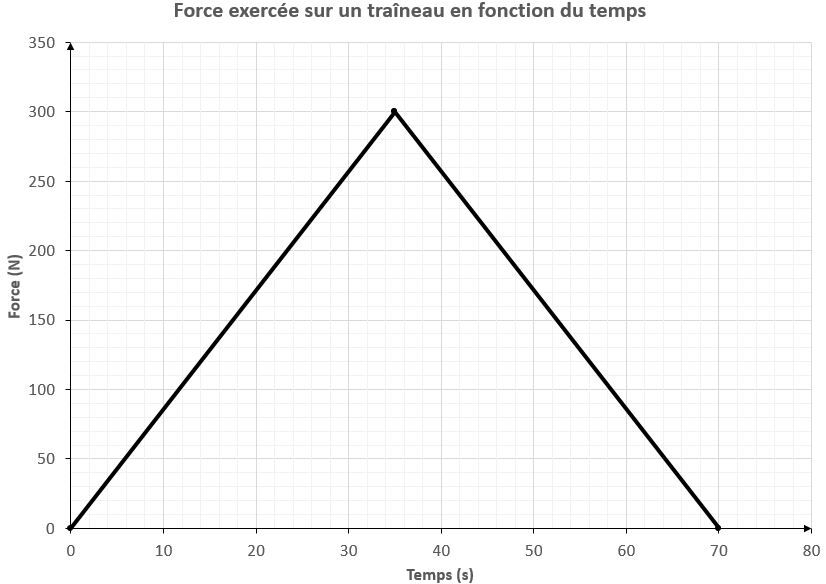
Pour calculer l'impulsion, il faut calculer l'aire sous la courbe.
||\begin{align}A = \frac {b \times h}{2} \quad \Rightarrow \quad A &= \frac {70 \: \text {s} \times 300 \: \text {N}}{2} \\
&= 10 \: 500 \: \text {N} \cdot \text {s}
\end{align}||
Puisque l’impulsion aura pour effet de faire varier la quantité de mouvement, il est possible de faire un lien entre ces deux variables par une formule.
La relation entre l'impulsion et la quantité de mouvement est décrite par la relation suivante:
|\overrightarrow{I}=\overrightarrow{p}_{f} - \overrightarrow{p}_{i}|
où
|\overrightarrow{I}| représente l'impulsion |\small (\text {N} \cdot \text {s})|
|\overrightarrow{p}_{f}| représente la quantité de mouvement final |\small (\text {kg} \cdot \text {m/s})|
|\overrightarrow{p}_{i}| représente la quantité de mouvement initial |\small (\text {kg} \cdot \text {m/s})|
Comme les quantités de mouvement sont vectorielles dans l’équation précédente, il faudra faire une soustraction vectorielle pour déterminer l’impulsion. Par contre, lorsque les deux quantités de mouvement ont la même orientation, il est possible de ne soustraire que les grandeurs des vecteurs.