Centripetal force is the force that holds an object in circular motion.
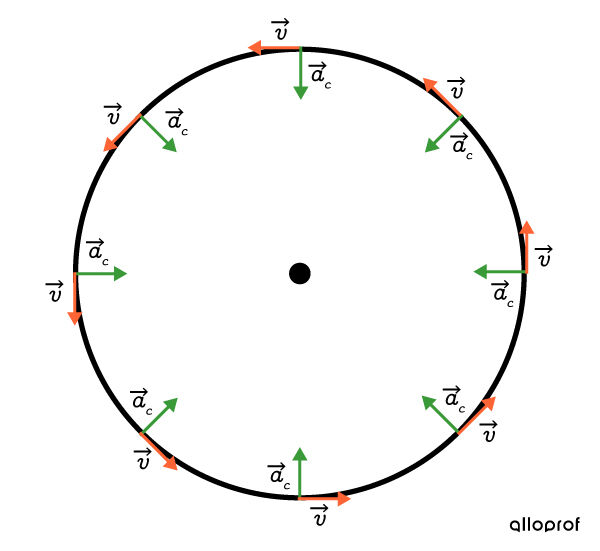
Centripetal acceleration is the acceleration that causes the velocity vector to change orientation in a situation of uniform circular motion.
In uniform circular motion, the velocity is constant. However, unlike rectilinear motion (whether MRU or MRUA), the orientation is constantly changing. There is therefore an acceleration (|\overrightarrow{a_c}|), and this acceleration is perpendicular to the velocity (|\overrightarrow{v}|).
Take the example of a weight attached to a rope.
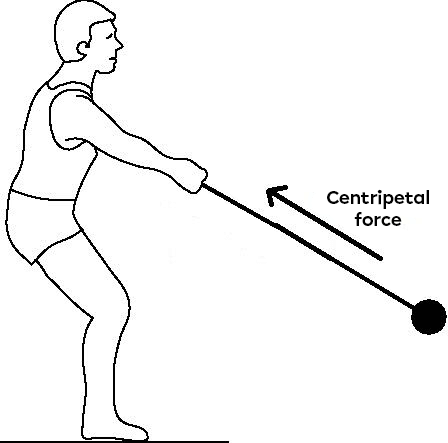
If the person starts to turn on themselves while holding the rope, the centripetal force is directed towards the centre of rotation, i.e. the person. This force will keep the weight in a circular motion. If the person lets go of the rope, the centripetal force will disappear and the weight will move in a straight line.
To determine the centripetal acceleration, use the following formula:
|a_{c} = \displaystyle \frac {v^{2}}{r}|
where
|a_{c}| represents the centripetal acceleration |\small (\text {m/s}^2)|
|v| represents the speed of rotation of the object |\small (\text {m/s})|
|r| represents the radius of the circle in metres |\small (\text {m})|
To determine the centripetal force, we need to use Newton's second law and substitute the acceleration by the formula described above.
To determine the centripetal force, use the following formula:
|F_{c} = m \times \displaystyle \frac {v^{2}}{r}|
where
|F_{c}| represents the centripetal force in Newtons |\small (\text {N})|
|m| represents the mass in kilograms |\small (\text {kg})|
|v| represents the speed of rotation of the object in metres per second |\small (\text {m/s})|
|r| represents the radius of the circle in metres |\small (\text {m})|
The centripetal force is always in the same direction as the centripetal acceleration, i.e. towards the centre of the circle representing the trajectory of the moving object.
In a merry-go-round, the vertical loop has a radius of |\small \text {10 m}|. The train, with a mass of |\small \text {500 kg}|, maintains a speed of |\small \text {54 km/h}|. What is the magnitude of the centripetal force?
Here is the known information in this example.
||\begin{align}r &= 10 \: \text {m} &m &= 500 \: \text {kg}\\
v &= 54 \: \text {km/h} = 15 \: \text {m/s} \end{align}||
The centripetal force is determined using the formula above.
||\begin{align} F_{c} = m \times \displaystyle \frac {v^{2}}{r}
\quad \Rightarrow \quad
\text {F}_{c} &= 500 \: \text{kg} \times \frac {(15 \: \text {m/s})^{2}}{(10 \: \text{m})} \\
&= 11\:250 \: \text {N} \end{align}||
Centrifugal force is the fictitious force that causes a body to move away from the centre of rotation of a circular movement.
When a car enters a sharp bend, it exerts a force towards the inside of the bend in order to bring the car in the appropriate direction - the centripetal force. However, when the car turns, the people sitting inside the car feel a force that tends to pull them outwards, as if they were being pushed in the opposite direction to the curve. This force is known as centrifugal force.
The same principle applies to certain high-speed merry-go-rounds. A person on such a ride will not be pulled towards the centre, but rather compressed in their seat as they feel the effects of centrifugal force. This force causes them to remain in their seat rather than continue moving in a straight line.