La force centripète est la force qui maintient un objet dans un mouvement circulaire.
L'accélération centripète est l'accélération qui provoque le changement d'orientation du vecteur vitesse dans une situation de mouvement circulaire uniforme.
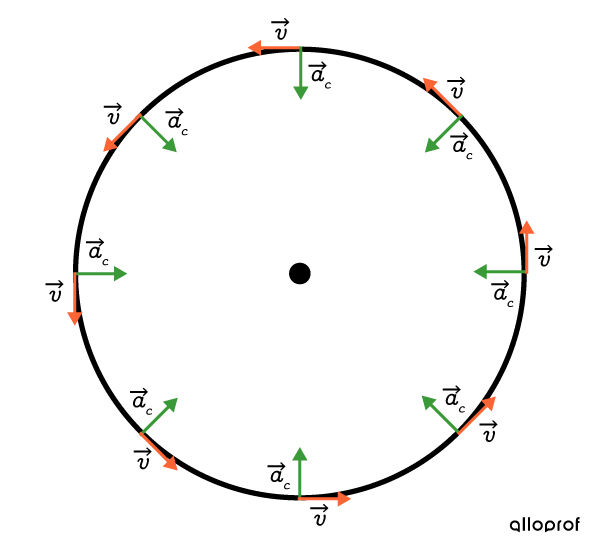
Dans un mouvement circulaire uniforme, la vitesse est constante. Toutefois, contrairement aux mouvements rectilignes (que ce soit le MRU ou le MRUA), l'orientation change constamment. Il y a donc une accélération (|\overrightarrow{a_c}|), et cette accélération est perpendiculaire à la vitesse (|\overrightarrow{v}|).
On peut prendre l'exemple d'un poids attaché à une corde.
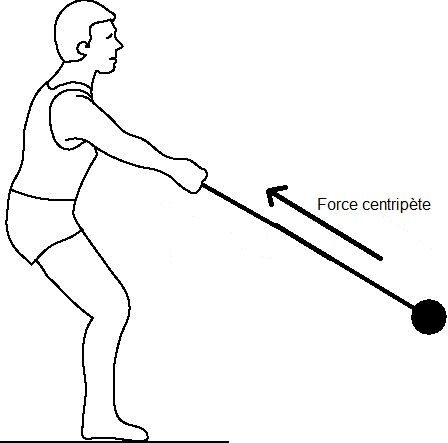
Si la personne se met à tourner sur elle-même en tenant la corde, la force centripète est dirigée vers le centre de rotation, soit la personne. Cette force maintiendra le poids dans un mouvement circulaire. Si la personne lâche la corde, la force centripète disparaîtra et le poids se déplacera dans une trajectoire rectiligne.
Pour déterminer l'accélération centripète, il faut utiliser la formule suivante:
|a_{c} = \displaystyle \frac {v^{2}}{r}|
où
|a_{c}| représente l'accélération centripète |\small (\text {m/s}^2)|
|v| représente la vitesse de rotation de l'objet |\small (\text {m/s})|
|r| représente le rayon du cercle en mètres |\small (\text {m})|
Pour déterminer la force centripète, il faut utiliser la deuxième loi de Newton et substituer l'accélération par la formule décrite ci-dessus.
Pour déterminer la force centripète, il faut utiliser la formule suivante:
|F_{c} = m \times \displaystyle \frac {v^{2}}{r}|
où
|F_{c}| représente la force centripète en Newtons |\small (\text {N})|
|m| représente la masse en kilogrammes |\small (\text {kg})|
|v| représente la vitesse de rotation de l'objet en mètres par seconde |\small (\text {m/s})|
|r| représente le rayon du cercle en mètres |\small (\text {m})|
La force centripète est toujours orientée dans le même sens que l'accélération centripète, soit vers le centre du cercle représentant la trajectoire de l'objet en mouvement.
Dans un manège, la boucle verticale possède un rayon de |\small \text {10 m}|. Le train, ayant une masse de |\small \text {500 kg}|, maintient une vitesse de |\small \text {54 km/h}|. Quelle est la grandeur de la force centripète?
Voici les informations connues dans cet exemple.
||\begin{align}r &= 10 \: \text {m} &m &= 500 \: \text {kg}\\
v &= 54 \: \text {km/h} = 15 \: \text {m/s} \end{align}||
On détermine la force centripète en utilisant la formule ci-dessus.
||\begin{align} F_{c} = m \times \displaystyle \frac {v^{2}}{r}
\quad \Rightarrow \quad
\text {F}_{c} &= 500 \: \text{kg} \times \frac {(15 \: \text {m/s})^{2}}{(10 \: \text{m})} \\
&= 11\:250 \: \text {N} \end{align}||
La force centrifuge est la force fictive qui amène un corps à s'éloigner du centre de rotation d'un mouvement circulaire.
Lorsqu'une voiture entre dans une courbe prononcée, elle exerce une force vers l'intérieur du virage afin d'amener la voiture dans la direction appropriée, soit la force centripète. Or, quand la voiture tourne, les personnes assises à l'intérieur de la voiture ressentent une force qui tend à les amener vers l'extérieur, comme si elles devaient être déportées dans le sens contraire de la courbe. C'est cette force que l'on nomme force centrifuge.
Le même principe existe dans certains manèges tournant à grande vitesse. Pour une personne située dans ce manège, elle ne sera pas attirée vers le centre, mais plutôt comprimée sur son siège, car elle ressent les effets de la force centrifuge. Cette force l'amène à rester assise sur son siège plutôt que de continuer son mouvement en ligne droite.