The normal force is the force exerted on an object by a surface in contact with it.
The normal force represents the reaction force (action-reaction principle) of a surface preventing an object from sinking into it.
The normal force must always be perpendicular to the surface.
As shown in the image below, the force of gravity should normally pull the object towards the ground (or towards the centre of the Earth). However, the table keeps the object stationary by exerting an upward force that cancels out the force of gravity. This force exerted by the table is called the normal force.
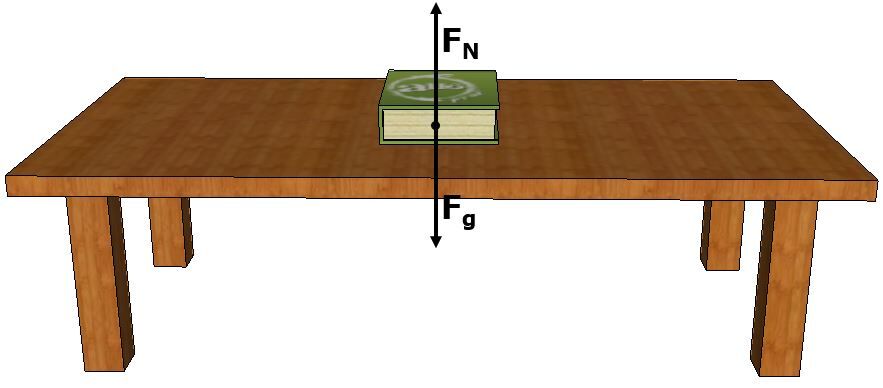
In the case of a flat surface (like the book and table above), the normal force is generally equal to the gravitational force. However, if an additional force were applied to the book (for example, if the book were pushed onto the table), the normal force would increase.
To determine the normal force on an inclined plane, we use the following formula:
|F_{N} = m \times g \times \cos \theta|
where
|F_{N}| is the normal force |\small (\text {N})|
|m| represents the mass of the objectt |\small (\text {kg})|
|g| represents the gravitational acceleration |\small (\text {N/kg or m/s}^2)|
|\theta| is the angle of inclination |\small (^{\circ})|
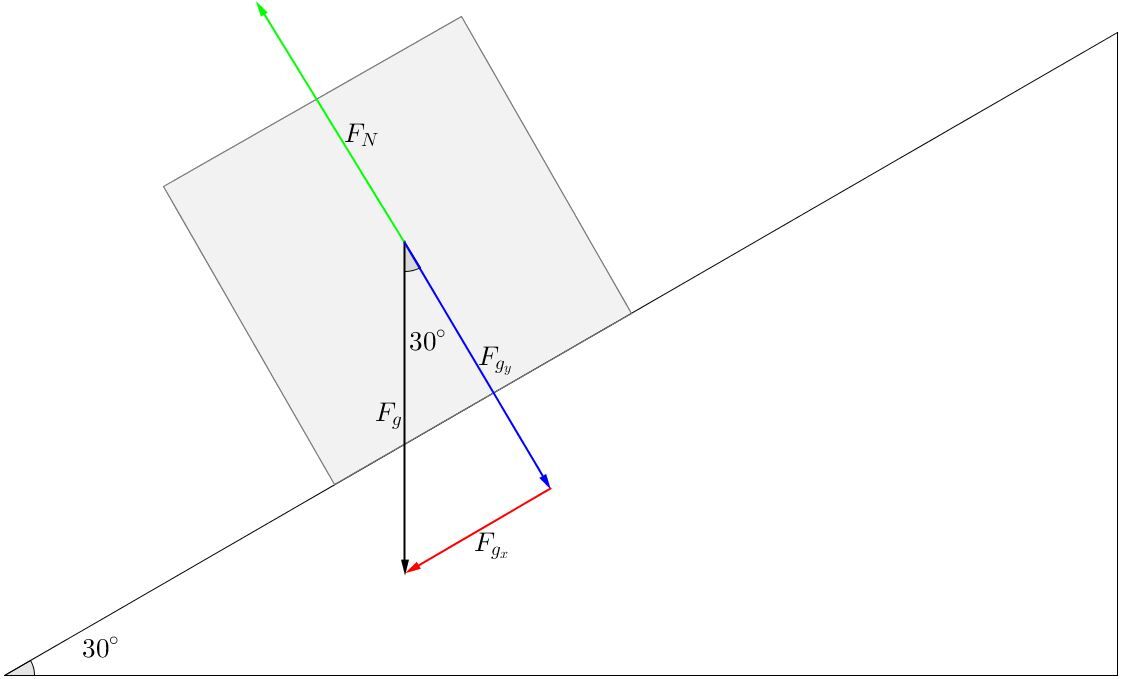
The normal force must always be perpendicular to the surface. However, when the surface is inclined, the normal force is not equal to the gravitational force, but rather to the component of the gravitational force that is perpendicular to the surface (shown in blue in the diagram below). The normal force (shown in green in the diagram below) will be of the same magnitude, but in the opposite direction to this component.
What is the normal force of a block of |\small 10 \: \text {kg}| placed on a plane inclined at |\small 30 ^{\circ}| ?
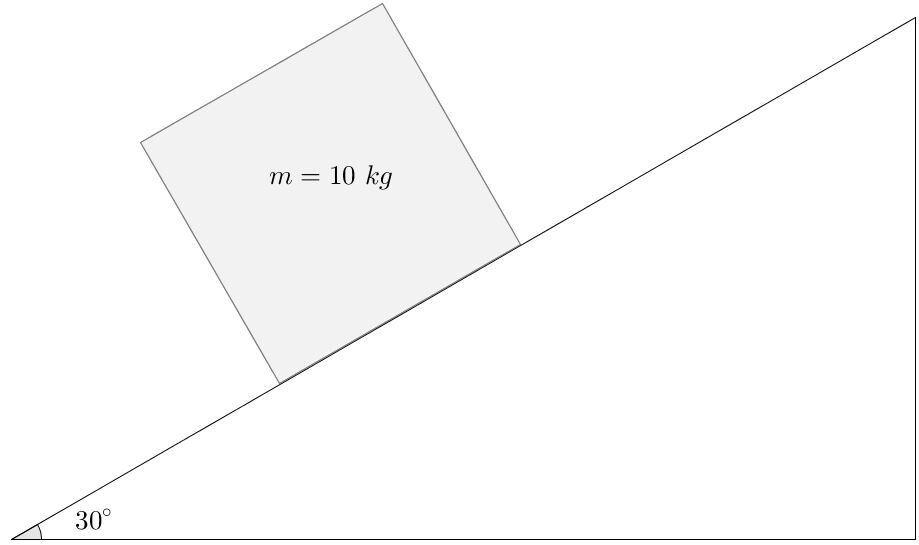
Here is the information known in this example.
||\begin{align} g &= 9.8 \: \text {N/kg} &m &= 10 \: \text {kg}\\
\theta &= 30^{\circ} \end{align}||
Using the formula for calculating the normal force on an inclined plane, the response can be determined.
||\begin{align} F_{N} = m \times g \times \cos \theta
\quad \Rightarrow \quad
{F}_{N} &= 10 \: \text {kg} \times 9.8 \: \text {N/kg} \times \cos 30^{\circ} \\
&= 84.9 \: \text {N} \end{align}||
The normal force is therefore |84.9\ \text {N}|.