La force normale est la force exercée sur un objet par une surface en contact avec celui-ci.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>La force normale représente la force de réaction (<a href="/fr/eleves/bv/physique/les-lois-de-newton-p1014">principe d’action-réaction</a>) d’une surface empêchant un objet de s’enfoncer dans cette surface.</p>
</body></html>
La force normale doit toujours être perpendiculaire à la surface.
Comme l'illustre l’image ci-dessous, la force de gravité devrait normalement amener l’objet vers le sol (ou vers le centre de la Terre). Toutefois, la table garde l’objet immobile en exerçant une force vers le haut qui vient annuler la force de gravité. Cette force exercée par la table est appelée force normale.
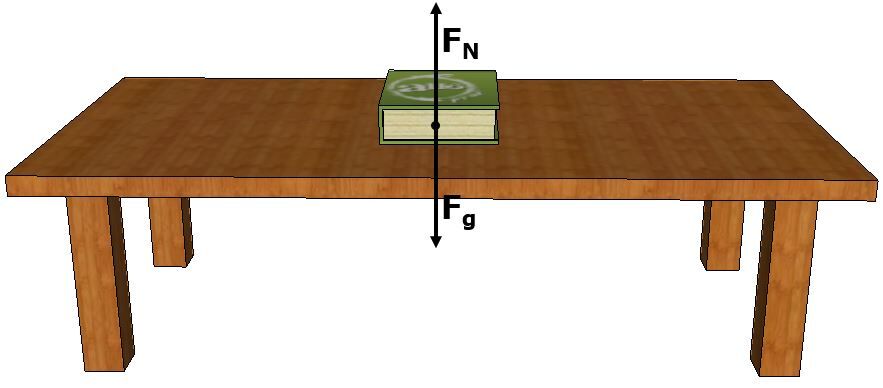
Dans le cas d'une surface plane (comme le livre et la table ci-dessus), la force normale est généralement égale à la force gravitationnelle. Toutefois, si une force supplémentaire était appliquée sur le livre (par exemple, si on poussait le livre sur la table), la force normale augmenterait.
Pour déterminer la force normale sur un plan incliné, on utilise la formule suivante:
|F_{N} = m \times g \times \cos \theta|
où
|F_{N}| représente la force normale |\small (\text {N})|
|m| représente la masse de l'objet |\small (\text {kg})|
|g| représente l'accélération gravitationnelle |\small (\text {N/kg ou m/s}^2)|
|\theta| représente l'angle d'inclinaison |\small (^{\circ})|
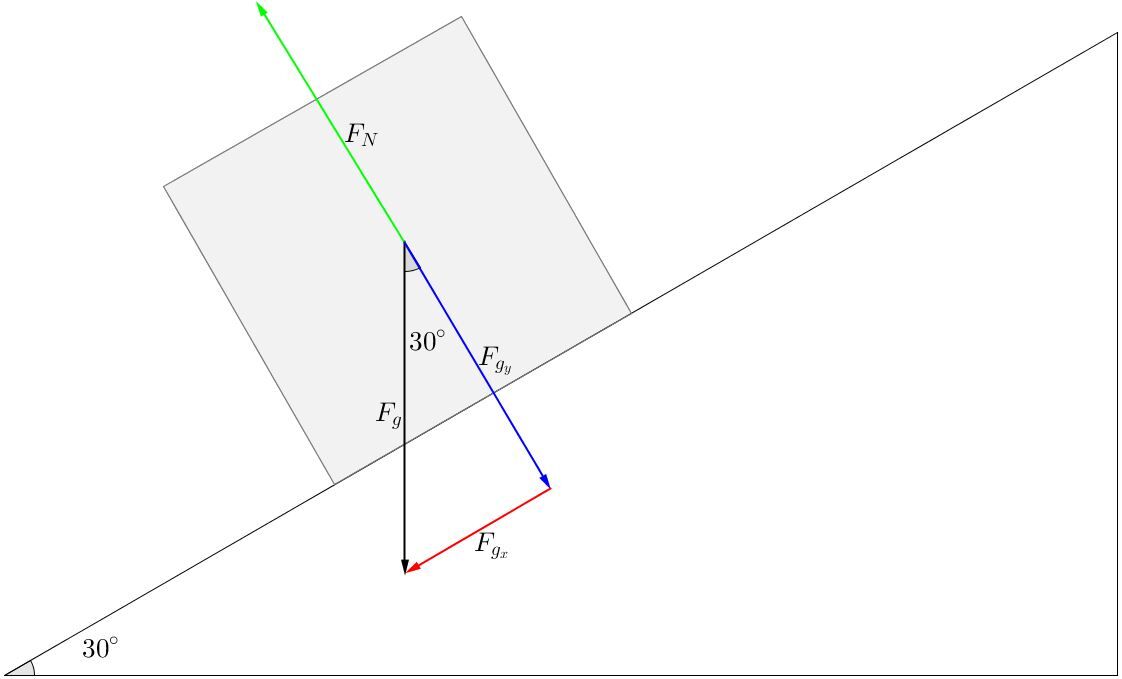
La force normale doit toujours être perpendiculaire à la surface. Or, lorsque la surface est inclinée, la force normale n'est pas égale à la force gravitationnelle, mais plutôt à la composante de la force gravitationnelle qui est perpendiculaire à la surface (représentée en bleu dans le schéma ci-dessous). La force normale (représentée en vert su le schéma ci-dessous) sera de la même grandeur, mais de sens opposé à cette composante.
Quelle est la force normale d'un bloc de |\small 10 \: \text {kg}| placé sur un plan incliné à |\small 30 ^{\circ}| ?
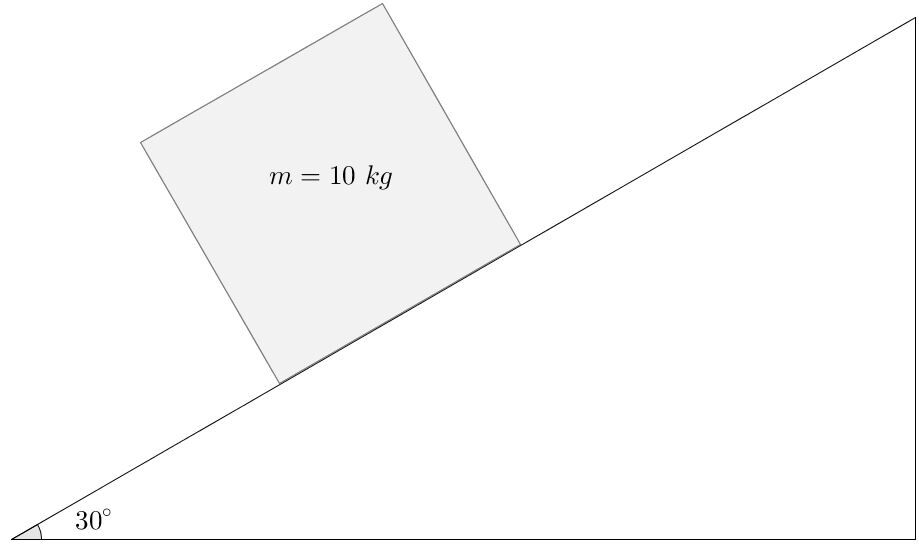
Voici les informations connues dans cet exemple.
||\begin{align} g &= 9,8 \: \text {N/kg} &m &= 10 \: \text {kg}\\
\theta &= 30^{\circ} \end{align}||
En utilisant la formule permettant de calculer la force normale sur un plan incliné, la réponse pourra être déterminée.
||\begin{align} F_{N} = m \times g \times \cos \theta
\quad \Rightarrow \quad
{F}_{N} &= 10 \: \text {kg} \times 9,8 \: \text {N/kg} \times \cos 30^{\circ} \\
&= 84,9 \: \text {N} \end{align}||
La force normale est donc |84,9 \text {N}|.